关于dijkstra求最短路(模板）

嗯....

 

dijkstra是求最短路的一种算法（废话，思维含量较低，

 

并且时间复杂度较为稳定，为O(n^2),

 

但是注意：！！！！         不能处理边权为负的情况（但SPFA可以处理，今后会讲)

 

借一个何大佬的图，因为会在代码中提到红、绿、空三种颜色，以及小v，

 

通过图会比较清晰一些：

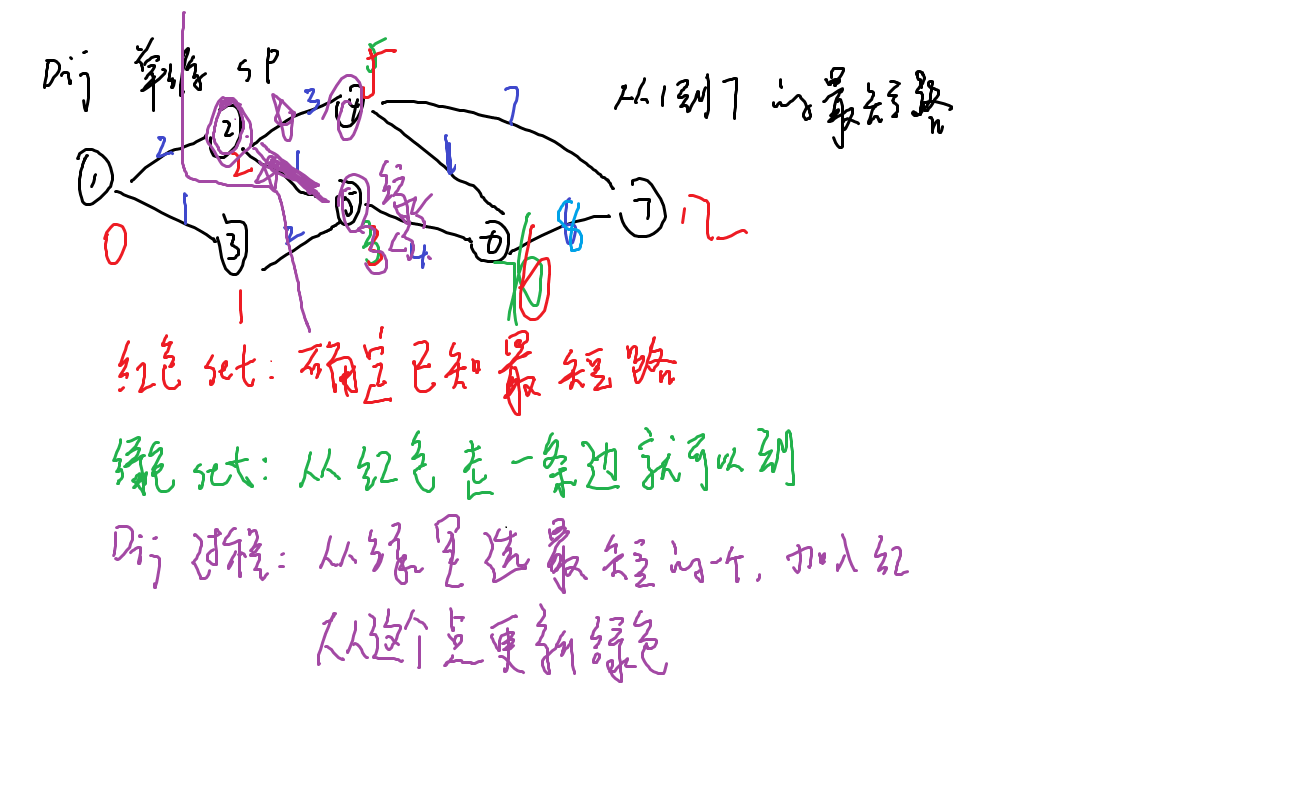
思路大约明白了下面就呈上带批注模板代码：

 #include <cstdio>//dijkstra求最短路
 #include <cstring>
 #include <algorithm>
 using namespace std;
 ;
 int g[maxn][maxn], n, m;//g数组用来存图
 int dis[maxn], status[maxn];//dis数组中存储的是从起点到第i个点的最短路长度 

 /*status//(状态)用来存点的类型，1.已经求出最短路的点(把它想成红色，用2来表示)
 2.是从已经求出最短路的点向外延伸一次就可找到的点(把它想成绿色，用1来表示)
 3.其余还没有访问的，仍没有色(用0来表示)*/ 

 //注意每一种算法都要新开一个函数，使代码简单易懂
 void dijkstra(int start_point) {//dijkstra 最短路写法：
     memset(dis, 0x3f, sizeof(dis));//将dis数组中的每一个元素都设为正无穷，
     //因为后面要用它与更小的最短路进行比较，所以它为最大，且定义为正无穷
     dis[start_point] = ;//确定边界，起点的最短路一定为0
     status[start_point] = ;//起点已求出最短路，首先标记为绿色，进行分析
     ; ti < n; ++ti) //枚举n次
     {
         ;//将小V初始化为-1(小V即为要找的点)
         ; i <= n; ++i) //再次进行枚举
         {
             ) //如果i点为绿色
             {
                  || dis[i] < dis[vertex_to_pick])
                 //如果v还没有被更新或者说是找到一个点i比点v到出发点的距离更近，则也进行更新
                  {
                     vertex_to_pick = i;//进行更新
                 }
             }
         }
         ) {
             break;//如果找不到下一个点，则退出
         }
         status[vertex_to_pick] = ;//将已经更新好的最近的v添加到red集合
         ; i <= n; ++i)
         //从找到的v点进行更新dis数组
         {
              || status[i] == ) //如果i点还没有添加到red集合
             {
                 )// 并且满足从小v这个点到i点有距离
                 {
                     status[i] = ;//再次将i点加入绿色集合，进行循环，找到所有相邻点
                     dis[i] = min(dis[i], dis[vertex_to_pick] + g[vertex_to_pick][i]);//更新i点的最短路
                 }
             }
         }
     }
 }

 int main() {
     //主函数进行输入、调用、输出
     memset(g, -, sizeof(g));
     scanf("%d%d", &n, &m);
     ; i < m; ++i) {
         int u, v, w;
         scanf("%d%d%d", &u, &v, &w);
         g[u][v] = g[v][u] = w;
     }
     dijkstra();
     printf("%d",dis[n]);
     ;
 }

多背几遍应该能明白，   反正一直除了更新就是更新.....