POJ 1265 Area (Pick定理 & 多边形面积)

题目链接：POJ 1265

Problem Description

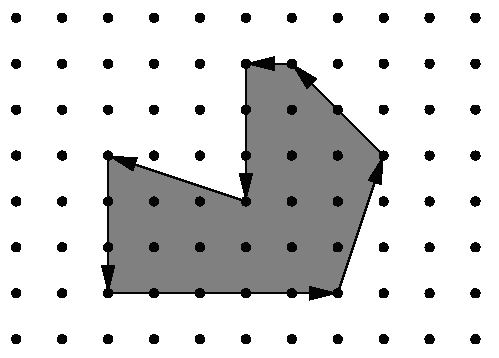
Being well known for its highly innovative products, Merck would definitely be a good target for industrial espionage. To protect its brand-new research and development facility the company has installed the latest system of surveillance robots patrolling the area. These robots move along the walls of the facility and report suspicious observations to the central security office. The only flaw in the system a competitor抯 agent could find is the fact that the robots radio their movements unencrypted. Not being able to find out more, the agent wants to use that information to calculate the exact size of the area occupied by the new facility. It is public knowledge that all the corners of the building are situated on a rectangular grid and that only straight walls are used. Figure 1 shows the course of a robot around an example area.

Figure 1: Example area.

You are hired to write a program that calculates the area occupied by the new facility from the movements of a robot along its walls. You can assume that this area is a polygon with corners on a rectangular grid. However, your boss insists that you use a formula he is so proud to have found somewhere. The formula relates the number I of grid points inside the polygon, the number E of grid points on the edges, and the total area A of the polygon. Unfortunately, you have lost the sheet on which he had written down that simple formula for you, so your first task is to find the formula yourself.

Input

The first line contains the number of scenarios.

For each scenario, you are given the number m, 3 <= m < 100, of movements of the robot in the first line. The following m lines contain pairs 揹x dy�of integers, separated by a single blank, satisfying .-100 <= dx, dy <= 100 and (dx, dy) != (0, 0). Such a pair means that the robot moves on to a grid point dx units to the right and dy units upwards on the grid (with respect to the current position). You can assume that the curve along which the robot moves is closed and that it does not intersect or even touch itself except for the start and end points. The robot moves anti-clockwise around the building, so the area to be calculated lies to the left of the curve. It is known in advance that the whole polygon would fit into a square on the grid with a side length of 100 units.

Output

The output for every scenario begins with a line containing 揝cenario #i:� where i is the number of the scenario starting at 1. Then print a single line containing I, E, and A, the area A rounded to one digit after the decimal point. Separate the three numbers by two single blanks. Terminate the output for the scenario with a blank line.

Sample Input

2
4
1 0
0 1
-1 0
0 -1
7
5 0
1 3
-2 2
-1 0
0 -3
-3 1
0 -3

Sample Output

Scenario #1:
0 4 1.0

Scenario #2:
12 16 19.0

Source

Northwestern Europe 2001

Solution

题意

给定一个多边形，所有点都在格点上，求多边形内部的点，边上的点和多边形的面积。

思路

Pick定理

Pick 定理：多边形面积 \(A\) 和内部格点数目 \(i\)，边上格点数目 \(b\) 的关系为 \(A = i + \frac{b}{2} - 1\) 。

相关证明见 Pick's theorem

多边形面积：按顺序求相邻两点与原点组成的向量的向量的叉积之和。

多边形边上的点：若一条边的两个点都在格点上，则该边上的格点数为 \(gcd(dx, dy)\)，\(dx\) 和 \(dy\) 分别为线段横向占的点数和纵向占的点数。

Code

#include <cstdio>
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef double db;
const db eps = 1e-10;
const db pi = acos(-1.0);
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll maxn = 1e5 + 10;

inline int dcmp(db x) {
    if(fabs(x) < eps) return 0;
    return x > 0? 1: -1;
}

class Point {
public:
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    void input() {
        scanf("%lf%lf", &x, &y);
    }
    bool operator<(const Point &a) const {
        return (!dcmp(x - a.x))? dcmp(y - a.y) < 0: x < a.x;
    }
    bool operator==(const Point &a) const {
        return dcmp(x - a.x) == 0 && dcmp(y - a.y) == 0;
    }
    db dis2(const Point a) {
        return pow(x - a.x, 2) + pow(y - a.y, 2);
    }
    db dis(const Point a) {
        return sqrt(dis2(a));
    }
    db dis2() {
        return x * x + y * y;
    }
    db dis() {
        return sqrt(dis2());
    }
    Point operator+(const Point a) {
        return Point(x + a.x, y + a.y);
    }
    Point operator-(const Point a) {
        return Point(x - a.x, y - a.y);
    }
    Point operator*(double p) {
        return Point(x * p, y * p);
    }
    Point operator/(double p) {
        return Point(x / p, y / p);
    }
    db dot(const Point a) {
        return x * a.x + y * a.y;
    }
    db cross(const Point a) {
        return x * a.y - y * a.x;
    }
};

Point p[110];

int gcd(int a, int b) {
    return b == 0? a: gcd(b, a % b);
}

int main() {
    int T;
    scanf("%d", &T);
    for(int _ = 1; _ <= T; ++_) {
        int n;
        scanf("%d", &n);
        int on = 0;
        db s = 0;
        for(int i = 1; i <= n; ++i) {
            int x, y;
            scanf("%d%d", &x, &y);
            p[i] = p[i - 1] + Point(x, y);
            on += gcd(abs(x), abs(y));
            s += (p[i - 1]).cross(p[i]);
        }
        s *= 0.5;
        int in = (int)s - on / 2 + 1;
        printf("Scenario #%d:\n", _);
        printf("%d %d %.1lf\n\n", in, on, s);
    }
    return 0;
}