吴恩达《Machine Learning Yearning》总结（21-30章）

21.偏差和方差举例

前提：对于人类而言，可以达到近乎完美的表现（即人类去做分类是误差可以接近0）。

（1）假设算法的表现如下：训练误差率：1%，开发误差率：11%；此时即为高方差（high variance），也被称为过拟合（overfitting）。

（2）假设算法的表现如下：训练误差：15&，开发误差率：16%；此时即为高偏差（high bias），也被称为欠拟合（underfitting）。

（3）假设算法的表现如下：训练误差：15%，开发误差率：30%；此时即为高偏差和高方差。

（4）假设算法的表现如下：训练误差：0.5%，开发误差率：1%；此时算法已经非常完美。

22.与最优误差率比较

举例：当一个连人类都很难完成（如很多噪音的语音识别）的分类任务，人类的误差率达到14%，此时最完美的误差为14%，该误差称为最优误差率，也称为贝叶斯错误率（Bayes error rate）。以上的最优错误率是可以确定的，但是有些问题如电影推荐，很难去确定其最优误差率是多少。

此时偏差和进一步细化：偏差=最优误差率+可避免偏差；其中可避免偏差高时才值得去优化。

23..处理偏差和方差

（1）如果具有较高的可避免偏差，那么可以加大模型的规模（例如增加神经元的层数、每层神经元的个数）。

（2）如果具有较高的方差，那么可以向训练集增加数据。

其他（3）改变网络的架构，这样会带来新的结果。

在增大网络模型时，会带来高方差的风险，但只要通过适当的正则化（如L2）,或者dropout等策略，就不会出现这样的问题。

24.偏差和方差间的均衡

在现如今，往往可以获得足够的数据，并且足够的算力来支撑非常大的网络，所以不会出现此消彼长的情况。

25.减少可避免偏差的技术

（1）加大模型规模（例如层数/神经元个数），此时加入正则化可以抵消方差的增加。

（2）根据误差分析结果修改输入特征。

（3）减少或者去除正则化。这种方式会增加方差。

（4）修改模型架构。这项技术会同时影响方差和偏差。

26.训练集误差分析

在训练集上也做类似于开发集上的误差分析。

27.减少方差的技术

（1）添加更多的训练数据。

（2）加入正则化（L1,L2,Dropout）,该项会增大偏差。

（3）加入提前终止（比如根据开发集提前终止梯度下降），这项技术会增加偏差，一些学者将其归入正则化技术之一。

（4）通过特征选择减少特征的数量和种类，当数据集很小时，特征选择非常有用。

（5）减小模型规模，谨慎使用。

以下两种方式和减少偏差的策略相同

（6）根据误差分析结果修改输入特征。

（7）修改模型架构。

28.诊断偏差与方差：学习曲线

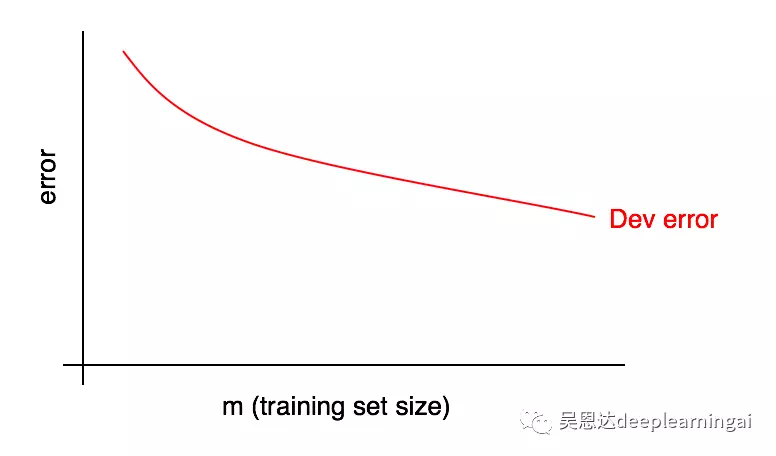
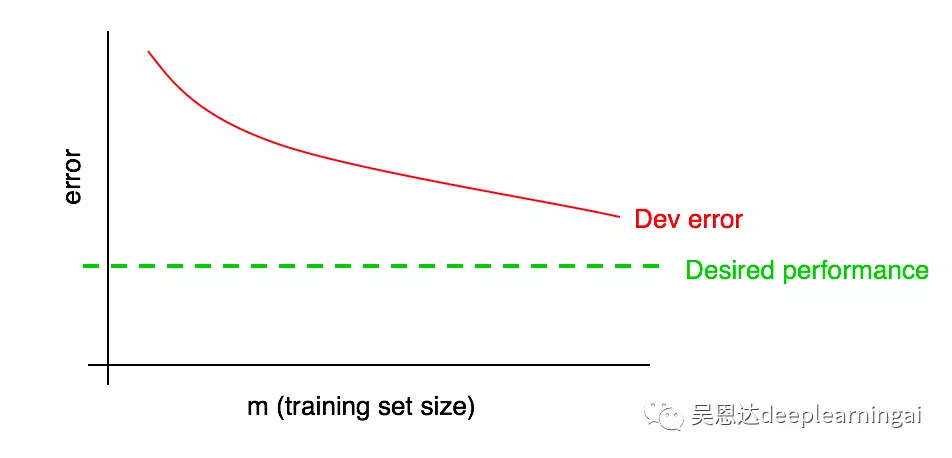
学习1曲线：误差随数据量增加的变化趋势。

学习曲线有一个缺点：当数据量变得越来越多是，将很难预测后续红色曲线的走向。

29.绘制训练误差曲线

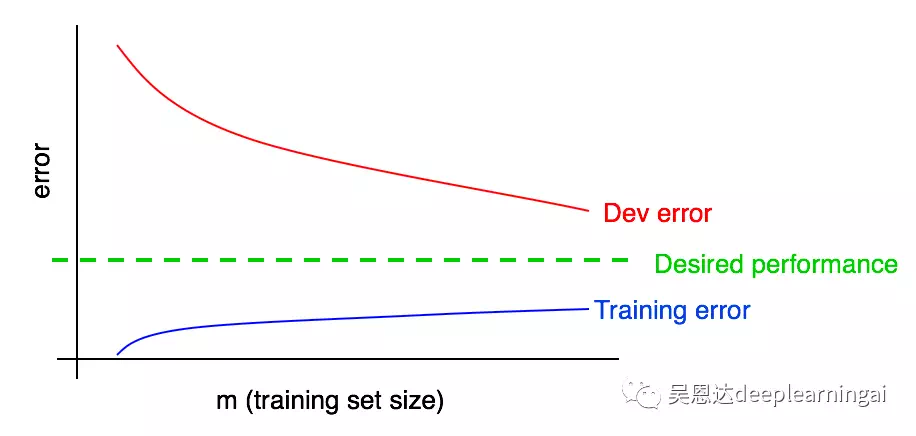
训练误差上升说明：比如两张图片算法很容易就分辨出来，其误差为0，当增加到100张时，就不一定都能正确识别了。

30.解读学习曲线：高偏差

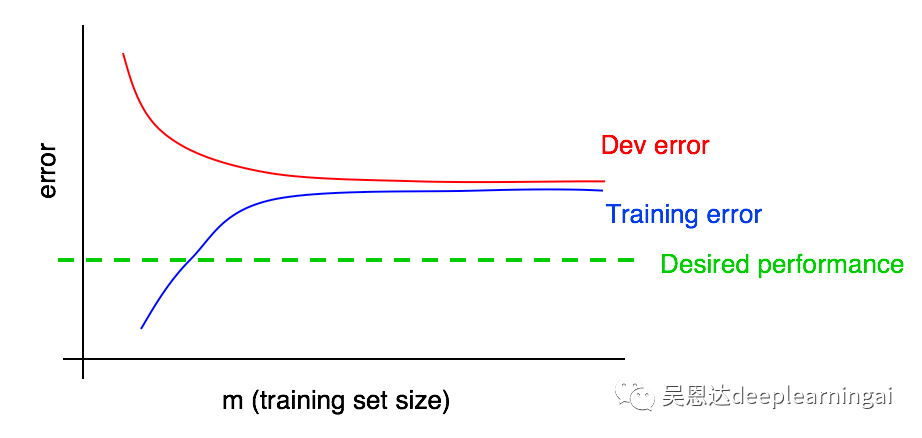
观察结果：

（1）随着我们添加更多的训练数据，训练误差只会变得更糟，因此蓝色的训练误差曲线只会保持不动或上升，这表明它只会远离期望的性能水平（绿色的线）。

（2）红色的开发误差曲线通常要高于蓝色的误差曲线，因此只要训练误差高于期望性能水平，通过添加更多数据来让红色开发误差曲线下降到期望性能水平之下也基本不可能。

之前我们讨论的都是曲线的最右端，而通过学习曲线则更加的群面了解算法。