（五）用正则化(Regularization)来解决过拟合

1 过拟合

过拟合就是训练模型的过程中，模型过度拟合训练数据，而不能很好的泛化到测试数据集上。出现over-fitting的原因是多方面的：

1） 训练数据过少，数据量与数据噪声是成反比的，少量数据导致噪声很大

2 ）特征数目过多导致模型过于复杂，如下面的图所示：

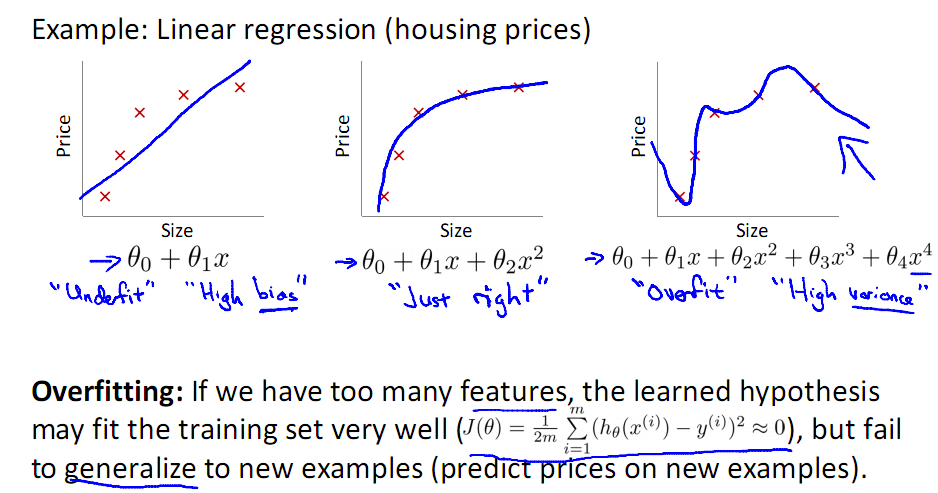
看上图中的多项式回归（Polynomial regression），左边为模型复杂度很低，右边的模型复杂度就过高，而中间的模型为比较合适的模型，对于Logistic有同样的情况

2）如何避免过拟合

1） 控制特征的数目，可以通过特征组合，或者模型选择算法

2）Regularization，保持所有特征，但是减小每个特征的参数向量θ的大小，使其对分类y所做的共享很小

下面来详细分析正则化

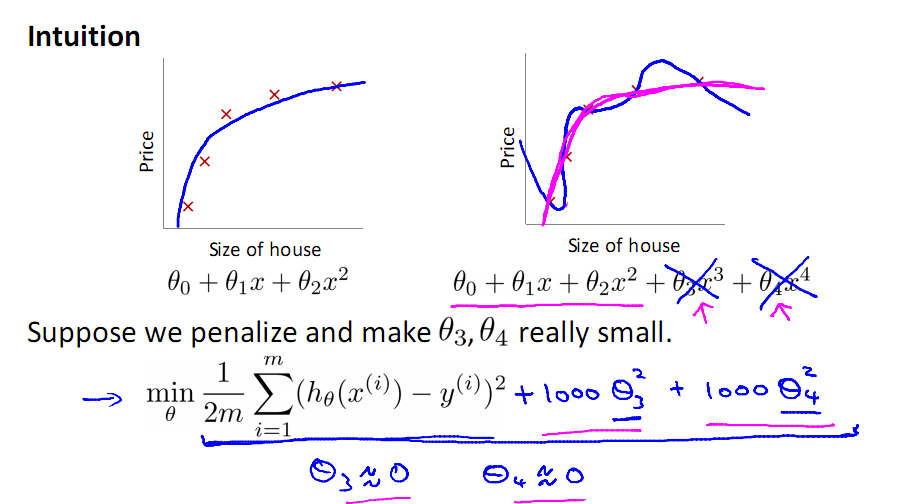
来看多项式拟合的问题，对于右图复杂的模型，只需控制θ₃与θ₄的大小，即可使得模型达到与作图类似的结果，下面引入线性回归的L2正则的公式

如上过程就是正则化的过程，注意正则化是不带θ₀的，其实带不带在实际运用中只会有很小的差异，所以不必在意，现在只需要控制λ的大小，当λ很大时，θ₁到θ_n就会很小，即达到了约束数量庞大的特征的目的。

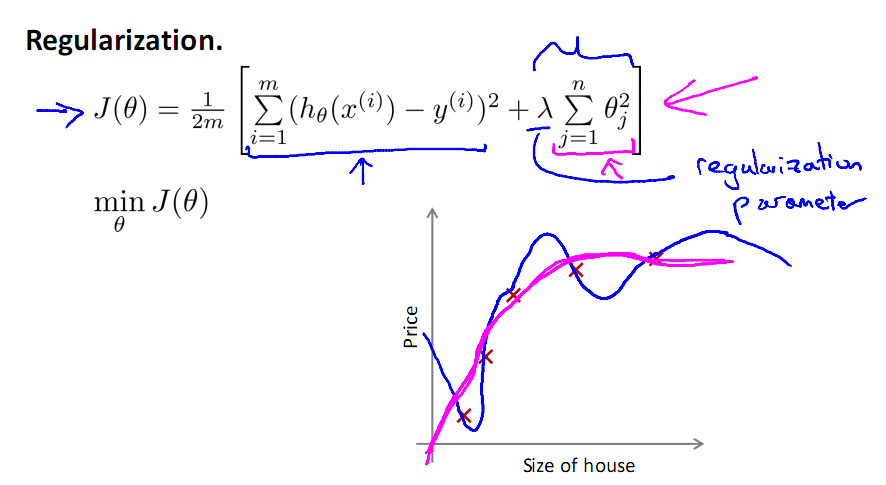
若选择过大的λ，会使得参数向量θ非常小，从而只剩下θ₀，使得模型看起来像一条直线

而且，模型会欠拟合，梯度下降也不会收敛，而λ的选择将在特征选择中讲到

带有正则化项的梯度下降算法，首先要特殊处理θ_0,

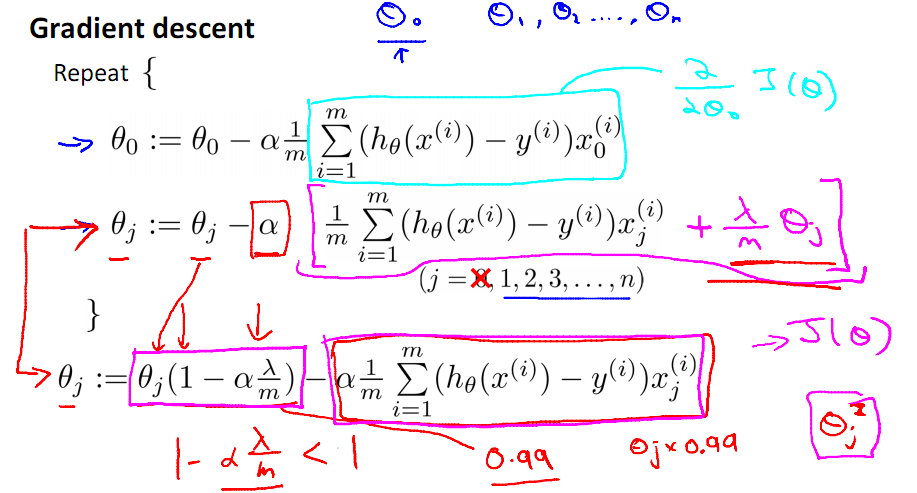
关于Normal Equation 的正则化

并且有一个不错的消息就是括号中的矩阵必定为可逆的

Logistic的正则化

首先看L2正则

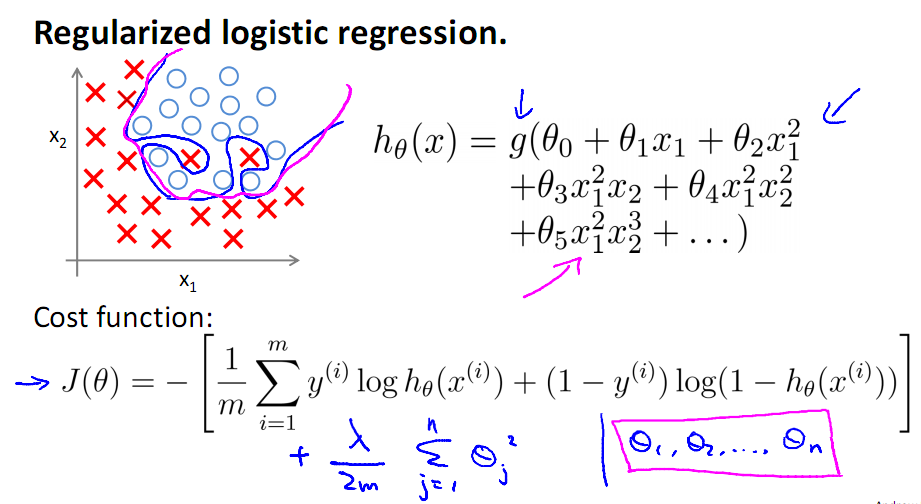
其正则化的Gradient Descent形式：

 3 正则化的一些概念

1）概念

　　L0正则化的值是模型参数中非零参数的个数。

　　L1正则化表示各个参数绝对值之和。

　　L2正则化标识各个参数的平方的和的开方值。

2）正则化后会导致参数稀疏，一个好处是可以简化模型，避免过拟合。因为一个模型中真正重要的参数可能并不多，如果考虑所有的参数起作用，那么可以对训练数据可以预测的很好，但是对测试数据就只能呵呵了。另一个好处是参数变少可以使整个模型获得更好的可解释性。

且参数越小，模型就会越简单，这是因为越复杂的模型，越是会尝试对所有的样本进行拟合，甚至包括一些异常样本点，这就容易造成在较小的区间里预测值产生较大的波动，这种较大的波动也反映了在这个区间里的导数很大，而只有较大的参数值才能产生较大的导数。因此复杂的模型，其参数值会比较大。

3）三种正则概述

-》L0正则化

根据上面的讨论，稀疏的参数可以防止过拟合，因此用L0范数（非零参数的个数）来做正则化项是可以防止过拟合的。

从直观上看，利用非零参数的个数，可以很好的来选择特征，实现特征稀疏的效果，具体操作时选择参数非零的特征即可。但因为L0正则化很难求解，是个NP难问题，因此一般采用L1正则化。L1正则化是L0正则化的最优凸近似，比L0容易求解，并且也可以实现稀疏的效果。

-》L1正则化

L1正则化在实际中往往替代L0正则化，来防止过拟合。在江湖中也人称Lasso。

L1正则化之所以可以防止过拟合，是因为L1范数就是各个参数的绝对值相加得到的，我们前面讨论了，参数值大小和模型复杂度是成正比的。因此复杂的模型，其L1范数就大，最终导致损失函数就大，说明这个模型就不够好。

-》L2正则化

L2正则化可以防止过拟合的原因和L1正则化一样，只是形式不太一样。

L2范数是各参数的平方和再求平方根，我们让L2范数的正则项最小，可以使W的每个元素都很小，都接近于0。但与L1范数不一样的是，它不会是每个元素为0，而只是接近于0。越小的参数说明模型越简单，越简单的模型越不容易产生过拟合现象。

L2正则化江湖人称Ridge，也称“岭回归”

4）几何解释

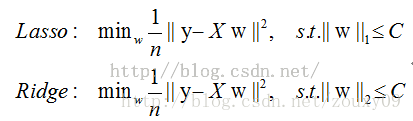
我们考虑两维的情况，在(w1, w2)平面上可以画出目标函数的等高线，而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解：

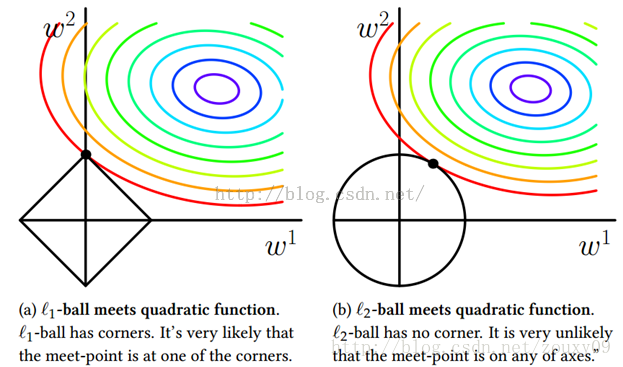
可以看到，L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现，有很大的几率等高线会和L1-ball在四个角，也就是坐标轴上相遇，坐标轴上就可以产生稀疏，因为某一维可以表示为0。而等高线与L2-ball在坐标轴上相遇的概率就比较小了。

总结：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。在所有特征中只有少数特征起重要作用的情况下，选择Lasso比较合适，因为它能自动选择特征。而如果所有特征中，大部分特征都能起作用，而且起的作用很平均，那么使用Ridge也许更合适。

参考：1） NG讲义

　　　2） http://blog.csdn.net/zouxy09/article/details/24971995/