iOS线程 - GCD在开发中的常见问题

GCD 在开发中的常见问题

1 - 主线程中调用方法

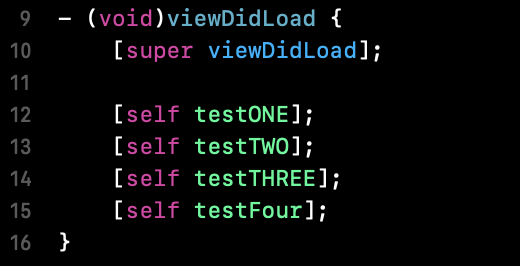
① 执行 testONE 后的输出结果：1  5  2  4  3

 1 -(void)testONE{
 2
 3     // 并发队列
 4     dispatch_queue_t queue = dispatch_queue_create("cooci",DISPATCH_QUEUE_CONCURRENT);
 5     NSLog(@"1");
 6
 7     // 异步函数
 8     dispatch_async(queue, ^{
 9         NSLog(@"2");
10
11         // 异步函数
12         dispatch_async(queue, ^{
13             NSLog(@"3");
14         });
15
16         NSLog(@"4");
17     });
18
19     NSLog(@"5");
20
21 }

② 执行 testTWO 后理论上输出结果：1  5  2  3  4，实际是 crash

 1 // crash
 2 -(void)testTWO{
 3
 4     // 串行队列
 5     dispatch_queue_t queue = dispatch_queue_create("cooci",DISPATCH_QUEUE_SERIAL);
 6     NSLog(@"1");
 7
 8     // 异步函数
 9     dispatch_async(queue, ^{
10         NSLog(@"2");
11
12         // 任务 3 会阻塞线程，任务 4 需要等待 任务 3 执行完毕后方可执行
13         // 但是由于是异步函数，任务 4 根本不需要等待 任务 3 的执行
14         // 那么就会造成死锁问题，程序崩溃
15         dispatch_sync(queue, ^{
16             NSLog(@"3");
17         });
18
19         NSLog(@"4");
20     });
21
22     NSLog(@"5");
23
24 }

③ 执行 testTHREE 后输出结果：任务 1、2、3 首先无序执行；其次执行 任务 0（必定排在第四位）；任务 4、5、6 最后无序执行

 1 -(void)testTHREE{
 2
 3     // 并发队列
 4     dispatch_queue_t queue = dispatch_queue_create("cooci",DISPATCH_QUEUE_CONCURRENT);
 5
 6     // 异步
 7     dispatch_async(queue, ^{
 8         NSLog(@"1");
 9     });
10     // 异步
11     dispatch_async(queue, ^{
12         NSLog(@"2");
13     });
14     // 同步
15     dispatch_sync(queue, ^{
16         NSLog(@"3");
17     });
18
19     // 主线程
20     // ------------------
21     NSLog(@"0");
22     // ------------------
23
24
25     // 异步
26     dispatch_async(queue, ^{
27         NSLog(@"4");
28     });
29     // 异步
30     dispatch_async(queue, ^{
31         NSLog(@"5");
32     });
33     // 同步
34     dispatch_sync(queue, ^{
35         NSLog(@"6");
36     });
37
38 }

④ 多线程是不安全的，使用不规范极易出现抢占公共资源的问题

 1 // 线程锁即可解决该问题
 2 -(void)testFour{
 3
 4     __block int a = 0;
 5     while (a < 4) {
 6
 7         // 抢占资源问题：多线程是不安全的
 8         // 因为异步执行，则极有可能有一瞬间（一瞬间在计算机内部可以干 N 多事！我们想象有一台计算机极其强悍）存在多个异步函数同时在处理 a++
 9         dispatch_async(dispatch_get_global_queue(0, 0), ^{
10             a++;
11         });
12     }
13     // 输出结果必定 >= 4
14     NSLog(@"%d",a);
15 }