拉格朗日插值法--python

数据插补

常见插补方法

插值法--拉格朗日插值法

根据数学知识可知，对于平面上已知的n个点（无两点在一条直线上可以找到n-1次多项式



,使次多项式曲线过这n个点。

1）求已知过n个点的n-1次多项式：

将n个点的坐标带入多项式：得到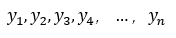

解出拉格朗日插值多项式：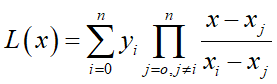

将缺失的函数值对应的点x带入多项式得到趋势值得近似值L(x)

实验数据来源

链接：https://pan.baidu.com/s/1jiIOoselsqVQR4P_EaS3pA

提取码：t970

代码

#拉格朗日插值代码
import pandas as pd #导入数据分析库Pandas
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import lagrange #导入拉格朗日插值函数

inputfile = '../data/data.xlsx' #销量数据路径
outputfile = '../tmp/sales.xls' #输出数据路径

data = pd.read_excel(inputfile) #读入数据
temp = data[u'销量'][(data[u'销量'] < 400) | (data[u'销量'] > 5000)] #找到不符合要求得值 data[列][行]
for i in range(temp.shape[0]):
    data.loc[temp.index[i],u'销量'] = np.nan #把不符合要求得值变为空值

#自定义列向量插值函数
#s为列向量，n为被插值的位置，k为取前后的数据个数，默认为5
def ployinterp_column(s, n, k=5):
  y = s.iloc[list(range(n-k, n)) + list(range(n+1, n+1+k))] #取数 就是传入得data
  y = y[y.notnull()] #剔除空值
  f = lagrange(y.index, list(y))
  return f(n) #插值并返回插值结果

#逐个元素判断是否需要插值
for i in data.columns:
  for j in range(len(data)):
    if (data[i].isnull())[j]: #如果为空即插值。
        data.loc[j,i] = ployinterp_column(data[i], j)

data.to_excel(outputfile) #输出结果，写入文件
print("success")

运行结果：

这个代码是可以运行的

---

问题

没有报SettingWithCopyWarning: A value is trying to be set on a copy of a slice from a DataFrame



我也不知道时怎么把这个警告消除的，反正就是找啊找，在我不注意的时候能运行了！好像是不能一下多个赋值，要分开赋值。

最后

但是我们细看可以发现插入的值有问题：把插入的值输出可以看到有一个异常值

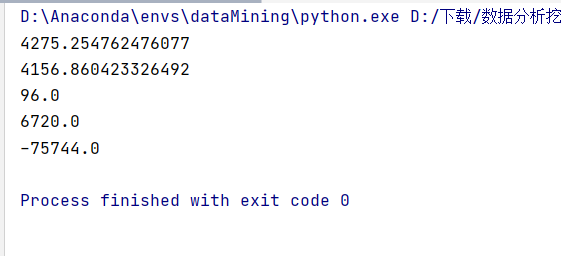
我们在处理数据时把小于400，大于5000的值都变成空值，然后通过拉格朗日插值法插入值，想要把数据没有那么大的差值，但是给我们插入一个负数，并且很离谱。我检查了一下并没有发现哪里有错误；然后我把用到的数据和拟合出来的拉格朗日函数输出得到：

f=-0.008874 x + 11.53 x - 6657 x + 2.242e+06 x - 4.854e+08 x + 7.005e+10 x - 6.74e+12 x + 4.168e+14 x - 1.504e+16 x + 2.411e+17



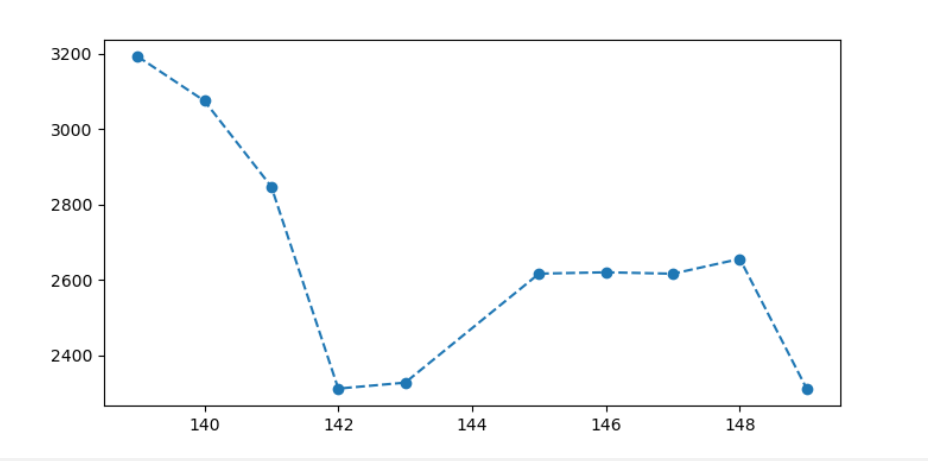
并没有发现问题，让后我就想着是不是拟合出来的函数步够精确，我把取点增加，但是都没有好的结果，反而更离谱，这种情况就是过拟合了，就是这个模型可以把你训练的模型拟合的很好，但是测试模型并不好。

举个例子：下面一组数据可以看到用x^{4函数拟合的并没有太多的点在模型上，x}4函数拟合的相对较多一点，但是如果进行测试，14次方的模型可能会预测的很离谱：

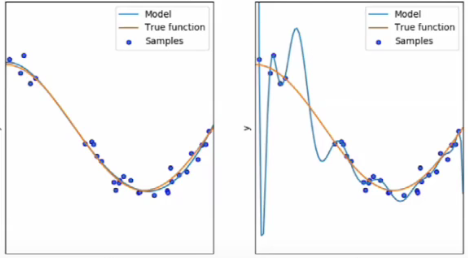
最后我把取值点减小发现上下取点4个时都会有一个好的结果，上下去点为3，2，1（直线，不建议取）时也都还能接受。所以我么拟合出来的五个上下点时也并没有错，只是它拟合出来的函数就是在那个点上数值离谱。