快速用梯度下降法实现一个Logistic Regression 分类器

前阵子听说一个面试题：你实现一个logistic Regression需要多少分钟？搞数据挖掘的人都会觉得实现这个简单的分类器分分钟就搞定了吧？

因为我做数据挖掘的时候，从来都是顺手用用工具的，尤其是微软内部的TLC相当强大，各种机器学习的算法都有，于是自从离开学校后就没有自己实现过这些基础的算法。当有一天心血来潮自己实现一个logistic regression的时候，我会说用了3个小时么？。。。羞羞

---------------------------------------------------前言结束----------------------------------------------

当然logistic regression的渊源还是有点深的，想复习理论知识的话可以去http://en.wikipedia.org/wiki/Logistic_regression ， 我这里就直接讲实现啦。

首先要了解一个logistic function

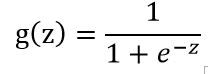
这个函数的图像是这个样子的：

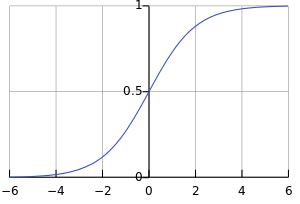
而我们要实现的logistic regression model，就是要去学习出一组权值w：

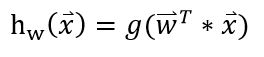
x 指feature构成的向量。 这个向量w就可以将每个instance映射到一个实数了。

假如我们要出里的是2分类问题，那么问题就被描述为学习出一组w，使得h(正样本)趋近于1， h(负样本)趋近于0.

现在就变成了一个最优化问题，我们要让误差最小化。 现在问题来了，怎么定义误差函数呢？

首先想到的是L2型损失函数啦，于是啪啪啪写上了

。

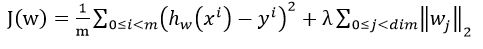很久没有复习logistic regression的人最容易犯错的就是在这了。正确的写法是：

，

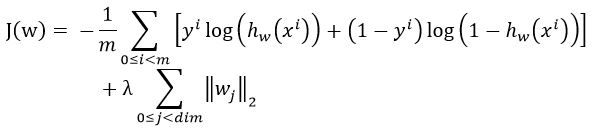然后对它求偏导数得到梯度下降法的迭代更新方程：

。

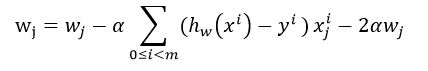于是你会发现这个迭代方程是和线性回归的是一样的！

理清了过程时候，代码就变得异常简单了：

  public class LogisticRegression
     {
         private int _maxIteration = ;
         private double _stepSize = 0.000005;
         //private double _stepSize = 0.1;
         private double _lambda = 0.1;
         private double decay = 0.95;

         public int dim;
         public double[] theta;

         public LogisticRegression(int dim)
         {
             this.dim = dim;
         }

         public LogisticRegression(int dim, double stepSize)
             : this(dim)
         {
             this._stepSize = stepSize;
         }

         public void Train(Instance[] instances)
         {
             Initialize();

             int instCnt = instances.Length;
             double[] dev =new double[this.dim];
             for (int t = ; t < this._maxIteration; t++)
             {
                 double cost = ;
                 for (int i = ; i < instCnt; i++)
                 {
                     double h_x = MathLib.Logistic(MathLib.VectorInnerProd(instances[i].featureValues, this.theta));
                     // calculate cost function
                     cost += instances[i].label * Math.Log(h_x) + ( - instances[i].label) * Math.Log( - h_x);
                 }
                 cost *= -1.0 / instCnt;
                 Console.WriteLine("{0},{1}", t, cost);

                 for (int i = ; i < instCnt; i++)
                 {
                     ResetArray(dev);
                     double h_x = MathLib.Logistic(MathLib.VectorInnerProd(instances[i].featureValues, this.theta));
                     double error =   h_x- instances[i].label ;
                     for (int j = ; j < this.dim; j++)
                     {
                         dev[j] += error*instances[i].featureValues[j] + *dev[j]*this._lambda;
                         this.theta[j] -= this._stepSize * dev[j] ;
                         //BoundaryLimiting(ref this.theta[j], 0, 1);
                     }
                 }
                 //this._stepSize *= decay;
                 //if (this._stepSize > 0.000001)
                 //{
                 //    this._stepSize = 0.000001;
                 //}
             }
         }

         private void BoundaryLimiting(ref double alpha, double lowerbound, double upperbound)
         {
             if (alpha < lowerbound)
             {
                 alpha = lowerbound;
             }
             else if (alpha > upperbound)
             {
                 alpha = upperbound;
             }
         }

         public double[] Predict(Instance[] instances)
         {
             double[] results = new double[instances.Length];
             for (int i = ; i < results.Length; i++)
             {
                 results[i] = MathLib.Logistic(MathLib.VectorInnerProd(instances[i].featureValues, this.theta));
             }
             return results;
         }

         private void ResetArray(double[] dev)
         {
             for (int i = ; i < dev.Length; i++)
             {
                 dev[i] = ;
             }
         }

         private void Initialize()
         {
             Random ran = new Random(DateTime.Now.Second);

             this.theta = new double[this.dim];
             for (int i = ; i < this.dim; i++)
             {
                 this.theta[i] = ran.NextDouble() *  ; // initialize theta with a small value
             }
         }

         public static void Test()
         {
             LogisticRegression lr = new LogisticRegression();

             List<Instance> instances = new List<Instance>();
             using (StreamReader rd = new StreamReader(@"D:\\local exp\\data.csv"))
             {
                 string content = rd.ReadLine();
                 while ((content = rd.ReadLine()) != null)
                 {
                     instances.Add(Instance.ParseInstance(content,','));
                 }
             }

            // MinMaxNormalize(instances); 

             lr.Train(instances.ToArray()); 

         }

         private static void MinMaxNormalize(List<Instance> instances)
         {
             int dim = instances[].dim;
             double[] min = new double[dim];
             double[] max = new double[dim];

             int instCnt = instances.Count;
             for (int i = ; i < instCnt; i++)
             {
                 for (int j = ; j < dim; j++)
                 {
                     if (i ==  || instances[i].featureValues[j] < min[j])
                     {
                         min[j] = instances[i].featureValues[j];
                     }
                     if (i ==  || instances[i].featureValues[j] > max[j])
                     {
                         max[j] = instances[i].featureValues[j];
                     }
                 }
             }

             for (int j = ; j < dim; j++)
             {
                 double gap = max[j] - min[j];
                 if (gap <= )
                 {
                     continue;
                 }
                 for (int i = ; i < instCnt; i++)
                 {
                     instances[i].featureValues[j] = (instances[i].featureValues[j] - min[j]) / gap;
                 }
             }

         }
     }

前面提到说我花了3个小时，其中很大一部分原因是在debug算法为啥没有收敛。这里有个很重要的步骤是把feature规范化到[0,1] 。 如果不normalize的话，参数调起来比较麻烦，loss function也经常蹦到NaN去了。

以下是对比normalize和不加normalization的收敛曲线图：

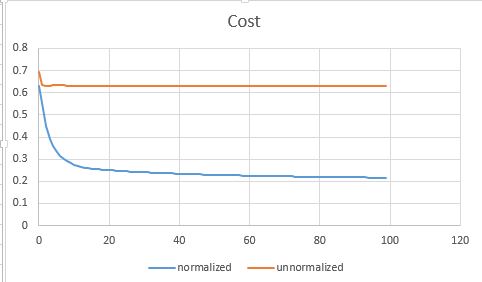
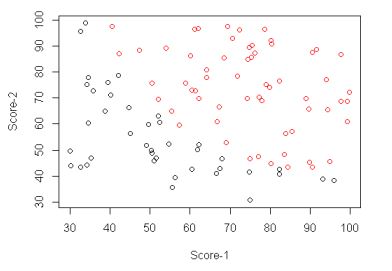
我用的实现数据可以在 http://pingax.com/wp-content/uploads/2013/12/data.csv  下载到。 它是一个2维的数据， 分布如下：