HDU 1054 Strategic Game（树形DP）

Strategic Game

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2925    Accepted Submission(s): 1222

Problem Description

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

The input file contains several data sets in text format. Each data set represents a tree with the following description:

the number of nodes
the description of each node in the following format
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifier
or
node_identifier:(0)

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500). Every edge appears only once in the input data.

For example for the tree:

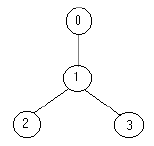
the solution is one soldier ( at the node 1).

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following table:

 

Sample Input

4

0:(1) 1

1:(2) 2 3

2:(0)

3:(0)

5

3:(3) 1 4 2

1:(1) 0

2:(0)

0:(0)

4:(0)

 

Sample Output

1

2

#include <iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
struct node
{
    int brother,child;
    int yes；//该点放士兵
    int no;  //该点不放士兵
}tree[];
int n,i,j,k,root,num,origin;

void dfs(int root)
{
   int  child=tree[root].child;
  while(child>)
   {
       dfs(child);
       tree[root].yes+=min(tree[child].yes,tree[child].no);
        //父亲结点放置了，儿子结点可以放置也可以不放置
       tree[root].no+=tree[child].yes;
        //父亲结点没有放置，儿子结点必须放置
       child=tree[child].brother;
   }
}
int main()
{
    while(~scanf("%d",&n))
    {
      for(i=;i<=n;i++)
      {
            tree[i].brother=tree[i].child=;
            tree[i].yes=;
            tree[i].no=;
      }
      for(int t=;t<=n;t++)
      {
        scanf("%d:(%d)",&root,&num);
        root++;
         if (t==) origin=root;
        for(i=;i<=num;i++)
        {
            int x;
            scanf("%d",&x);
            x++;
            tree[x].brother=tree[root].child;
            tree[root].child=x;
        }
      }
      dfs(origin);
      printf("%d\n",min(tree[origin].yes,tree[origin].no));
    }

    return ;
}

代码二：

dproot[ i ]表示以i为根的子树，在i上放置一个士兵，看守住整个子树需要多少士兵。

all[ i ]表示看守住整个以i为根的子树需要多少士兵。

状态转移方程：

叶子节点： dproot[k] =1； all[k] = 0；

非叶子节点： dproot[i] = 1 + ∑all[j](j是i的儿子)；

　　　　　　all[i] = min( dproot[i], ∑dproot[j](j是i的儿子) );

#include <iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int M=+;
int dproot[M],all[M];
int i,n,x,y,k;
vector<int> v[M];
void dfs(int x,int fa)
{
    int tmp=;
    for(int i=;i<v[x].size();i++)
    {
        int k=v[x][i];
        if (k==fa) continue;
        dfs(k,x);
        dproot[x]+=all[k];
        tmp=tmp+dproot[k];
    }
    all[x]=min(dproot[x],tmp);
return;
}
int main()
{
    while(~scanf("%d",&n))
    {
        for(i=;i<n;i++)
            {
                v[i].clear();
                all[i]=;
                dproot[i]=;
            }
        for(int t=;t<=n;t++)
        {
            scanf("%d:(%d)",&x,&y);
            for(i=;i<=y;i++)
            {
                scanf("%d",&k);
                v[x].push_back(k);
                v[k].push_back(x);
            }
        }
       dfs(,-);
       printf("%d\n",all[]);
    }
    return ;
}

　　

Source

Southeastern Europe 2000