SGI STL泛型heap算法分析

heap性质

heap本质是用一个数组表示的完全二叉树，并且父节点总是大于（或者小于）子节点的值。在STL中用于实现优先队列（priority_queque）。堆排序是排序算法中是稳定效率最高的一种。STL以可以动态扩容的vector作为heap的底层数组。

push_heap分析

为满足完全二叉树的条件，新加入元素一定要放在最下一层作为叶子节点，并填补由左至右的第一个空格，也就是把新元素插入到底层vector的end()处。下图是push_heap算法的实际示意图：

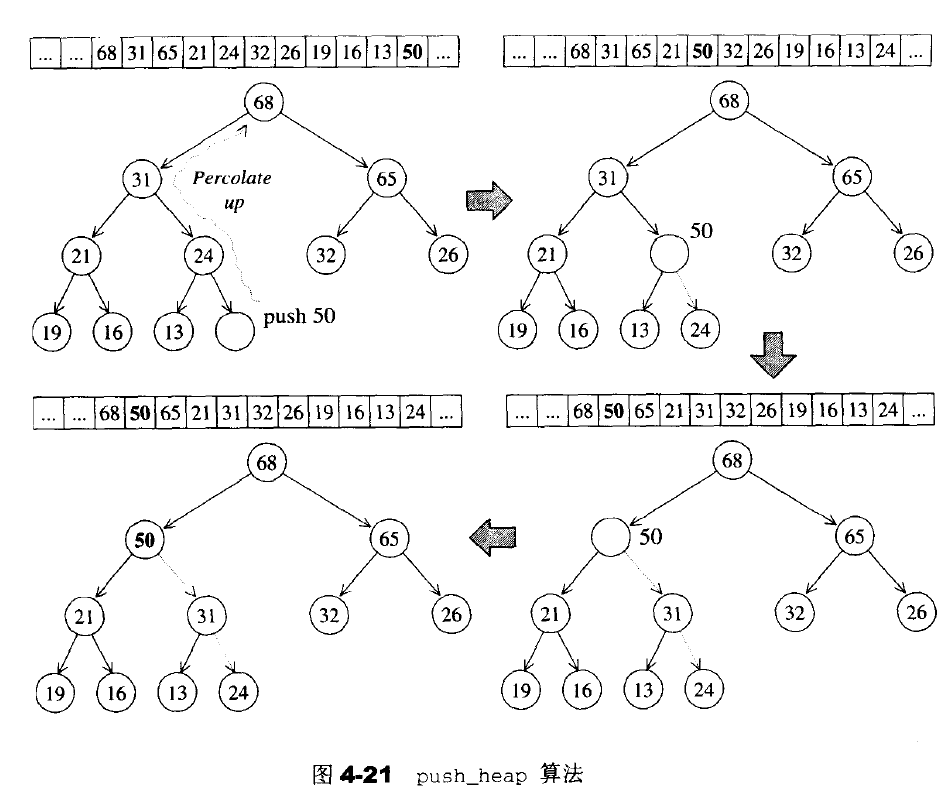
从图中可以看出push_heap算法的过程是将新加入堆的值（50），层层上挪，直到正确的位置。下面是该过程的源码：

template <class RandomAccessIterator, class Distance, class T>
void __push_heap(RandomAccessIterator first, Distance holeIndex,
                 Distance topIndex, T value) {
  Distance parent = (holeIndex - ) / ;  //找出父节点
  while (holeIndex > topIndex && *(first + parent) < value) {
    //尚未到达顶端且父节点小于洞值，使用operator<，知max-heap
    *(first + holeIndex) = *(first + parent);  //令洞值为父值
    holeIndex = parent;                        //新洞为父节点
    parent = (holeIndex - ) / ;              //新洞的父节点
  }
  *(first + holeIndex) = value;  //令洞值为新值
}

template <class RandomAccessIterator, class Distance, class T>
inline void __push_heap_aux(RandomAccessIterator first,
                            RandomAccessIterator last, Distance*, T*) {
  __push_heap(first, Distance((last - first) - ), Distance(),
              T(*(last - )));
  //(last-first)–1代表新元素的索引，0是堆首的索引，*(last - 1)是新加入的值
}

template <class RandomAccessIterator>
inline void push_heap(RandomAccessIterator first, RandomAccessIterator last) {
  //注意，调用该函数时候，新元素位于最后一个位置(last-1)
  __push_heap_aux(first, last, distance_type(first), value_type(first));
}

push_heap的用法是输入迭代器对，并且保证[first,last-1)是最大堆，*(last-1)是新加入的元素。push_heap调用辅助函数__push_heap_aux。至于为什么需要这个辅助函数了？应该是为了提取出distance_type和value_type吧，这两个内联函数的定义，可以参考stl源码剖析迭代器的那章。下面来思考真正的实现函数__push_heap。这个函数需要新加入元素位置holeIndex和堆首位置topIndex，另外还有保存好的新加入值。算法的过程很简单，就是上溯holeIndex，找到真正满足条件的位置（无法继续上回溯），然后把value放入该位置即可。

pop_heap分析

pop_heap操作取走根节点，其实是移至底部容器vector的最后一个节点处并保存该节点。而此时需要维护vector.size()-1大小堆，需要为保存的节点在堆中找一个适当的位置。这个过程和上面的__push_heap的过程恰好相反，从根节点（此时为洞节点），层层下放，直到叶子节点位置，然后在这个位置调用push_heap加入刚刚保存的新值。下面是pop_heap算法实际示意图：

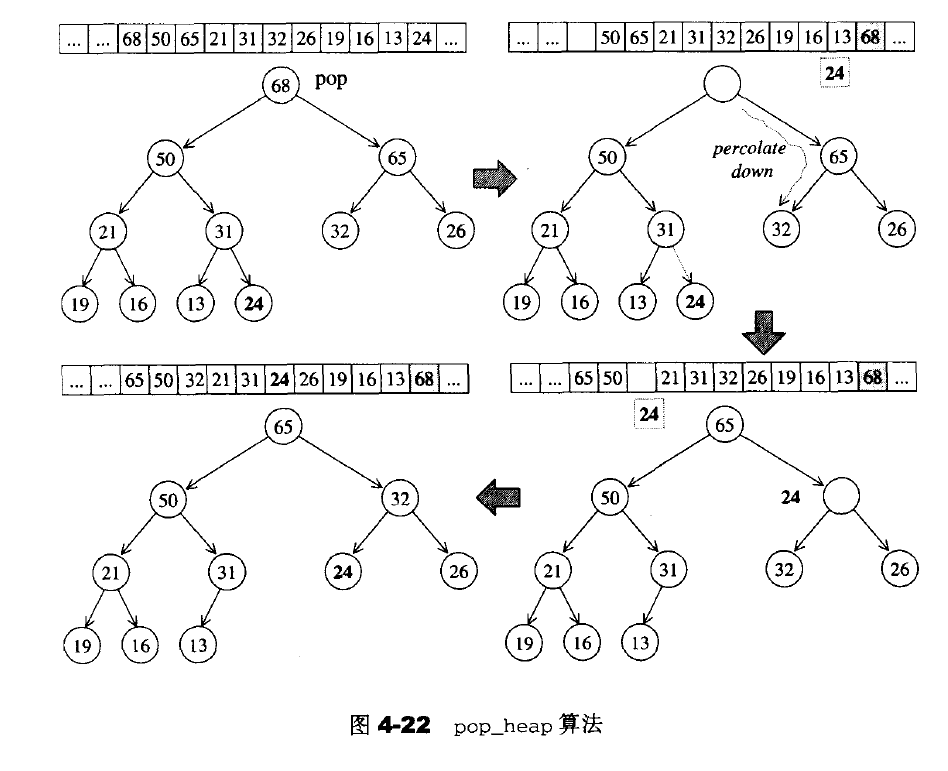
下面看pop_heap的源码：

template <class RandomAccessIterator, class Distance, class T>
void __adjust_heap(RandomAccessIterator first, Distance holeIndex,
                   Distance len, T value) {
  Distance topIndex = holeIndex;
  Distance secondChild =  * holeIndex + ;  //洞节点的右子节点
  while (secondChild < len) {
    if (*(first + secondChild) < *(first + (secondChild - )))  //左节点值大于右节点值
      secondChild--;  //洞节点往左下放
    *(first + holeIndex) = *(first + secondChild);  //洞节点下放
    holeIndex = secondChild;  //新洞节点
    secondChild =  * (secondChild + );  //新洞节点的右子节点
  }
  if (secondChild == len) {  //如果只有左子节点，洞节点下放到左子节点
    *(first + holeIndex) = *(first + (secondChild - ));
    holeIndex = secondChild - ;
  }
  __push_heap(first, holeIndex, topIndex, value);  //原尾值插入到新数组中，上溯
}

template <class RandomAccessIterator, class T, class Distance>
inline void __pop_heap(RandomAccessIterator first, RandomAccessIterator last,
                       RandomAccessIterator result, T value, Distance*) {
  *result = *first;  //设定尾值为首值，于是尾值即是结果，
    //可由调用底层容器之 pop_back() 取出尾值
  __adjust_heap(first, Distance(), Distance(last - first), value);
  //以上欲重新调整 heap，洞号为 0，欲调整值为value
}

template <class RandomAccessIterator, class T>
inline void __pop_heap_aux(RandomAccessIterator first,
                           RandomAccessIterator last, T*) {
  __pop_heap(first, last - , last - , T(*(last - )), distance_type(first));
  //pop动作的结果为底层容器的第一个元素。因此，首先设定欲调整值为尾值，然后將首值调至
    //尾节点（所以以上将迭代器result设为last-1）。然后重整 [first, last-1)，
    //使之重新成一个合格的 heap
}

template <class RandomAccessIterator>
inline void pop_heap(RandomAccessIterator first, RandomAccessIterator last) {
  __pop_heap_aux(first, last, value_type(first));
}

类似于push_heap，pop_heap也是调用辅助函数__pop_heap_aux。__pop_heap_aux调用__pop_heap。__pop_heap调用__adjust_heap调整holeIndex，最终在holeIndex处调用push_heap函数插入value（原最后一个的值）。关键代码是__adjust_heap中的循环。循环的主要意思是将holeIndex不断下放，直到最底层。最后的if语句的意思是，如果最底层有左子节点，而没有右子节点，那么最终位置肯定是这个左子节点。侯捷注释说，最后一句代码的意思是加入value到holeIndex，由于已经调整完毕，所以一个赋值操作也可以达到要求。这种说法其实是错误的，如果__adjust_heap只是用在pop_heap实现完全没有问题，但在下面的make_heap也用到__adjust_heap这个函数，此时一个赋值操作是完全达不到目的的。因为make_heap调整__adjust_heap调整时value和子树中的节点的值的大小是还不确定的，需要上溯加入。后面有测试验证。

make_heap分析

这个算法用来将一段现有的数据转化为一个heap，即将一个迭代器对的内容构造成最大堆。代码如下：

template <class RandomAccessIterator, class T, class Distance>
void __make_heap(RandomAccessIterator first, RandomAccessIterator last, T*,
                 Distance*) {
  if (last - first < ) return;  //如果长度小于2，不必排序直接退出
  Distance len = last - first;
  //找出第一个需要重排的子树头部，以 parent 标示出。由于任何叶节点都不需执行
    //perlocate down，所以有以下計算
  Distance parent = (len - )/;

  while (true) {
    //调整以 parent 为首的子树。len 是为了 __adjust_heap() 判断做范围
    __adjust_heap(first, parent, len, T(*(first + parent)));
    if (parent == ) return;  //走完根节点结束
    parent--;  //重排子树头部退一格
  }
}

template <class RandomAccessIterator>
inline void make_heap(RandomAccessIterator first, RandomAccessIterator last) {
  __make_heap(first, last, value_type(first), distance_type(first));
}

__make_heap中代码的思路也很简单。从原序列的中间位置开始不断调整（调用__adjust_heap），每次调整的目的是以当前位置为根的构建一个子堆。至于为什么从中间位置开始就可以了？原因很简单，最底层元素的数目大致就会占了一半了。

sort_heap分析

sort_heap就比较简单了，不断将极值移动到末尾，不断pop_heap。代码如下：

//每执行一次 pop_heap()，极值（在STL heap中为极大值）即被放在尾端。
//扣除尾端再执行一次 pop_heap()，次极值又被放在新尾端。一直下去，最后即得排序結果。
//每执行 pop_heap() 一次，操作范围即退缩一格
template <class RandomAccessIterator>
void sort_heap(RandomAccessIterator first, RandomAccessIterator last) {
  while (last - first > ) pop_heap(first, last--);
}

测试验证

测试代码：

void test_heap() {
    int ia[] = {, , , , , , , , };
    STD::vector<int> vec(ia, ia+);
    STD::make_heap(vec.begin(), vec.end());
    for (auto i : vec) {
        std::cout << i << " ";
    }
    std::cout << std::endl;

    std::cout << "sort_heap:" << std::endl;
    STD::sort_heap(vec.begin(), vec.end());
    for (auto i : vec) {
        std::cout << i << " ";
    }
    std::cout << std::endl;
}

结果：

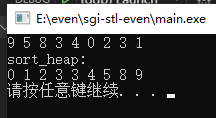
如果按照上文将的在__adjust_heap实现中用一个赋值操作代替push_heap函数，即__adjust_heap实现改为如下：

template <class RandomAccessIterator, class Distance, class T>
void __adjust_heap(RandomAccessIterator first, Distance holeIndex,
                   Distance len, T value) {
  Distance topIndex = holeIndex;
  Distance secondChild =  * holeIndex + ;  //洞节点的右子节点
  while (secondChild < len) {
    if (*(first + secondChild) < *(first + (secondChild - )))  //左节点值大于右节点值
      secondChild--;  //洞节点往左下放
    *(first + holeIndex) = *(first + secondChild);  //洞节点下放
    holeIndex = secondChild;  //新洞节点
    secondChild =  * (secondChild + );  //新洞节点的右子节点
  }
  if (secondChild == len) {  //如果只有左子节点，洞节点下放到左子节点
    *(first + holeIndex) = *(first + (secondChild - ));
    holeIndex = secondChild - ;
  }
  *(first + holeIndex) = value;
  // __push_heap(first, holeIndex, topIndex, value);  //原尾值插入到新数组中，上溯
}

继续运行上面一开始的测试代码，结果：

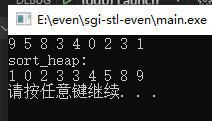
所以，侯捷的说法是错误的，遵循源码的实现才正确。