BZOJ 1833 数字计数 数位DP

题目链接

做的第一道数位DP题，听说是最基础的模板题，但还是花了好长时间才写出来。。。。。

想深入了解下数位DP的请点这里

先设dp数组dp[i][j][k]表示数位是i，以j开头的数k出现的次数

有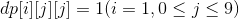 

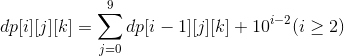
数位dp的题一般都会用到前缀数组，题目要求我们求b-a这个区间里各个数码出现的次数，我们可以分别求出（0，b）和（0,a-1）然后相减即可

具体分析请看代码，写的还算详细

 #include <bits/stdc++.h>
 using  namespace  std;
 typedef long long ll;
 ll dp[][][];
 ll ans[];//用来储存每个数码出现的次数
 ll bin[];//表示i位数中数码i出现的次数
 ll d[];//这个用来存储数的每一位
 void rule(){
     bin[]=;
     for(int i=;i<;i++) bin[i]=bin[i-]*;
     for(int i=;i<;i++) dp[][i][i]=;
     for(int i=;i<=;i++){
         for(int j=;j<=;j++){
             for(int z=;z<=;z++){
                 for(int k=;k<=;k++)
                 dp[i][j][z]+=dp[i-][k][z];//比如i=2,j=2时，所求数字范围应该是200-299,这一步把0-99中各数码出现次数加进去
                 dp[i][z][z]+=bin[i-];//这一位这是把200-299总共出现了100次的2给加进去
             }
         }
     }
 }
 void solve(ll x,int flag){
     ll tmpx=x;//存储传进来的x
     int cnt=;//记录x的位数
     memset(d,,sizeof(d));
     while(x){
         d[++cnt]=x%;
         x/=;
     }
     for(int i=;i<cnt;i++){//这一步是最高位为0的，这些数都不会受到x的上限限制，都可以直接加进来
         for(int j=;j<=;j++){
             for(int k=;k<=;k++)
             ans[k]+=dp[i][j][k]*flag;
         }
     }
     int tmpt=cnt;
     while(cnt){//可以举个456的例子来仔细分析一下
         for(int i=;i<d[cnt];i++){//注意这里是小于不是等于，保证上限不被取到，在后面再被处理
             if(!i&&cnt==tmpt) continue;//这种情况在最高位为0时已经统计过了，不能重复
             for(int j=;j<=;j++){
                     ans[j]+=dp[cnt][i][j]*flag;//不是上限的时候都直接加
             }
         }
         ans[d[cnt]]+=(tmpx%bin[cnt]+)*flag;cnt--;//随着while循环，上限一步步的被处理
     }//简述一下过程（456），就是第一个for处理了0-399，然后把首位4的57次加上，第二个for，处理的0-49......就这样一步步往下
 }
 int  main(){
   ll a,b;scanf("%lld%lld",&a,&b);
   rule();
   solve(b,);solve(a-,-);//1和-1是符号位，分别是加和减
   for(int i=;i<;i++)
   printf("%lld%c",ans[i],i==?'\n':' ');
   return ;
 }