[DeeplearningAI笔记]Batch NormalizationBN算法Batch归一化_02_3.4-3.7
Batch Normalization
Batch归一化
觉得有用的话,欢迎一起讨论相互学习~Follow Me
3.4正则化网络的激活函数
- Batch归一化会使你的参数搜索问题变得很容易,使神经网络对超参数的选择更加稳定.超参数的范围会更庞大,工作效果也更好.也会使你更容易的训练甚至是深层网络.
- 对于logistic回归来说
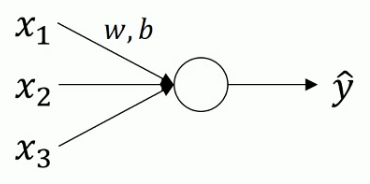
正则化原理
\[u=\frac{1}{m}\sum x^{i}(求出平均值u)\]\[x=x-u\] \[\sigma^{2}=\frac{1}{m}\sum(x^{i})^{2}(求出方差)\]\[x=\frac{x}{\sigma^{2}}\]
函数曲线会由类似于椭圆变成更圆的东西,更加易于算法优化.
- 深层神经网络
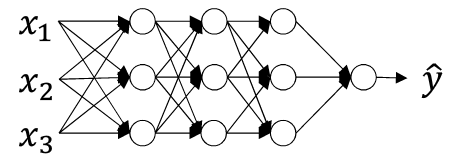
- 我们将每一层神经网络计算得到的z值(在计算激活函数之前的值)进行归一化处理,即将\(Z^{[L]}的值进行归一化处理,进而影响下一层W^{[L+1]}和b^{[L+1]}\)的计算.

- 此时z的每个分量都含有平均值0和方差1,但我们不想让隐藏单元总是含有平均值0和方差1,例如在应用sigmoid函数时,我们不想使其绘制的函数图像如图所示,我们想要变换方差或者是不同的平均值.


第L层神经元正则化公式
\[u=\frac{1}{m}\sum_{i}Z^{i}\]\[\sigma^{2}=\frac{1}{m}\sum_{i}(Z^{i}-u)^{2}\]\[Z^{i}_{norm}=\frac{Z^{i}-u}{\sqrt{\sigma^2+\epsilon}}\]\[\check{Z^{i}}=\gamma Z^{i}_{norm}+\beta \]
3.5 将Batch Normalization拟合进神经网络
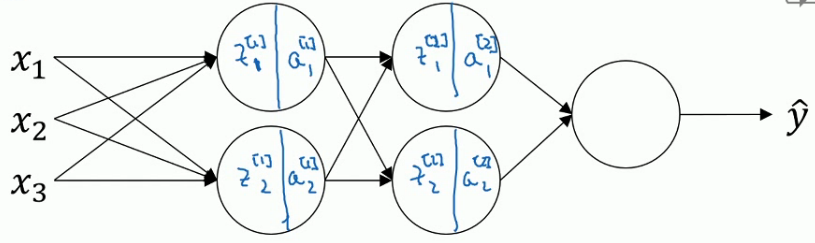
对于Batch Normalization算法而言,计算出一层的\(Z^{[l]}\)之后,进行Batch Normalization操作,次过程将有\(\beta^{[l]},\gamma^{[l]}\)这两个参数控制.这一步操作会给你一个新的规范化的\(z^{[l]}\)值.然后将其输入到激活函数中,得到\(a^{[l]}\)

实质上,BN算法是在每一层的\(Z^{[l]}\)和\(a^{[l]}\)之间进行的运算
3.6 Batch Normalization为什么奏效
原因一
- 无论数据的范围是0~1之间还是1~1000之间,通过归一化,所有的输入特征X,都可以获得类似范围的值,可加速学习.
原因二
- 如果神经元的数据分布改变,我们也许需要重新训练数据以拟合新的数据分布.这会带来一种数据的不稳定的效果.(covariate shift)
- Batch Normalization做的是它减少了这些隐藏值分布变化的数量.因为随着训练的迭代过程,神经元的值会时常发生变化.batch归一化可以确保,无论其怎样变化,其均值和方差将保持不变.(由每一层的BN函数的参数\(\beta^{[l]},\gamma^{[l]}\)决定其方差和均值)
- Batch Normalization减少了输入值改变的问题,它的确使这些值变的稳定,即是原先的层改变了,也会使后面的层适应改变的程度减小.也可以视为它减少了前层参数和后层参数之间的联系.
原因三
- Batch Normalization有轻微的正则化作用.
- BN算法是通过mini-batch计算得出,而不是使用整个数据集,所以会引入部分的噪音,即会在纵轴上有些许波动.
- 缩放的过程从\(Z^{[l]}\rightarrow\check{Z^{[l]}}\)也会引入一些噪音.
- 所以和Dropout算法一样,它往每个隐藏层的激活值上增加了噪音,dropout有噪音的模式,它使一个隐藏的单元以一定的概率乘以0,以一定得概率乘以1.BN算法的噪音主要体现在标准偏差的缩放和减去均值带来的额外噪音.这使得后面层的神经单元不会过分依赖任何一个隐藏单元.有轻微的正则化作用.如果你想获得更好的正则化效果,可以在使用Batch-Normalization的同时使用Dropout算法.
3.7测试时的Batch Normalization
- Batch-Normalization将你的数据以mini-batch的形式逐一处理,但在测试时,你可能需要对每一个样本逐一处理.我们应该怎么做呢~
Batch-Normalization公式
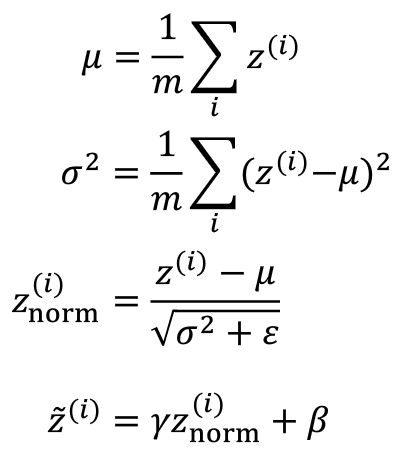
- 注意 对于u和\(\sigma\)是在整个mini-batch上进行计算,但是在测试时,你不会使用一个mini-batch中的所有数据(因为测试时,我们仅仅需要少量数据来验证神经网络训练的正确性即可.)况且如果我们只使用一个数据,那一个样本的均值和方差没有意义,因此我们需要用其他的方式来得到u和\(\sigma\)这两个参数.
- 运用覆盖所有mini-batch的指数加权平均数来估算u和\(\sigma\)
利用指数加权平均来估算\(u和\sigma\)对数据进行测试
对于第L层神经元层,标记mini-batch为\(x^{[1]},x^{[2]},x^{[3]},x^{[4]}...x^{[n]}\)在训练这个隐藏层的第一个mini-batch得到\(u^{[1][l]}\),训练第二个mini-batch得到\(u^{[2][l]}\),训练第三个mini-batch得到\(u^{[3][l]}\)...训练第n个mini-batch得到\(u^{[n][l]}\).然后利用指数加权平均法估算\(u\)的值,同理,以这种方式利用指数加权平均的方法估算\(\sigma^{2}\).
总结
在训练时,u和\(\sigma^{2}\)在整个mini-batch上计算出来的,但是在测试时,我们需要单一估算样本,方法是根据你的训练集估算u和\(\sigma^{2}\).常见的方法有利用指数加权平均进行估算.
[DeeplearningAI笔记]Batch NormalizationBN算法Batch归一化_02_3.4-3.7的更多相关文章
- Batch Normalization原理及其TensorFlow实现——为了减少深度神经网络中的internal covariate shift,论文中提出了Batch Normalization算法,首先是对”每一层“的输入做一个Batch Normalization 变换
批标准化(Bactch Normalization,BN)是为了克服神经网络加深导致难以训练而诞生的,随着神经网络深度加深,训练起来就会越来越困难,收敛速度回很慢,常常会导致梯度弥散问题(Vanish ...
- 转载: scikit-learn学习之K-means聚类算法与 Mini Batch K-Means算法
版权声明:<—— 本文为作者呕心沥血打造,若要转载,请注明出处@http://blog.csdn.net/gamer_gyt <—— 目录(?)[+] ================== ...
- 吴恩达深度学习笔记(七) —— Batch Normalization
主要内容: 一.Batch Norm简介 二.归一化网络的激活函数 三.Batch Norm拟合进神经网络 四.测试时的Batch Norm 一.Batch Norm简介 1.在机器学习中,我们一般会 ...
- 聚类K-Means和大数据集的Mini Batch K-Means算法
import numpy as np from sklearn.datasets import make_blobs from sklearn.cluster import KMeans from s ...
- Python机器学习笔记:K-Means算法,DBSCAN算法
K-Means算法 K-Means 算法是无监督的聚类算法,它实现起来比较简单,聚类效果也不错,因此应用很广泛.K-Means 算法有大量的变体,本文就从最传统的K-Means算法学起,在其基础上学习 ...
- [DeeplearningAI笔记]神经网络与深度学习2.11_2.16神经网络基础(向量化)
觉得有用的话,欢迎一起讨论相互学习~Follow Me 2.11向量化 向量化是消除代码中显示for循环语句的艺术,在训练大数据集时,深度学习算法才变得高效,所以代码运行的非常快十分重要.所以在深度学 ...
- 机器学习实战笔记-k-近邻算法
机器学习实战笔记-k-近邻算法 目录 1. k-近邻算法概述 2. 示例:使用k-近邻算法改进约会网站的配对效果 3. 示例:手写识别系统 4. 小结 本章介绍了<机器学习实战>这本书中的 ...
- Java基础复习笔记基本排序算法
Java基础复习笔记基本排序算法 1. 排序 排序是一个历来都是很多算法家热衷的领域,到现在还有很多数学家兼计算机专家还在研究.而排序是计算机程序开发中常用的一种操作.为何需要排序呢.我们在所有的系统 ...
- 算法笔记_071:SPFA算法简单介绍(Java)
目录 1 问题描述 2 解决方案 2.1 具体编码 1 问题描述 何为spfa(Shortest Path Faster Algorithm)算法? spfa算法功能:给定一个加权连通图,选取一个 ...
随机推荐
- linux 安装MySql 5.7.21 操作步骤
一:到mysql官网下载最新的mysql包 mysql-5.7.21-linux-glibc2.12-x86_64 https://dev.mysql.com/downloads/mysql/ 二:在 ...
- Object.keys、Object.getOwnPropertyNames区别
用途 Object.keys 定义:返回一个对象可枚举属性的字符串数组: Object.getOwnPropertyNames 定义:返回一个对象可枚举.不可枚举属性的名称: 属性的可枚举性.不可枚举 ...
- [bzoj1227] [SDOI2009]虔诚的墓主人
终于填上了这个万年巨坑....从初二的时候就听说过这题...然后一直不敢写QAQ 现在感觉也不是很烦(然而我还是写麻烦了 离散化一波,预处理出组合数什么的.. 要维护对于当前行,每列上方和下方节点凑出 ...
- hdu_1027(好吧。。。牛。。。next_permutation也可以水过)
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; ; int ...
- vuex使用心得分享(填坑)
今天我们简单说一下vuex的使用,vuex是什么呢,相当于react的redux,如果项目使用数据过多的话,直接管理是非常不方便的,那么采用vuex,那些繁琐的问题就迎刃而解了,首先我们先看看官方对v ...
- webpack+vue项目实战(四,前端与后端的数据交互和前端展示数据)
地址:https://segmentfault.com/a/1190000010063757 1.前言 今天要做的,就是在上一篇文章的基础上,进行功能页面的开发.简单点说呢,就是与后端的数据交互和怎么 ...
- LNMP环境的搭建
http://blog.csdn.net/wzy_1988/article/details/8438355#
- 【开发技术】如何查看项目中struts的版本
struts-configer.xml(struts1)或struts.xml(struts2)中 struts-2.0.dtd处表示版本号
- windows安装xampp时出现,unable to realloc xxxxxxxx bytes
摘录自:http://blog.csdn.net/lz610756247/article/details/70842166 Windows虚拟内存的设置 问题描述:由于开启虚拟内存会导致硬盘IO性能下 ...
- 新装Centos7.2 配置防火墙
1.安装 yum -y install firewalld2.开机启动 systemctl enable firewalld3.设置防火墙规则 systemctl restart firewalld ...
