hdu 2865 Polya计数+(矩阵 or 找规律 求C)

Birthday Toy

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 644    Accepted Submission(s): 326

Problem Description

AekdyCoin loves toys. It is AekdyCoin’s Birthday today and he gets a special “Toy”.
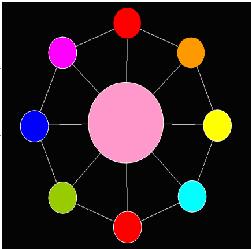
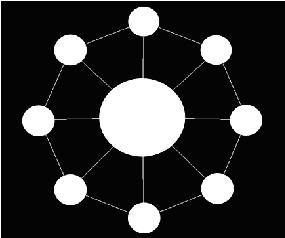
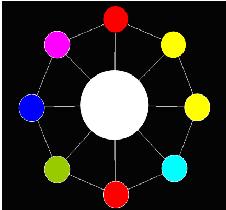
The “Toy” is in bulk and AekdyCoin has to make one by him. Let’s assume that the “Toy” has N small white beads and one Big bead .If someone want to make a “Toy”, he (or she) must always puts the Big bead in center, and then connect the other N small beads around it by using N sticks with equal length, and then the N small beads must be connected by N sticks with equal length, and it could be seen as a regular polygon. Figure 1 shows a “Toy” with 8 small white beads and one big white bead.

Now AekdyCoin has C kinds of available color, say blue, green, yellow, pink …etc. He wants to color these beads, but he thinks that must be too boring and stupid. So he colors these beads with one role: any adjacent beads couldn’t have same color. Figure 2 shows a legal situation, and Figure 3 shows an illegal situation.


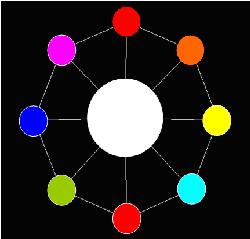
It seems that the “Toy” becomes more interesting for AekdyCoin right now; however, he wants to color the big bead in center. Of course, he should follow the role above.

Now AekdyCoin begins to play with the “Toy”, he always colors the big beads and then the other small beads. He should color under the rule above. After several minutes, AekdyCoin finally makes a perfect “Toy”. Figure 4 shows a situation that is under the color rule.

AekdyCoin now want to know the different method to color the “Toy” whit at most K color. (“Toy” contains N small beads and one big bead.)
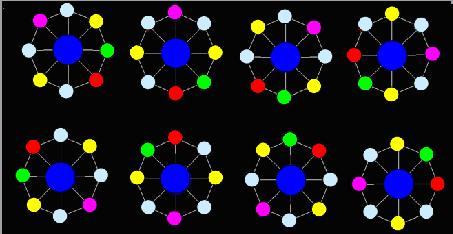
But, no, the problem is not so easy .The repetitions that are produced by rotation around the center of the circular necklace are all neglected. Figure 5 shows 8 “Toy”, they are regard as one method.

Now AekdyCoin will give you N and K, he wants you to help him calculate the number of different methods, because the number of method is so huge, so AekdyCoin just want you to tell him the remainder when divided by M.
In this problem, M = 1,000,000,007.

 

Input

The input consists of several test cases.(at least 1000)
Every case has only two integers indicating N, K 
(3<=N<=10^9, 4<=K<=10^9)

 

Output

For each case, you should output a single line indicates the remainder of number of different methods after divided by M.

 

Sample Input

3 4
3 5
3 17
162 78923

 

Sample Output

8
40
19040
19469065

 

/*
hdu 2865 Polya计数+(矩阵 or 找规律 求C)
 
给你n个小球全部连在一个大球上然后对他们进行染色，要求相连的球颜色不一样
首先确定大球为一种颜色(k种可能)。然后用剩下k-1种用Polya去处理小球即可
 
在计算循环节长度为i的可能数时由于k很大,矩阵快速幂很明显不行诶
1.可以考虑递推,假设第一个颜色是x,用f[i][1]表示当前颜色是x,f[i][0]表示当前颜色非x。
f[i][1] = f[i-1][0]
f[i][0] = (k-2)*f[i-1][0]+(k-1)*f[i-1][1]
 
2.假设用3种颜色染循环节长度为len小球,构建出来的矩阵是
0 1 1     2 1 1      2 3 3      6 5 5    10 11 11
1 0 1 ->  1 2 1  ->  3 2 3  ->  5 6 5 -> 11 10 11
1 1 0     1 1 2      3 3 2      5 5 6    11 11 10
——参考自cxlove大神.
可以发现是有规律的：(2 = 3-1)
n = 1  ->   0   (2^n - 2)
n = 2  ->   6   (2^n + 2)
n = 3  ->   6   (2^n - 2)
n = 4  ->   18  (2^n + 2)
n = 5  ->   30  (2^n - 2)
代码为注释部分
 
hhh-2016-04-22 10:12:35
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <functional>
using namespace std;
#define lson  (i<<1)
#define rson  ((i<<1)|1)
typedef long long ll;
using namespace std;
const ll mod = 1e9 + 7;
const int  maxn = 40010;
 
int num;
int prime[maxn];
int isPrime[maxn];
 
void get_prime()
{
    num = 0;
    memset(isPrime,0,sizeof(isPrime));
    for(int i = 2; i <= maxn-10; i++)
    {
        if(!isPrime[i])
        {
            prime[num++] = i;
            for(int j = i+i; j <= maxn-10; j+=i)
                isPrime[j] = 1;
        }
    }
}
 
ll euler(ll cur)
{
    ll ans = cur;
    ll x = cur;
    for(int i = 0; i < num && prime[i]*prime[i] <= cur; i++)
    {
        if(x % prime[i] == 0)
        {
            ans = ans/prime[i]*(prime[i]-1);
            while(x % prime[i] == 0)
                x /= prime[i];
        }
    }
    if(x > 1)
    {
        ans = ans/x*(x-1);
    }
    return ans%mod;
}
 
ll pow_mod(ll a,ll n)
{
    ll ret = 1;
    a %= mod;
    while(n)
    {
        if(n & 1) ret = ret*a%mod;
        a = a*a%mod;
        n >>= 1;
    }
    return ret%mod;
}
 
/*
another:
ll solve(ll p,ll k)
{
    ll ans=pow_mod(p-1,k);
    if(k&1)
        ans=(ans+mod-(p-1))%mod;
    else
        ans=(ans+p-1)%mod;
    return ans;
}
*/
 
struct Matrix
{
    ll ma[3][3];
    Matrix()
    {
        memset(ma,0,sizeof(ma));
    }
};
 
Matrix mult(Matrix ta,Matrix tb)
{
    Matrix tc;
    for(int i = 0 ; i < 2; i ++)
    {
        for(int j = 0; j < 2; j++)
        {
            for(int k = 0; k < 2; k++)
                tc.ma[i][j] = (tc.ma[i][j] + ta.ma[i][k]*tb.ma[k][j]%mod)%mod;
        }
    }
    return tc;
}
 
Matrix Mat_mod(Matrix a,int n)
{
    Matrix cnt;
    for(int i = 0; i < 2; i++)
        cnt.ma[i][i] = 1;
    while(n)
    {
        if(n & 1 ) cnt = mult(cnt,a);
        a = mult(a,a);
        n >>= 1;
    }
    return cnt;
}
 
Matrix mat;
Matrix begi;
 
ll solve(ll p,ll k)
{
    begi.ma[0][1] = 1,begi.ma[0][0] = 0,begi.ma[1][0] = 0,begi.ma[1][1] = 0;
    mat.ma[0][0] = p - 2, mat.ma[1][0] = p - 1, mat.ma[0][1] = 1, mat.ma[1][1] = 0;
    mat = Mat_mod(mat,k-1);
    Matrix tp = mult(begi,mat);
    return p*tp.ma[0][0]%mod;
}
 
ll cal(ll  n,ll k)
{
    ll ans = 0;
    for(int i = 1; i*i <= n; i++)
    {
        if(n % i == 0)
        {
            ans = (ans + solve(k,n/i)*euler(i)%mod)%mod;
            if(n != i*i)
                ans = (ans + solve(k,i)*euler(n/i)%mod)%mod;
        }
    }
    return (ans*pow_mod(n,mod-2))%mod;
}
 
ll N,k;
 
int main()
{
    get_prime();
    while(scanf("%I64d%I64d",&N,&k) != EOF)
    {
        printf("%I64d\n",k*cal(N,k-1)%mod);
    }
    return 0;
}