6_6 小球下落（UVa679）<完全二叉树编号>

有K个球从一完整二叉树（fully binary tree，FBT）的树根（root）一个一个往下掉。当这个球遇到非终端节点时，可能往左子树跑，也可能往右子树跑，如此直到这颗球到达终端节点（也就是树叶）为止。至于在非终端节点时球该往左或往右的决定乃是由2个值true，false来控制的。如果这非终端节点的现在的值为false，则球来的时候会往左子树走，但是这个值会变为true。如果这非终端节点的现在的值为true，则球来的时候会往右子树走，但是这个值会变为false。请注意：一开始时所有非终端节点的值均为false。另外，在完整二叉树中所有的节点被依序编号，从上（深度= 1）到下，由左到右。请参考下图。

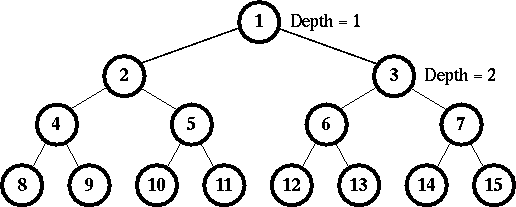
举例来说，上面的图为深度为4的完整二叉树。第一颗球往下掉会经过节点1、2、4最后落在节点8中。第二颗球往下掉则会经过节点1、3、6最后落在节点12中。第三颗球往下掉会经过节点1、2、5最后落在节点10中。
给你完整二叉树的深度D以及落下的第I个球，请你写一个程序算出第I个球落在终端节点的编号。

Input
输入的第一列有一个整数，代表以下有几组测试数据。
每组测试数据一列有2个整数D，I（2 <= D <= 20，1 <= I <= 524288）。你可以假设I不会超过终端节点的数目。
Output
对每组测试数据输出一列，第I个球落在终端节点的编号。

Sample Input
5
4 2
3 4
10 1
2 2
8 128
-1

Sample Output
12
7
512
3
255