第二十四篇 玩转数据结构——队列（Queue）

 

 

 

1.. 队列基础

• 队列也是一种线性结构；

• 相比数组，队列所对应的操作数是队列的子集；

• 队列只允许从一端（队尾）添加元素，从另一端（队首）取出元素；

• 队列的形象化描述如下图：
• 
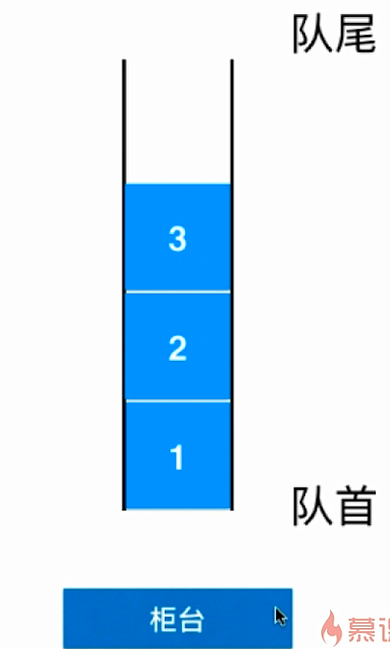
• 队列是一种先进先出（First In First Out）的数据结构；

2.. 队列的实现

• 任务目标如下：

• Queue<E>
  ·void enqueue(E)   //入队
  ·E dequeue()   //出队
  ·E getFront()  //查看队首元素
  ·int getSize()   //查看队列中元素的个数
  ·boolean isEmpty()   //查看队列是否为空

• 需要提一下，从用户的角度来看，只要实现上述操作就好，具体底层实现，用户并不关心，实际上，底层确实有多种实现方式。
• 我们准备在之前实现的动态数组基础上，来实现"队列"这种数据结构。
• 先定义一个接口Interface，如下：

• public interface Queue<E> {
      int getSize();
  
      boolean isEmpty();
  
      void enqueue(E e);
  
      E dequeue();
  
      E getFront();
  
  }

• 实现基于Array类的ArrayQueue类，并进行测试：

• public class ArrayQueue<E> implements Queue<E> {
      private Array<E> array;
  
      //构造函数
      public ArrayQueue(int capacity) {
          array = new Array<>(capacity);
      }
  
      //无参数构造函数
      public ArrayQueue() {
          array = new Array<>();
      }
  
      //实现getSize()方法
      @Override
      public int getSize() {
          return array.getSize();
      }
  
      //实现isEmpty方法
      @Override
      public boolean isEmpty() {
          return array.isEmpty();
      }
  
      //实现getCapacity方法
      public int getCapacity() {
          return array.getCapacity();
      }
  
      //实现enqueue方法
      @Override
      public void enqueue(E e) {
          array.addLast(e);
      }
  
      //实现dequeue方法
      @Override
      public E dequeue() {
          return array.removeFirst();
      }
  
      //实现getFront方法
      @Override
      public E getFront() {
          return array.getFirst();
      }
  
      //方便打印测试
      @Override
      public String toString() {
          StringBuilder res = new StringBuilder();
          res.append("Queue: ");
          res.append("front [");
          for (int i = ; i < array.getSize(); i++) {
              res.append(array.get(i));
              if (i != array.getSize() - ) {
                  res.append(", ");
              }
          }
          res.append("] tail");
          return res.toString();
      }
  
    // 测试
      public static void main(String[] args){
          ArrayQueue<Integer> queue = new ArrayQueue<>();
  
          // 测试入队
          for(int i=;i<;i++){
              queue.enqueue(i);
          }
          System.out.println(queue);
  
          // 测试出队
          queue.dequeue();
          System.out.println(queue);
      }
  }

• 输出结果：

• Queue: front [, , , , ] tail
  Queue: front [, , , ] tail

3.. 数组队列的时间复杂度分析：

• ArrayQueue<E>
  ·void enqueue(E)   O()    均摊
  ·E dequeue()   O(n)
  ·E getFront()  O()
  ·int getSize()   O()
  ·boolean isEmpty()   O()

4.. 循环队列

• 数组队列的出队操作的复杂度是O(n)，性能很差，解决方法就是使用循环队列（Loop Queue）
• 循环队列的示意图如下：
• 
• 
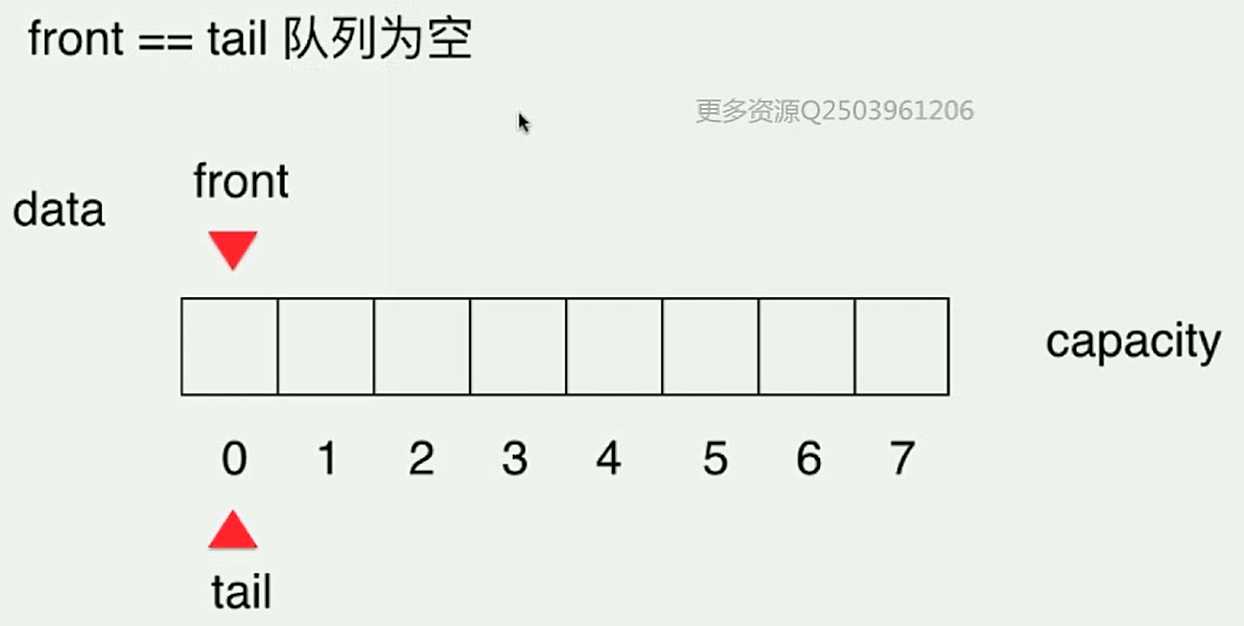
• 实现循环队列的业务逻辑，并进行测试：

• public class LoopQueue<E> implements Queue<E> {
  
      private E[] data;
      private int front, tail;
      private int size;
  
      //构造函数
      public LoopQueue(int capacity) {
          data = (E[]) new Object[capacity + ];
          front = ;
          tail = ;
          size = ;
      }
  
      //无参数构造函数
      public LoopQueue() {
          this(); //直接调用有参数的构造函数，然后传入一个默认值
      }
  
      //实现getCapacity方法
      public int getCapacity() {
          return data.length - ;
      }
  
      //实现isEmpty方法
      @Override
      public boolean isEmpty() {
          return front == tail;
      }
  
      //实现getSize方法
      @Override
      public int getSize() {
          return size;
      }
  
      //实现enqueue方法
      @Override
      public void enqueue(E e) {
          //判断队列是否已满
          if ((tail + ) % data.length == front) {
              resize(getCapacity() * );
          }
  
          data[tail] = e;
          tail = (tail + ) % data.length;
          size++;
      }
  
      //实现dequeue方法
      @Override
      public E dequeue() {
          //判断队列是否为空
          if (isEmpty()) {
              throw new IllegalArgumentException("Cannot dequeue from an empty queue.");
          }
  
          E ret = data[front];
          data[front] = null;
          front = (front + ) % data.length;
          size--;
  
          if (size == getCapacity() /  && getCapacity() /  != ) {
              resize(getCapacity() / );
          }
          return ret;
      }
  
      //实现getFront方法
      @Override
      public E getFront() {
          if (isEmpty()) {
              throw new IllegalArgumentException("Queue is empty.");
          }
          return data[front];
      }
  
      //实现resize方法
      private void resize(int newCapacity) {
          E[] newData = (E[]) new Object[newCapacity + ];
          for (int i = ; i < size; i++) {
              newData[i] = data[(i + front) % data.length];
          }
          data = newData;
          front = ;
          tail = size;
      }
  
      //方便打印测试
      @Override
      public String toString() {
          StringBuilder res = new StringBuilder();
          res.append(String.format("Queue: size=%d, capacity=%d\n", size, getCapacity()));
          res.append("front [");
          for (int i = front; i != tail; i = (i + ) % data.length) {
              res.append(data[i]);
              if ((i + ) % data.length != tail) {
                  res.append(", ");
              }
          }
          res.append("] tail");
          return res.toString();
      }
  
      //测试
      public static void main(String[] args) {
          LoopQueue<Integer> queue = new LoopQueue<>();
  
          // 测试入队
          for (int i = ; i < ; i++) {
              queue.enqueue(i);
          }
          System.out.println(queue);
  
          // 测试出队
          queue.dequeue();
          System.out.println(queue);
      }
  }

• 输出结果：

• Queue: size=, capacity=
  front [, , , , ] tail
  Queue: size=, capacity=
  front [, , , ] tail

5.. 循环队列的复杂度分析

• LoopQueue<E>
  ·void enqueue(E)   O()    均摊
  ·E dequeue()   O()   均摊
  ·E getFront()  O()
  ·int getSize()   O()
  ·boolean isEmpty()   O()

6.. 使用简单算例测试ArrayQueue与LoopQueue的性能差异

• import java.util.Random;
  
  public class Main {
  
      // 测试使用q运行opCount个enqueue和dequeue操作所需要的时间，单位：秒
      private static double testQueue(Queue<Integer> q, int opCount) {
          long startTime = System.nanoTime();
  
          Random random = new Random();
          for (int i = ; i < opCount; i++) {
              q.enqueue(random.nextInt(Integer.MAX_VALUE));
          }
          for (int i = ; i < opCount; i++) {
              q.dequeue();
          }
  
          long endTime = System.nanoTime();
          return (endTime - startTime) / 1000000000.0;
      }
  
      public static void main(String[] args) {
  
          int opCount = ;
  
          ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();
          double time1 = testQueue(arrayQueue, opCount);
          System.out.println("ArrayQueue, time: " + time1 + " s");
  
          LoopQueue<Integer> loopQueue = new LoopQueue<>();
          double time2 = testQueue(loopQueue, opCount);
          System.out.println("LoopQueue, time: " + time2 + " s");
  
      }
  }

• 输出结果

• ArrayQueue, time: 2.88077896 s
  LoopQueue, time: 0.01140229 s