1维FDTD仿真
FDTD基本原理是把麦克斯韦方程胡两个矢量旋度方程写成差分形式,利用数值方法求其解。
假设电磁场传播方向为x轴方向,电场只有z轴方法分量,磁场只有y轴方向分量。两个旋度方程可以写成下列形式


电场、磁场写成下在形式

连续方程写成差分形式




其中的常数项因子

其中 为自由空间特性阻抗377欧姆,令
为自由空间特性阻抗377欧姆,令 ,递推关系如下图
,递推关系如下图

实现时可用下图表示

从而得到差分递推方程如下
hy(mm) = hy(mm) + (ez(mm+1)- ez(mm))/imp0;
ez(mm) = ez(mm) + (hy(mm)- hy(mm-1))*imp0;
%1D FDTD with source
SIZE = 200;
ez = zeros(1,SIZE);
hy = zeros(1,SIZE);
imp0=377.0;
maxTime = 10000;
for qTime = 0 : 1 : maxTime
for mm = 1 : 1 : SIZE -1
hy(mm) = hy(mm) + (ez(mm+1)- ez(mm))/imp0;
end
figure(1); t_hy = plot(hy);
title('Magnetic Field');
for mm = 2 : 1 : SIZE
ez(mm) = ez(mm) + (hy(mm)- hy(mm-1))*imp0;
end
figure(2); t_ez = plot(ez);
title('Electric Field')
ez(50) = ez(50) + exp(-(qTime-30.0)*(qTime-30.0)/100.0);
% pause(0.01);
% % refreshdata(t_hy);
% refreshdata(t_ez);
% drawnow;
end 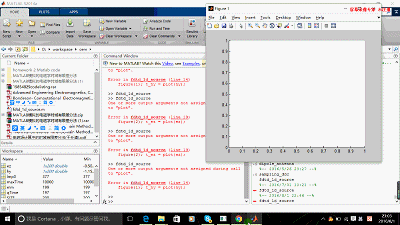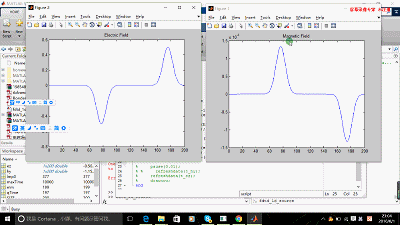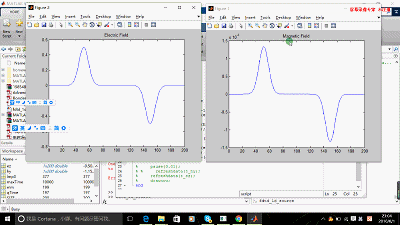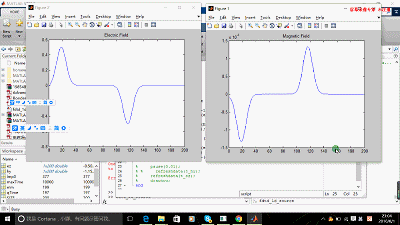
1维FDTD仿真的更多相关文章
- 基于SILVACO ATLAS的a-IGZO薄膜晶体管二维器件仿真(01)
最近因为肺炎的缘故,宅在家里不能出门,就翻了下一些资料,刚好研究方向是这个,就简单研究了下.参考资料主要如下: 1.<半导体工艺和器件仿真软件Silvaco TCAD实用教程> 唐龙谷 2 ...
- 基于SILVACO ATLAS的a-IGZO薄膜晶体管二维器件仿真(07)
今天主要解决一下defect语句: defect region=1 nta=1.55e20 wta=0.013 wtd=0.12 ngd=6.5e16 wga=2 ntd=1.55e20 ngd=0 ...
- 基于SILVACO ATLAS的a-IGZO薄膜晶体管二维器件仿真(06)
在知网看到了江南大学的硕士论文: 双有源层a-IGZO薄膜晶体管的特性仿真 IGZO/IZO双有源层薄膜晶体管特性的模拟研究 发现,我昨天的文章中参数的设置存在重大失误,如下材料定义语句中: mate ...
- 基于SILVACO ATLAS的a-IGZO薄膜晶体管二维器件仿真(04)
在eetop上有好多好东西啊: Silvaco_TCAD_中文教程1 不过这个教程里是Linux系统的,而且工艺仿真占了比较大的篇幅. defect region=1 nta=5e17 wta=0.1 ...
- 基于SILVACO ATLAS的a-IGZO薄膜晶体管二维器件仿真(02)
Silvaco的破解用了好久好久,而且之后拷了上次例子的代码,Tonyplot的输出存在报错,还是四连. 当然这个点一下还是会出图的.但是,源代码稍微改了下结构,又有报错,而且程序直接终止. go a ...
- 基于SILVACO ATLAS的a-IGZO薄膜晶体管二维器件仿真(08)
进展比较慢啊... 根据江南大学硕士论文IGZO/IZO双有源层薄膜晶体管特性的模拟研究: 其中, gCBa:类受主导带尾态 gVBd:类施主价带尾态 gGd:类施主氧空位态 NDeep:价带尾深施主 ...
- 基于SILVACO ATLAS的a-IGZO薄膜晶体管二维器件仿真(05)
关于特性曲线的输出调整: 初代版本 material material=igzo eg300=3.5 nc300=8.5e21 nv300=8.5e21 taun0=1e-9 taup0=1e-9 a ...
- 基于SILVACO ATLAS的a-IGZO薄膜晶体管二维器件仿真(03)
今天逛ResearchGate的时候发现了一个不错的Atlas入门教程:Step by step with ATLAS Silvaco点击链接免费下载.. Atlas代码结构 当然可能有一点太基础了. ...
- PCB仿真软件与电磁场求解器的算法
1. 简介 目前商业化的PCB仿真软件主要有: Cadence公司的Sigrity.Ansys公司的SIwave/HFSS.CST公司的CST.Mentor公司的HyperLynx.Polor公司的S ...
随机推荐
- Win7如何部署apache服务器(包括SSL设置)
部署普通站点 1.首先下载apache24版本,下载地址为http://pan.baidu.com/s/1pLmvDgB; 2.解压到你的电脑本地目录,如D:\Apache24(下文配置都会以当前目录 ...
- 创建WCF服务寄宿到IIS
一.WCF简介: Windows Communication Foundation(WCF)是由微软开发的一系列支持数据通信的应用程序框架,可以翻译为Windows 通讯开发平台. 整合了原有的win ...
- javascript的 == 与 === 的区别
1.对于基础类型,例如string,number ==和===是有区别的 1)不同类型间比较,==之比较“转化成同一类型后的值”看“值”是否相等,===如果类型不同,其结果就是不等 2)同类型比较,直 ...
- 最小生成树Prim算法(邻接矩阵和邻接表)
最小生成树,普利姆算法. 简述算法: 先初始化一棵只有一个顶点的树,以这一顶点开始,找到它的最小权值,将这条边上的令一个顶点添加到树中 再从这棵树中的所有顶点中找到一个最小权值(而且权值的另一顶点不属 ...
- 从" ThinkPHP 开发规范 "看 PHP 的命名规范和开发建议
稍稍水一篇博客,摘抄自Think PHP 的开发规范,很有引导性,我们可以将这些规范实践到原生 PHP 中. 命名规范 使用ThinkPHP开发的过程中应该尽量遵循下列命名规范: 类文件都是以.cla ...
- DOM LOAD测试笔记
DOM时间:1823ms LOAD时间:4912ms COMP时间:5427ms 1585 4757 5650 1859 3487 3910 1600 4648 5099 1610 4428 4878 ...
- java调用html模板发送html内容的邮件
在项目需要发送邮件,普通内容的邮件觉得太单调.太丑,没逼格,所以说直接把用到的邮件内容做成一个html模板,发送之前将对应参数替换掉,发送html内容的高逼格邮件. 首先需要引用jar包,这就不多说了 ...
- How to Use Telnet to Test SMTP Communication
Topic Last Modified: 2005-05-24 Telnet is an extremely useful tool for troubleshooting issues relate ...
- 发布的时候Archive灰色
主要是因为发布的时候要选为将模拟器选择一下,选为Generic iOS Device. 来自为知笔记(Wiz)
- 【读书笔记】iOS-GCD-多线程编程
一,现在一个物理的CPU芯片实际上有64个(64核)CPU,如果1个CPU核虚拟为两个CPU核工作,那么一台计算机上使用多个CPU核就是理所当然的事了.尽管如此,“1个CPU核执行的CPU命令为一条无 ...
