hdu 1817 Necklace of Beads (polya)

Necklace of Beads

Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1049    Accepted Submission(s): 378

Problem Description

Beads of red, blue or green colors are connected together into a circular necklace of n beads ( n < 40 ). If the repetitions that are produced by rotation around the center of the circular necklace or reflection to the axis of symmetry are all neglected, how many different forms of the necklace are there?

 

Input

The input has several lines, and each line contains the input data n.
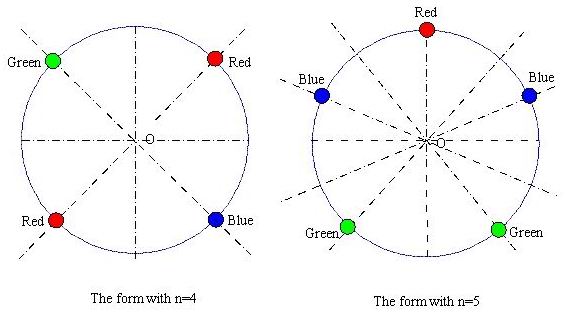
-1 denotes the end of the input file.

 

Output

The output should contain the output data: Number of different forms, in each line correspondent to the input data.

Sample Input
4
5
-1
 

Sample Output
21
39

help

C/C++:

 #include <map>
 #include <queue>
 #include <cmath>
 #include <vector>
 #include <string>
 #include <cstdio>
 #include <cstring>
 #include <climits>
 #include <iostream>
 #include <algorithm>
 #define INF 0x3f3f3f3f
 #define LL long long
 using namespace std;
 const int MAX = 1e5 + ;

 __int64 sum, n;

 __int64 gcd(__int64 a, __int64 b)
 {
     if (b == ) return a;
     return gcd(b, a%b);
 }

 __int64 my_pow(__int64 a, __int64 m)
 {
     __int64 ans = ;
     while (m)
     {
         if (m & ) ans *= a;
         a *= a;
         m >>= ;
     }
     return ans;
 }

 int main()
 {
     while (scanf("%I64d", &n), n != -)
     {
         sum = ;
         if (n <= )
         {
             printf("0\n");
             continue;
         }
         for (__int64 i = ; i <= n; ++ i)
         {
             __int64 temp = gcd(i, n);
             sum += my_pow(, temp);
         }
         if (n & )
             sum += n * my_pow(, (n + ) >> );
         else
         {
             sum += (n >> ) * my_pow(, (n + ) >> );
             sum += (n >> ) * my_pow(, n >> );
         }
         printf("%I64d\n", sum /  / n);
     }
     return ;
 }