leetcode算法笔记：二叉树，动态规划和回溯法

前言

写的比较匆忙，测试用例是能全部跑通的，不过考虑内存和效率的话，还有许多需要改进的地方，所以请多指教

在二叉树中增加一行

题目描述

给定一个二叉树，根节点为第1层，深度为 1。在其第 d 层追加一行值为 v 的节点。

添加规则：给定一个深度值 d （正整数），针对深度为 d-1 层的每一非空节点 N，为 N 创建两个值为 v 的左子树和右子树。

将 N 原先的左子树，连接为新节点 v 的左子树；

将 N 原先的右子树，连接为新节点 v 的右子树。

如果 d 的值为 1，深度 d - 1 不存在，则创建一个新的根节点 v，原先的整棵树将作为 v 的左子树。

Example

Input:
A binary tree as following:
       4
     /   \
    2     6
   / \   /
  3   1 5   

v = 1

d = 2

Output:
       4
      / \
     1   1
    /     \
   2       6
  / \     /
 3   1   5  

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/add-one-row-to-tree

 

基本思想

二叉树的先序遍历 

 

代码的基本结构

不是最终结构，而是大体的结构

/**
 * @param {number} cd:current depth,递归当前深度
 * @param {number} td:target depth, 目标深度
 */
var traversal = function (node, v, cd, td) {
    // 递归到目标深度，创建新节点并返回
  if (cd === td) {
    // return 新节点
  }
  // 向左子树递归
  if (node.left) {
    node.left = traversal (node.left, v, cd + 1, td);
  }
  // 向右子树递归
  if (node.right) {
    node.right = traversal (node.right, v, cd + 1, td);
  }
  // 返回旧节点
  return node;
};
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} v
 * @param {number} d
 * @return {TreeNode}
 */
var addOneRow = function (root, v, td) {
    // 从根节点开始递归
  traversal (root, v, 1, td);
  return root;
};

具体分析

我们可以分类讨论，分三种情况处理

 

第1种情况：目标深度<=当前递归路径的最大深度 

处理方法：val节点替换该目标深度对应的节点，并且

• 如果目标节点原来是左子树，那么重置后目标节点是val节点的左子树

• 如果目标节点原来是右子树，那么重置后目标节点是val节点的右子树

第2种情况：目标深度>当前递归路径的最大深度

阅读题目发现，有这么一个描述：“输入的深度值 d 的范围是：[1，二叉树最大深度 + 1]”

所以呢，当目标深度恰好比当前路径的树的深度再深一层时，处理方式是：

在最底下那一层节点的左右分支新增val节点

第3种情况：目标深度为1

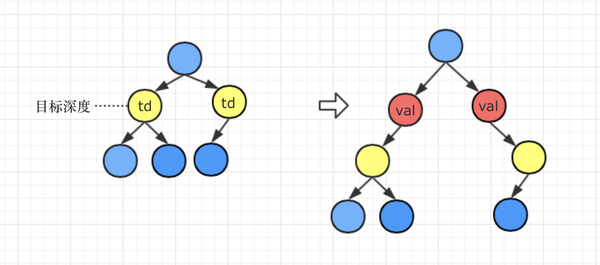
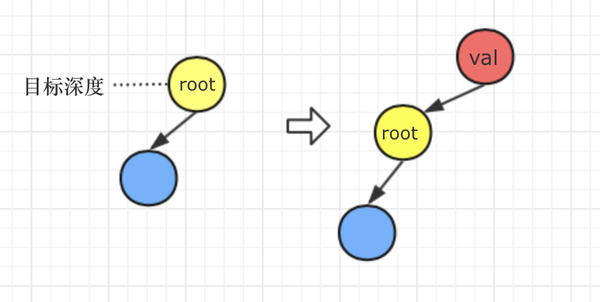
我们再分析题意，题目里说：“如果 d 的值为 1，深度 d - 1 不存在，则创建一个新的根节点 v，原先的整棵树将作为 v 的左子树。”

这说明当：目标深度为1时，我们的处理方式是这样的 

全部代码 

/**
 * @param {v} val,插入节点携带的值
 * @param {cd} current depth,递归当前深度
 * @param {td} target depth, 目标深度
 * @param {isLeft}  判断原目标深度的节点是在左子树还是右子树
 */
var traversal = function (node, v, cd, td, isLeft) {
  debugger;
  if (cd === td) {
    const newNode = new TreeNode (v);
    // 如果原来是左子树，重置后目标节点还是在左子树上，否则相反
    if (isLeft) {
      newNode.left = node;
    } else {
      newNode.right = node;
    }
    return newNode;
  }
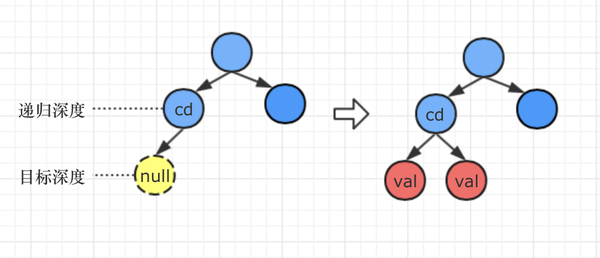
  // 处理上述的第1和第2种情况
  if (node.left || (node.left === null && cd + 1 === td)) {
    node.left = traversal (node.left, v, cd + 1, td, true);
  }
  if (node.right || (node.right === null && cd + 1 === td)) {
    node.right = traversal (node.right, v, cd + 1, td, false);
  }
  return node;
};
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} v
 * @param {number} d
 * @return {TreeNode}
 */
var addOneRow = function (root, v, td) {
  // 处理目标深度为1的情况，也就是上述的第3种情况
  if (td === 1) {
    const n = new TreeNode (v);
    n.left = root;
    return n;
  }
  traversal (root, v, 1, td);
  return root;
};

单词拆分

题目描述 

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

1.拆分时可以重复使用字典中的单词。

2.你可以假设字典中没有重复的单词。

Example 

example1
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
注意: 你可以重复使用字典中的单词。

example2
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/word-break

基本思想 

动态规划

具体分析

动态规划的关键点是：寻找状态转移方程

有了这个状态转移方程，我们就可以根据上一阶段状态和决策结果，去求出本阶段的状态和结果

然后，就可以从初始值，不断递推求出最终结果。

在这个问题里，我们使用一个一维数组来存放动态规划过程的递推数据

假设这个数组为dp，数组元素都为true或者false,

dp[N] 存放的是字符串s中从0到N截取的子串是否是“可拆分”的布尔值

让我们从一个具体的中间场景出发来思考计算过程

假设我们有

wordDict = ['ab','cd','ef']
s ='abcdef'

并且假设目前我们已经得出了N=1到N=5的情况，而现在需要计算N=6的情况

或者说，我们已经求出了dp[1] 到dp[5]的布尔值，现在需要计算dp[6] = ?

 

该怎么计算呢？

现在新的字符f被加入到序列“abcde”的后面，如此以来，就新增了以下几种6种需要计算的情况

A序列 + B序列
1.abcdef + ""
2.abcde + f
3.abcd + ef
4.abc + def
5.ab + cdef
6.a + bcdef
注意：当A可拆且B可拆时，则A+B也是可拆分的

从中我们不难发现两点

1. 当A可拆且B可拆时，则A+B也是可拆分的

2. 这6种情况只要有一种组合序列是可拆分的，abcdef就一定是可拆的，也就得出dp[6] = true了

下面是根据根据已有的dp[1] 到dp[5]的布尔值，动态计算dp[6] 的过程

（注意只要计算到可拆，就可以break循环了）

 

具体代码

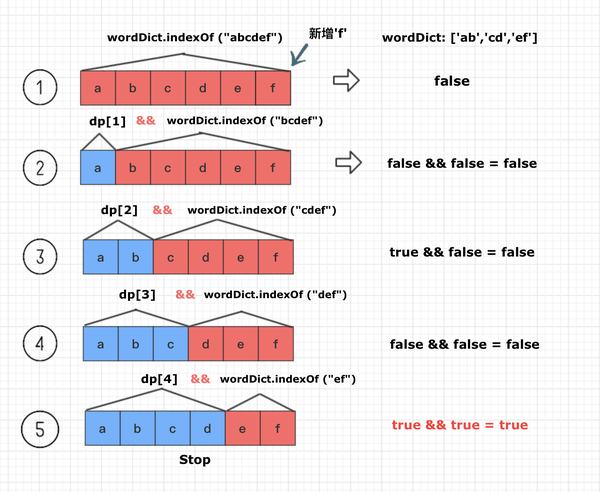
var initDp = function (len) {
  let dp = new Array (len + 1).fill (false);
  return dp;
};
/**
 * @param {string} s
 * @param {string[]} wordDict
 * @return {boolean}
 */
var wordBreak = function (s, wordDict) {
  // 处理空字符串
  if (s === '' && wordDict.indexOf ('') === -1) {
    return false;
  }
  const len = s.length;
  // 默认初始值全部为false
  const dp = initDp (len);
  const a = s.charAt (0);
  // 初始化动态规划的初始值
  dp[0] = wordDict.indexOf (a) === -1 ? false : true;
  dp[1] = wordDict.indexOf (a) === -1 ? false : true;
  // i:end
  // j:start
  for (let i = 1; i < len; i++) {
    for (let j = 0; j <= i; j++) {
      // 序列[0,i] = 序列[0,j] + 序列[j,i]
      // preCanBreak表示序列[0,j]是否是可拆分的
      const preCanBreak = dp[j];
      // 截取序列[j,i]
      const str = s.slice (j, i + 1);
      // curCanBreak表示序列[j,i]是否是可拆分的
      const curCanBreak = wordDict.indexOf (str) !== -1;
      // 情况1: 序列[0,j]和序列[j,i]都可拆分，那么序列[0,i]肯定也是可拆分的
      const flag1 = preCanBreak && curCanBreak;
      // 情况2: 序列[0,i]本身就存在于字典中，所以是可拆分的
      const flag2 = curCanBreak && j === 0;
      if (flag1 || flag2) {
        // 设置bool值，本轮计算结束
        dp[i + 1] = true;
        break;
      }
    }
  }
  // 返回最后结果
  return dp[len];
};

全排列

题目描述

给定一个没有重复数字的序列，返回其所有可能的全排列。

Example

输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/permutations

基本思想

回溯法

具体分析

1. 深度优先搜索搞一波，index在递归中向前推进

2. 当index等于数组长度的时候，结束递归，收集到results中（数组记得要深拷贝哦）

3. 两次数字交换的运用，计算出两种情况

总结

想不通没关系，套路一波就完事了

具体代码

var swap = function (nums, i, j) {
  const temp = nums[i];
  nums[i] = nums[j];
  nums[j] = temp;
};

var recursion = function (nums, results, index) {
  // 剪枝
  if (index >= nums.length) {
    results.push (nums.concat ());
    return;
  }
  // 初始化i为index
  for (let i = index; i < nums.length; i++) {
    // index 和 i交换？？
    // 统计交换和没交换的两种情况
    swap (nums, index, i);
    recursion (nums, results, index + 1);
    swap (nums, index, i);
  }
};
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function (nums) {
  const results = [];
  recursion (nums, results, 0);
  return results;
};