MATLAB实例:PCA降维
MATLAB实例:PCA降维
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
1. iris数据
5.1,3.5,1.4,0.2,1
4.9,3.0,1.4,0.2,1
4.7,3.2,1.3,0.2,1
4.6,3.1,1.5,0.2,1
5.0,3.6,1.4,0.2,1
5.4,3.9,1.7,0.4,1
4.6,3.4,1.4,0.3,1
5.0,3.4,1.5,0.2,1
4.4,2.9,1.4,0.2,1
4.9,3.1,1.5,0.1,1
5.4,3.7,1.5,0.2,1
4.8,3.4,1.6,0.2,1
4.8,3.0,1.4,0.1,1
4.3,3.0,1.1,0.1,1
5.8,4.0,1.2,0.2,1
5.7,4.4,1.5,0.4,1
5.4,3.9,1.3,0.4,1
5.1,3.5,1.4,0.3,1
5.7,3.8,1.7,0.3,1
5.1,3.8,1.5,0.3,1
5.4,3.4,1.7,0.2,1
5.1,3.7,1.5,0.4,1
4.6,3.6,1.0,0.2,1
5.1,3.3,1.7,0.5,1
4.8,3.4,1.9,0.2,1
5.0,3.0,1.6,0.2,1
5.0,3.4,1.6,0.4,1
5.2,3.5,1.5,0.2,1
5.2,3.4,1.4,0.2,1
4.7,3.2,1.6,0.2,1
4.8,3.1,1.6,0.2,1
5.4,3.4,1.5,0.4,1
5.2,4.1,1.5,0.1,1
5.5,4.2,1.4,0.2,1
4.9,3.1,1.5,0.1,1
5.0,3.2,1.2,0.2,1
5.5,3.5,1.3,0.2,1
4.9,3.1,1.5,0.1,1
4.4,3.0,1.3,0.2,1
5.1,3.4,1.5,0.2,1
5.0,3.5,1.3,0.3,1
4.5,2.3,1.3,0.3,1
4.4,3.2,1.3,0.2,1
5.0,3.5,1.6,0.6,1
5.1,3.8,1.9,0.4,1
4.8,3.0,1.4,0.3,1
5.1,3.8,1.6,0.2,1
4.6,3.2,1.4,0.2,1
5.3,3.7,1.5,0.2,1
5.0,3.3,1.4,0.2,1
7.0,3.2,4.7,1.4,2
6.4,3.2,4.5,1.5,2
6.9,3.1,4.9,1.5,2
5.5,2.3,4.0,1.3,2
6.5,2.8,4.6,1.5,2
5.7,2.8,4.5,1.3,2
6.3,3.3,4.7,1.6,2
4.9,2.4,3.3,1.0,2
6.6,2.9,4.6,1.3,2
5.2,2.7,3.9,1.4,2
5.0,2.0,3.5,1.0,2
5.9,3.0,4.2,1.5,2
6.0,2.2,4.0,1.0,2
6.1,2.9,4.7,1.4,2
5.6,2.9,3.6,1.3,2
6.7,3.1,4.4,1.4,2
5.6,3.0,4.5,1.5,2
5.8,2.7,4.1,1.0,2
6.2,2.2,4.5,1.5,2
5.6,2.5,3.9,1.1,2
5.9,3.2,4.8,1.8,2
6.1,2.8,4.0,1.3,2
6.3,2.5,4.9,1.5,2
6.1,2.8,4.7,1.2,2
6.4,2.9,4.3,1.3,2
6.6,3.0,4.4,1.4,2
6.8,2.8,4.8,1.4,2
6.7,3.0,5.0,1.7,2
6.0,2.9,4.5,1.5,2
5.7,2.6,3.5,1.0,2
5.5,2.4,3.8,1.1,2
5.5,2.4,3.7,1.0,2
5.8,2.7,3.9,1.2,2
6.0,2.7,5.1,1.6,2
5.4,3.0,4.5,1.5,2
6.0,3.4,4.5,1.6,2
6.7,3.1,4.7,1.5,2
6.3,2.3,4.4,1.3,2
5.6,3.0,4.1,1.3,2
5.5,2.5,4.0,1.3,2
5.5,2.6,4.4,1.2,2
6.1,3.0,4.6,1.4,2
5.8,2.6,4.0,1.2,2
5.0,2.3,3.3,1.0,2
5.6,2.7,4.2,1.3,2
5.7,3.0,4.2,1.2,2
5.7,2.9,4.2,1.3,2
6.2,2.9,4.3,1.3,2
5.1,2.5,3.0,1.1,2
5.7,2.8,4.1,1.3,2
6.3,3.3,6.0,2.5,3
5.8,2.7,5.1,1.9,3
7.1,3.0,5.9,2.1,3
6.3,2.9,5.6,1.8,3
6.5,3.0,5.8,2.2,3
7.6,3.0,6.6,2.1,3
4.9,2.5,4.5,1.7,3
7.3,2.9,6.3,1.8,3
6.7,2.5,5.8,1.8,3
7.2,3.6,6.1,2.5,3
6.5,3.2,5.1,2.0,3
6.4,2.7,5.3,1.9,3
6.8,3.0,5.5,2.1,3
5.7,2.5,5.0,2.0,3
5.8,2.8,5.1,2.4,3
6.4,3.2,5.3,2.3,3
6.5,3.0,5.5,1.8,3
7.7,3.8,6.7,2.2,3
7.7,2.6,6.9,2.3,3
6.0,2.2,5.0,1.5,3
6.9,3.2,5.7,2.3,3
5.6,2.8,4.9,2.0,3
7.7,2.8,6.7,2.0,3
6.3,2.7,4.9,1.8,3
6.7,3.3,5.7,2.1,3
7.2,3.2,6.0,1.8,3
6.2,2.8,4.8,1.8,3
6.1,3.0,4.9,1.8,3
6.4,2.8,5.6,2.1,3
7.2,3.0,5.8,1.6,3
7.4,2.8,6.1,1.9,3
7.9,3.8,6.4,2.0,3
6.4,2.8,5.6,2.2,3
6.3,2.8,5.1,1.5,3
6.1,2.6,5.6,1.4,3
7.7,3.0,6.1,2.3,3
6.3,3.4,5.6,2.4,3
6.4,3.1,5.5,1.8,3
6.0,3.0,4.8,1.8,3
6.9,3.1,5.4,2.1,3
6.7,3.1,5.6,2.4,3
6.9,3.1,5.1,2.3,3
5.8,2.7,5.1,1.9,3
6.8,3.2,5.9,2.3,3
6.7,3.3,5.7,2.5,3
6.7,3.0,5.2,2.3,3
6.3,2.5,5.0,1.9,3
6.5,3.0,5.2,2.0,3
6.2,3.4,5.4,2.3,3
5.9,3.0,5.1,1.8,3
2. MATLAB程序
function [COEFF,SCORE,latent,tsquared,explained,mu,data_PCA]=pca_demo()
x=load('iris.data');
[~,d]=size(x);
k=d-1; %前k个主成分
x=zscore(x(:,1:d-1)); %归一化数据
[COEFF,SCORE,latent,tsquared,explained,mu]=pca(x);
% 1)获取样本数据 X ,样本为行,特征为列。
% 2)对样本数据中心化,得S(S = X的各列减去各列的均值)。
% 3)求 S 的协方差矩阵 C = cov(S)
% 4) 对协方差矩阵 C 进行特征分解 [P,Lambda] = eig(C);
% 5)结束。
% 1、输入参数 X 是一个 n 行 p 列的矩阵。每行代表一个样本观察数据,每列则代表一个属性,或特征。
% 2、COEFF 就是所需要的特征向量组成的矩阵,是一个 p 行 p 列的矩阵,没列表示一个出成分向量,经常也称为(协方差矩阵的)特征向量。并且是按照对应特征值降序排列的。所以,如果只需要前 k 个主成分向量,可通过:COEFF(:,1:k) 来获得。
% 3、SCORE 表示原数据在各主成分向量上的投影。但注意:是原数据经过中心化后在主成分向量上的投影。即通过:SCORE = x0*COEFF 求得。其中 x0 是中心平移后的 X(注意:是对维度进行中心平移,而非样本。),因此在重建时,就需要加上这个平均值了。
% 4、latent 是一个列向量,表示特征值,并且按降序排列。
% 5、tsquared Hotelling的每个观测值X的T平方统计量
% 6、explained 由每个主成分解释的总方差的百分比
% 7、mu 每个变量X的估计平均值
% x= bsxfun(@minus,x,mean(x,1));
data_PCA=x*COEFF(:,1:k);
latent1=100*latent/sum(latent);%将latent总和统一为100,便于观察贡献率
pareto(latent1);%调用matla画图 pareto仅绘制累积分布的前95%,因此y中的部分元素并未显示
xlabel('Principal Component');
ylabel('Variance Explained (%)');
% 图中的线表示的累积变量解释程度
print(gcf,'-dpng','Iris PCA.png');
iris_pac=data_PCA(:,1:2) ;
save iris_pca iris_pac
3. 结果
iris_pca:前两个主成分
-2.25698063306803 0.504015404227653
-2.07945911889541 -0.653216393612590
-2.36004408158421 -0.317413944570283
-2.29650366000389 -0.573446612971233
-2.38080158645275 0.672514410791076
-2.06362347633724 1.51347826673567
-2.43754533573242 0.0743137171331950
-2.22638326740708 0.246787171742162
-2.33413809644009 -1.09148977019584
-2.18136796941948 -0.447131117450110
-2.15626287481026 1.06702095645556
-2.31960685513084 0.158057945820095
-2.21665671559727 -0.706750478104682
-2.63090249246321 -0.935149145374822
-2.18497164997156 1.88366804891533
-2.24394778052703 2.71328133141014
-2.19539570001472 1.50869601039751
-2.18286635818774 0.512587093716441
-1.88775015418968 1.42633236069007
-2.33213619695782 1.15416686250116
-1.90816386828207 0.429027879924458
-2.19728429051438 0.949277150423224
-2.76490709741649 0.487882574439700
-1.81433337754274 0.106394361814184
-2.22077768737273 0.161644638073716
-1.95048968523510 -0.605862870440206
-2.04521166172712 0.265126114804279
-2.16095425532709 0.550173363315497
-2.13315967968331 0.335516397664229
-2.26121491382610 -0.313827252316662
-2.13739396044139 -0.482326258880086
-1.82582143036022 0.443780130732953
-2.59949431958629 1.82237008322707
-2.42981076672382 2.17809479520796
-2.18136796941948 -0.447131117450110
-2.20373717203888 -0.183722323644913
-2.03759040170113 0.682669420156327
-2.18136796941948 -0.447131117450110
-2.42781878392261 -0.879223932713649
-2.16329994558551 0.291749566745466
-2.27889273592867 0.466429134628597
-1.86545776627869 -2.31991965918865
-2.54929404704891 -0.452301129580194
-1.95772074352968 0.495730895348582
-2.12624969840005 1.16752080832811
-2.06842816583668 -0.689607099127106
-2.37330741591874 1.14679073709691
-2.39018434748641 -0.361180775489047
-2.21934619663183 1.02205856145225
-2.19858869176329 0.0321302060908945
1.10030752013391 0.860230593245533
0.730035752246062 0.596636784545418
1.23796221659453 0.612769614333371
0.395980710562889 -1.75229858398514
1.06901265623960 -0.211050862633647
0.383174475987114 -0.589088965722193
0.746215185580377 0.776098608766709
-0.496201068006129 -1.84269556949638
0.923129796737431 0.0302295549588077
0.00495143780650871 -1.02596403732389
-0.124281108093219 -2.64918765259090
0.437265238506424 -0.0586846858581760
0.549792126592992 -1.76666307900171
0.714770518429262 -0.184815166484382
-0.0371339806719297 -0.431350035919633
0.872966018474250 0.508295314415273
0.346844440799832 -0.189985178614466
0.152880381053472 -0.788085297090142
1.21124542423444 -1.62790202112846
0.156417163578196 -1.29875232891050
0.735791135537219 0.401126570248885
0.470792483676532 -0.415217206131680
1.22388807504403 -0.937773165086814
0.627279600231826 -0.415419947028686
0.698133985336190 -0.0632819273014206
0.870620328215835 0.249871517845242
1.25003445866275 -0.0823442389434431
1.35370481019450 0.327722365822153
0.659915359649250 -0.223597000167979
-0.0471236447211597 -1.05368247816741
0.121128417400412 -1.55837168956507
0.0140710866007487 -1.56813894313840
0.235222818975321 -0.773333046281646
1.05316323317206 -0.634774729305402
0.220677797156699 -0.279909968621073
0.430341476713787 0.852281697154445
1.04590946111265 0.520453696157683
1.03241950881290 -1.38781716762055
0.0668436673617666 -0.211910813930204
0.274505447436587 -1.32537578085168
0.271425764670620 -1.11570381243558
0.621089830946741 0.0274506709978046
0.328903506457842 -0.985598883763833
-0.372380114621411 -2.01119457605980
0.281999617970590 -0.851099454545845
0.0887557702224096 -0.174324544331148
0.223607676665854 -0.379214256409087
0.571967341693057 -0.153206717308028
-0.455486948803962 -1.53432438068788
0.251402252309636 -0.593871222060355
1.84150338645482 0.868786147264828
1.14933941416981 -0.698984450845645
2.19898270027627 0.552618780551384
1.43388176486790 -0.0498435417617587
1.86165398830779 0.290220535935809
2.74500070081969 0.785799704159685
0.357177895625210 -1.55488557249365
2.29531637451915 0.408149356863061
1.99505169024551 -0.721448439846371
2.25998344407884 1.91502747107928
1.36134878398531 0.691631011499905
1.59372545693795 -0.426818952656741
1.87796051113409 0.412949339203311
1.24890257443547 -1.16349352357816
1.45917315700813 -0.442664601834978
1.58649439864337 0.674774813132046
1.46636772102851 0.252347085727036
2.42924030093571 2.54822056527013
3.29809226641255 -0.00235343587272177
1.24979406018816 -1.71184899071237
2.03368323142868 0.904369044486726
0.970663302005081 -0.569267277965818
2.88838806680663 0.396463170625287
1.32475563655861 -0.485135293486995
1.69855040646181 1.01076227706927
1.95119099025002 0.999984474306318
1.16799162725452 -0.317831851008113
1.01637609822602 0.0653241212065782
1.78004554289349 -0.192627479858818
1.85855159177699 0.553527164026207
2.42736549094542 0.245830911619345
2.30834922706014 2.61741528404554
1.85415981777379 -0.184055790370030
1.10756129219332 -0.294997832217552
1.19347091639304 -0.814439294423699
2.79159729280499 0.841927657717863
1.57487925633390 1.06889360300461
1.34254676764379 0.420846092290459
0.920349720485088 0.0191661621187343
1.84736314547313 0.670177571688802
2.00942543830962 0.608358978317639
1.89676252747561 0.683734258412757
1.14933941416981 -0.698984450845645
2.03648602144585 0.861797777652503
1.99500750598298 1.04504903502442
1.86427657131500 0.381543630923962
1.55328823048458 -0.902290843047121
1.51576710303099 0.265903772450991
1.37179554779330 1.01296839034343
0.956095566421630 -0.0222095406309480
累计贡献率
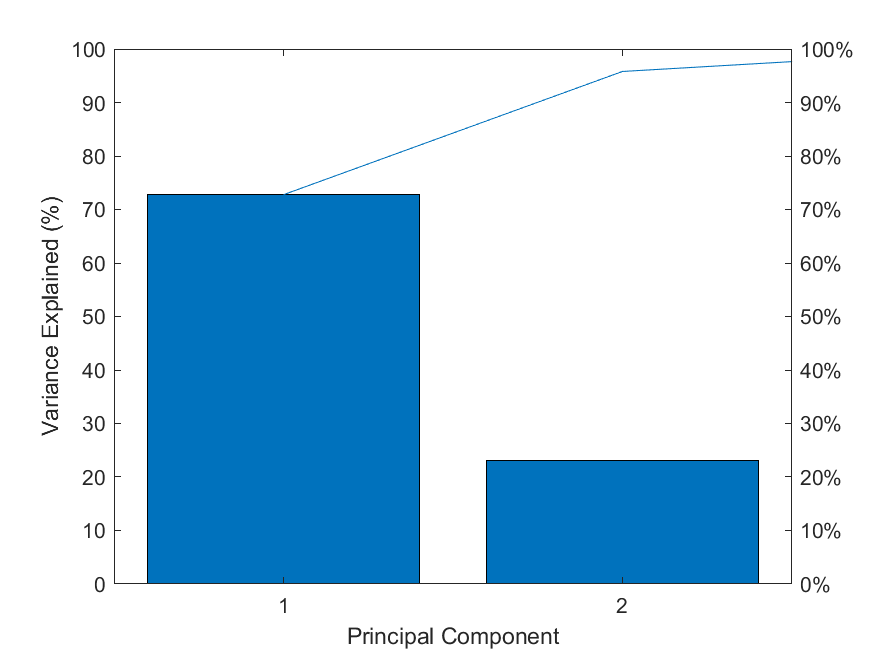
可见:前两个主成分已经占了95%的贡献程度。这两个主成分可以近似表示整个数据。
4. pca_data.m
其中normlization.m见MATLAB实例:聚类初始化方法与数据归一化方法
function data=pca_data(data, choose)
% PCA降维,保留90%的特征信息
data = normlization(data, choose); %归一化
score = 0.90; %保留90%的特征信息
[num,dim] = size(data);
xbar = mean(data,1);
means = bsxfun(@minus, data, xbar);
cov = means'*means/num;
[V,D] = eig(cov);
eigval = diag(D);
[~,idx] = sort(eigval,'descend');
eigval = eigval(idx);
V = V(idx,:);
p = 0;
for i=1:dim
perc = sum(eigval(1:i))/sum(eigval);
if perc > score
p = i;
break;
end
end
E = V(1:p,:);
data= means*E';
参考:
Junhao Hua. Distributed Variational Bayesian Algorithms. Github, 2017.
MATLAB实例:PCA降维的更多相关文章
- MATLAB实例:PCA(主成成分分析)详解
MATLAB实例:PCA(主成成分分析)详解 作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 1. 主成成分分析 2. MATLAB解释 详细信息请看: ...
- PCA降维2
前言 本文为模式识别系列第一篇,主要介绍主成分分析算法(Principal Component Analysis,PCA)的理论,并附上相关代码.全文主要分六个部分展开: 1)简单示例.通过简单的例子 ...
- [综] PCA降维
http://blog.json.tw/using-matlab-implementing-pca-dimension-reduction 設有m筆資料, 每筆資料皆為n維, 如此可將他們視為一個mx ...
- 机器学习公开课笔记(8):k-means聚类和PCA降维
K-Means算法 非监督式学习对一组无标签的数据试图发现其内在的结构,主要用途包括: 市场划分(Market Segmentation) 社交网络分析(Social Network Analysis ...
- Python机器学习笔记 使用scikit-learn工具进行PCA降维
之前总结过关于PCA的知识:深入学习主成分分析(PCA)算法原理.这里打算再写一篇笔记,总结一下如何使用scikit-learn工具来进行PCA降维. 在数据处理中,经常会遇到特征维度比样本数量多得多 ...
- PCA降维—降维后样本维度大小
之前对PCA的原理挺熟悉,但一直没有真正使用过.最近在做降维,实际用到了PCA方法对样本特征进行降维,但在实践过程中遇到了降维后样本维数大小限制问题. MATLAB自带PCA函数:[coeff, sc ...
- 一步步教你轻松学主成分分析PCA降维算法
一步步教你轻松学主成分分析PCA降维算法 (白宁超 2018年10月22日10:14:18) 摘要:主成分分析(英语:Principal components analysis,PCA)是一种分析.简 ...
- PCA 降维算法详解 以及代码示例
转载地址:http://blog.csdn.net/watkinsong/article/details/38536463 1. 前言 PCA : principal component analys ...
- PCA降维技术
PCA降维技术 PCA 降维 Fly Time: 2017-2-28 主成分分析(PCA) PCA Algorithm 实例 主成分分析(PCA) 主成分分析(Principal Component ...
随机推荐
- 转战物联网·基础篇05-通俗理解MQTT协议的实现原理和异步方式
网络上搜索MQTT协议,会出现太多的解释,这里就不做官方标准释义的复制了.这一节我们从实战理解角度,通俗的将MQTT协议的作用及实现原理说一下,旨在可以快速理解MQTT协议.所以可能会出现很多看似 ...
- Violet音乐社区需求分析说明书
目录 一.引言 1.1 编写目的 1.2 开发背景 1.3 开发工具 二.项目需求 2.1 角色定义 2.2 模块划分 2.3 功能概述 2.4 数据流图 三.前端页面 四.软件要求 4.1 性能要求 ...
- Linux:DNS服务器搭建
DNS简介 DNS(Domain Name System)域名系统: 是一种采用客户端/服务器机制,负责实现计算机名称与IP地址转换的系统.DNS作为一种重要的网络服务,既是国际互联网工作的基础,同时 ...
- 文件操作NIO
在丑陋的 Java I/O 编程方式诞生多年以后,Java终于简化了文件读写的基本操作. 两个基本组件 文件或者目录的路径: 文件本身. 这块基本都是些记忆性的东西,没什么过多的需要写的地方,用的时候 ...
- qt用于图片显示的窗口
用于图片显示的窗口 国产化
- RabbitMQ学习笔记(七、RabbitMQ实战)
目录: 削峰 分布式事务 削峰: 利用RabbitMQ队列消费特性避免峰值下的DB访问,缓解连接压力,在DB释放连接后再去消息数据. 分布式事务: )XA协议:它是一个分布式事务协议,由事务管理器和资 ...
- flask之请求与响应、闪现(阅后即焚)、请求扩展(before,after)、中间件、LOCAL对象、偏函数、
目录 1.flask请求与响应 2.闪现 3.请求扩展 4.中间件 5.LOCAL对象 6.偏函数 templates 1.flask请求与响应 from flask import Flask,req ...
- pytest执行用例时从conftest.py抛出ModuleNotFoundError:No module named 'XXX'异常的解决办法
一.问题描述 在项目根目录下执行整个测试用例,直接从conftest.py模块中抛出了ModuleNotFoundError:No module named 'TestDatas'的异常: 二.解决方 ...
- Jenkins登录后空白页
进入.jenkins所在的目录 编辑config.xml文件 重启jenkins
- 资源推荐:PPT快闪资源合集附配套字体下载
样例ppt下载 搜索公众号“拒收”或扫码关注公众号 回复关键字“快闪ppt”获取全部福利 本公众号只出精品,拒收劣质 或者点击菜单链接获取获取全部资源
