UVA 690 Pipeline Scheduling

https://vjudge.net/problem/UVA-690

题目

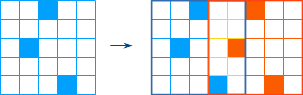
你有一台包含5个工作单元的计算机，还有10个完全相同的程序需要执行。每个程序需要$n(n<20)$个时间片来执行，可以用一个5行n列的保留表（reservation table）来表示，其中每行代表一个工作单元（unit0~unit4），每列代表一个时间片，行i列j的字符为X表示“在程序执行的第j个时间片中需要工作单元i”。例如，如图所示就是一张保留表，其中程序在执行的第0,1,2，……个时间片中分别需要unit0，unit1，unit2……

同一个工作单元不能同时执行多个程序，因此若两个程序分别从时间片0和1开始执行，则在时间片5时会发生冲突（两个程序都想使用unit0），如图所示。

输入一个5行n（n<20）列的保留表，输出所有10个程序执行完毕所需的最少时间，例如，对于图中的保留表，执行完10个程序最少需要34个时间片。

clock	0	1	2	3	4	5	6		clock	0	1	2	3	4	5	6	7
unit0	X	.	.	.	X	X	.		unit0	0	1	.	.	0	C	1	.
unit1	.	X	.	.	.	.	.		unit1	.	0	1	.	.	.	.	.
unit2	.	.	X	.	.	.	.		unit2	.	.	0	1	.	.	.	.
unit3	.	.	.	X	.	.	.		unit3	.	.	.	0	1	.	.	.
unit4	.	.	.	.	.	.	X		unit4	.	.	.	.	.	.	0	1

题解

我是真的服了这题了……还有昨天每次评测都要排半小时的队……

1.直接模拟，加上剪枝：如果剩余的程序全部使用最短移动仍然超过了当前最短的时间，那么就剪枝。提前计算移动的步数。但是这个方法容易TLE……

2.使用二进制压缩状态，加上剪枝

每次移动只需要判断原来的状态向后移与程序的保留表是否有冲突，如果没有，将这两个取并作为新的状态。

AC代码

#include<bits/stdc++.h>
using namespace std;
#define REP(r,x,y) for(register int r=(x); r<(y); r++)
#define REPE(r,x,y) for(register int r=(x); r<=(y); r++)
#define MAXN 17
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...)
#endif
int n;
int maxd;

int ans;
int tmp[5];
int can[450],cani=0;
void dfs(int d, int x, int pos, const int* lp) {
	if(pos+(9-d)*can[0]+n>=ans) { return;}
	REP(i,0,5)  {
		if(tmp[i] & (lp[i]>>x)) return;
	}
	int np[5]; memcpy(np,lp,sizeof np);

	REP(i,0,5) {
		np[i] = tmp[i] | (np[i]>>x);
	}

	if(d==9) {
//		assert(false);
		ans = min(ans,pos+n);
	} else {
		REP(i,0,cani) {
			dfs(d+1,can[i], pos+can[i],np);
		}
	}

}
int main() {
	#ifdef sahdsg
	freopen("in.txt", "r", stdin);
	#endif
	while(~scanf("%d", &n) && n) {
//		memset(vis,0,sizeof vis);
//		memset(pic,0,sizeof pic);
		maxd=-1;
		cani=0;
		memset(tmp,0,sizeof tmp);
		REP(i,0,5) REP(j,0,n) {
			char ch=getchar();
			while(ch<' ') ch=getchar();
			if(ch=='X') {
//				pic[i][j]=1;
				maxd=max(maxd,j);
				tmp[i]|=1<<j;
			}
		}
		REPE(d,1,maxd+1) {
			REP(i,0,5){
				if(tmp[i] & (tmp[i]>>d)) goto nxt;
			}
			can[cani++]=d;
			nxt:;
		}
		if(maxd==-1) assert(false);
		else {
			ans=9*(maxd+1)+n;
			REP(i,0,cani) {
				dfs(1,can[i], can[i],tmp);
			}
		}
		printf("%d\n", ans);
	}
	return 0;
}