A Simple Chess---hdu5794（容斥+Lucas）

题目链接：http://acm.split.hdu.edu.cn/showproblem.php?pid=5794

题意：给你一个n*m的网格，问从(1, 1)走到(n, m)的方案数是多少，其中有r个点是不可到达的；

根据公式我们可以知道每次只能走”日"型；

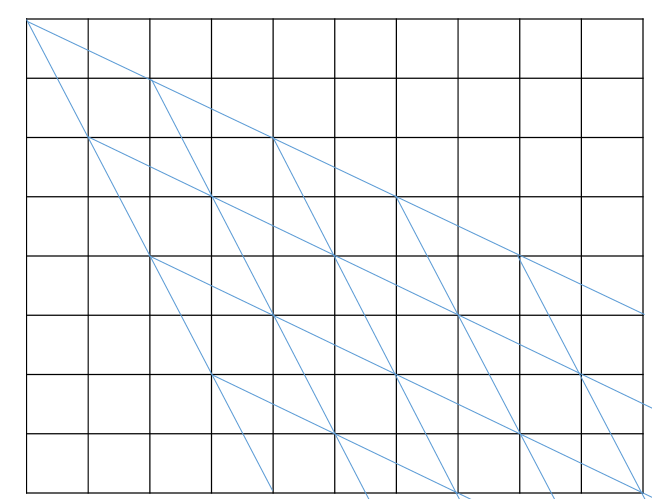
路径如上图所示，我们可以看到有很多点是不可达的,可达点都是满足(x+y)%3=2的;路径可以看成一个斜着放置的杨辉三角。我们只需要把坐标转换一下即可，这是没有障碍时的方案数；

让(1,1)到(n,m)中如果有一个障碍，那么我们可以用起点到终点的方法数-起点到障碍点的方法数*障碍点到终点的方法数；同样如果有 r 个，那就减去r次这样的情况；

同样处理到达每个点的时候也是这样处理的；

注意有不可达的，所以判断一下不然会re的；

#include<iostream>
#include<algorithm>
#include<string.h>
#include<stdio.h>
#include<math.h>
using namespace std;
#define N 120000
#define PI 4*atan(1.0)
#define mod 110119
#define met(a, b) memset(a, b, sizeof(a))
typedef long long LL;

struct node
{
    LL x, y;
    friend bool operator < (node p, node q)
    {
        if(p.x!=q.x)
            return p.x < q.x;
        return p.y < q.y;
    }
}a[];

LL f[N] = {};

LL Pow(LL a, LL b)
{
    LL ans = ;
    while(b)
    {
        if(b&)
            ans = ans*a%mod;
        b/=;
        a = a*a%mod;
    }
    return ans%mod;
}

LL C(LL n, LL m)
{
    if(m>n)return ;
    if(m == )return ;
    LL ans = f[n] * Pow(f[m], mod-)%mod * Pow(f[n-m], mod-) % mod;
    return ans;
}
LL Lucas(LL n, LL m)
{
    if(n< || m<)return ;///会出现不可达的情况，所以注意判断，否则会re；
    if(m > n) return ;
    if(m == ) return ;
    return C(n%mod, m%mod) * Lucas(n/mod, m/mod) % mod;
}

LL solve(LL x1, LL y1, LL x2, LL y2)
{
    if((x1+y1)% != )return ;
    if((x2+y2)% != )return ;

    LL ax = (x1+y1-)/;
    LL ay = y1 -  - ax;

    LL bx = (x2+y2-)/;
    LL by = y2 -  - bx;

    return Lucas(bx-ax, by-ay);
}

int main()
{
    for(int i=; i<=; i++)
        f[i] = f[i-]*i % mod;

    LL n, m;
    int t = , r;
    while(scanf("%I64d %I64d %d", &n, &m, &r)!=EOF)
    {
        LL ans[N];///起点到i的方案数；

        for(int i=; i<=r; i++)
            scanf("%I64d %I64d", &a[i].x, &a[i].y);

        sort(a+, a+r+);///按x的升序排列，再按y的升序排列；

        LL sum = solve(, , n, m);

        for(int i=; i<=r; i++)
        {
            ans[i] = solve(, , a[i].x, a[i].y);
            for(int j=; j<i; j++)
            {
                ans[i] = ((ans[i] - ans[j]*solve(a[j].x, a[j].y, a[i].x, a[i].y)%mod) + mod) % mod;
            }
        }
        for(int i=; i<=r; i++)
        {
            sum = (sum - ans[i]*solve(a[i].x, a[i].y, n, m)%mod + mod) % mod;
        }
        printf("Case #%d: %I64d\n", t++, sum);
    }
    return ;
}