深度遍历DFS

目录：

https://zhipianxuan.github.io/

一、树的DFS

二、二维矩阵的DFS

三、图的DFS

　　

一、题目一：二维矩阵（输出所有路径数）

思路：从起点开始，DFS，直到走到终点，用一个全局变量res[0]记录所有路径数量。

　代码：

#row, col = map(int, input().split())

#graph = []
#for _ in range(row):
   # graph.append(list(map(int, input().split())))
#print(graph)

#x1, y1, x2, y2 = map(int, input().split())

dirs = [(-1, 0), (1, 0), (0, 1), (0, -1)]
M = 10 ** 9
res = [0]

graph = [[0, 1, 0, 0, 0], [0, 2, 3, 0, 0], [0, 0, 4, 5, 0], [0, 0, 7, 6, 0]]
row = 4
col = 5
x1, y1, x2, y2 = 0, 1, 3, 2

def dfs(x1, y1, visited):
    if x1 == x2 and y1 == y2:
        res[0] += 1
        return
    for i, j in dirs:
        tmp_x = i + x1
        tmp_y = j + y1
        if 0 <= tmp_x < row and 0 <= tmp_y < col and graph[tmp_x][tmp_y] > graph[x1][y1] \
                and (tmp_x, tmp_y) not in visited:
            dfs(tmp_x, tmp_y, visited | {(tmp_x, tmp_y)})

dfs(x1, y1, {(x1, y1)})
print(res[0] % M)

二、题目：岛屿的最大面积

给定一个包含了一些 0 和 1的非空二维数组 grid , 一个 岛屿 是由四个方向 (水平或垂直) 的 1 (代表土地) 构成的组合。你可以假设二维矩阵的四个边缘都被水包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为0。)

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是11，因为岛屿只能包含水平或垂直的四个方向的‘1’。

示例 2:

[[0,0,0,0,0,0,0,0]]

对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

思路：【来自LeetCode别人的解法】

遍历矩阵，遇到 grid [i] [j] = 1时，就算值【采用dfs来算】

dfs : 先将grid [i] [j] 置0，然后再 return 1 + dfs [i-1] [j] + dfs [i+1] [j] +dfs [i] [j-1] +dfs [i] [j+1]

　代码：

　　

 def maxAreaOfIsland(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        if not grid:
            return 0
        l,h = len(grid),len(grid[0])

        def dfs(i,j):
            if 0 <= i < l and 0 <= j < h and grid[i][j]:
                grid[i][j] = 0
                return 1 + dfs(i-1,j) + dfs(i+1,j) +dfs(i,j-1) + dfs(i,j+1)
            return 0

        result = [dfs(i,j) for i in range(l) for j in range(h) if grid[i][j]]
        return max(result) if result else 0

三、题目：最大正方形

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

示例:

输入:

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

输出: 4

思路：

代码：

public class Solution {
    public int maximalSquare(char[][] matrix) {
        if(matrix.length == 0) return 0;
        int m = matrix.length, n = matrix[0].length;
        int max = 0;
        int[][] dp = new int[m][n];
        // 第一列赋值
        for(int i = 0; i < m; i++){
            dp[i][0] = matrix[i][0] - '';
            max = Math.max(max, dp[i][0]);
        }
        // 第一行赋值
        for(int i = 0; i < n; i++){
            dp[0][i] = matrix[0][i] - '';
            max = Math.max(max, dp[0][i]);
        }
        // 递推
        for(int i = 1; i < m; i++){
            for(int j = 1; j < n; j++){
                dp[i][j] = matrix[i][j] == '' ? Math.min(dp[i-1][j-1], Math.min(dp[i-1][j], dp[i][j-1])) + 1 : 0;
                max = Math.max(max, dp[i][j]);
            }
        }
        return max * max;
    }
}

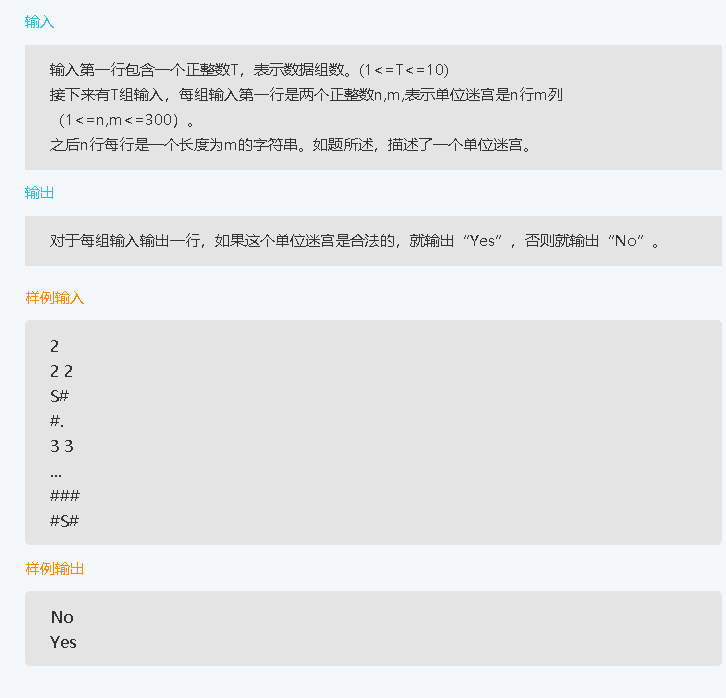
四、京东2019算法笔试题