Linear System

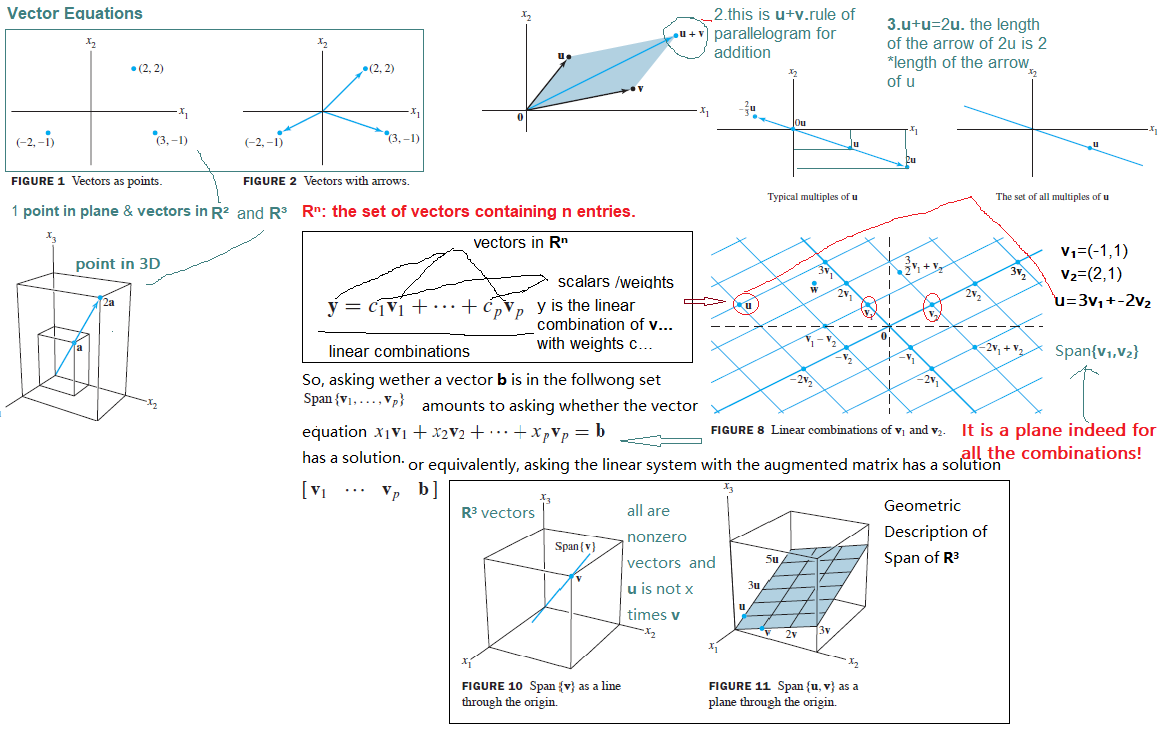
Vector Equations

The Matrix Equation

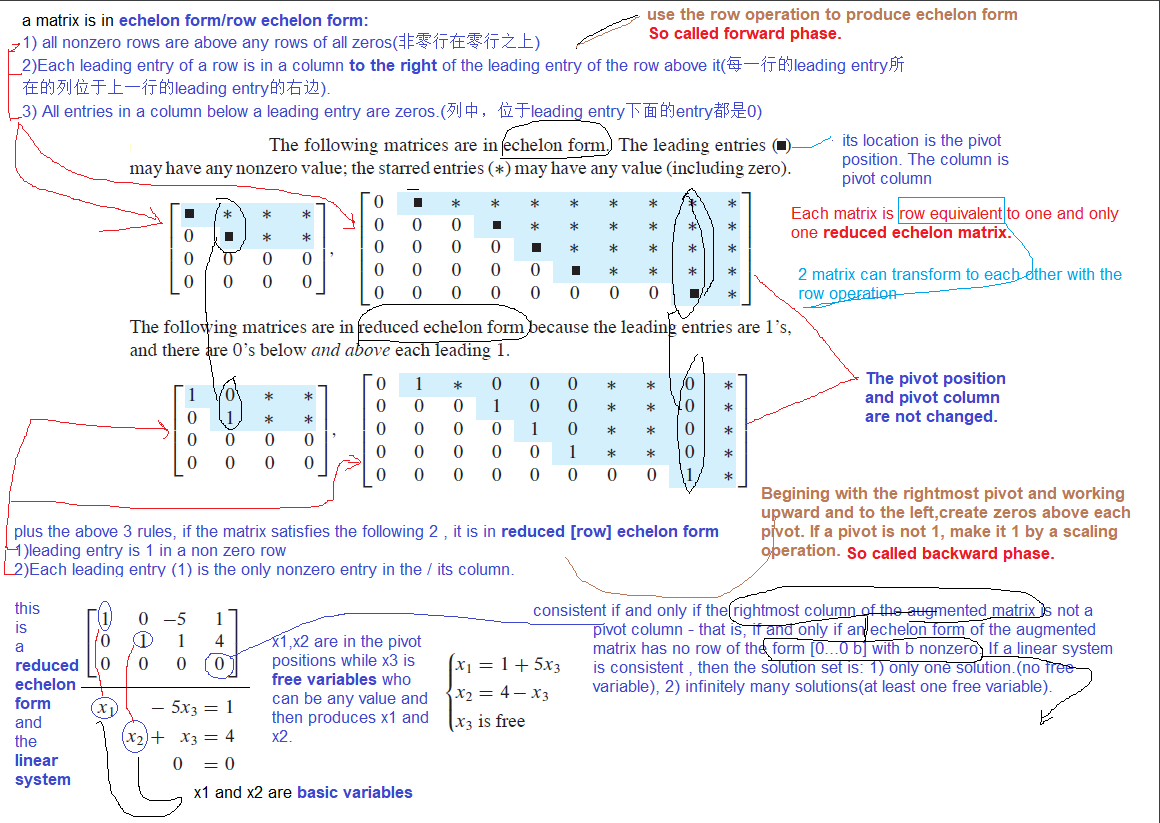
Solution Sets of Linear Systems

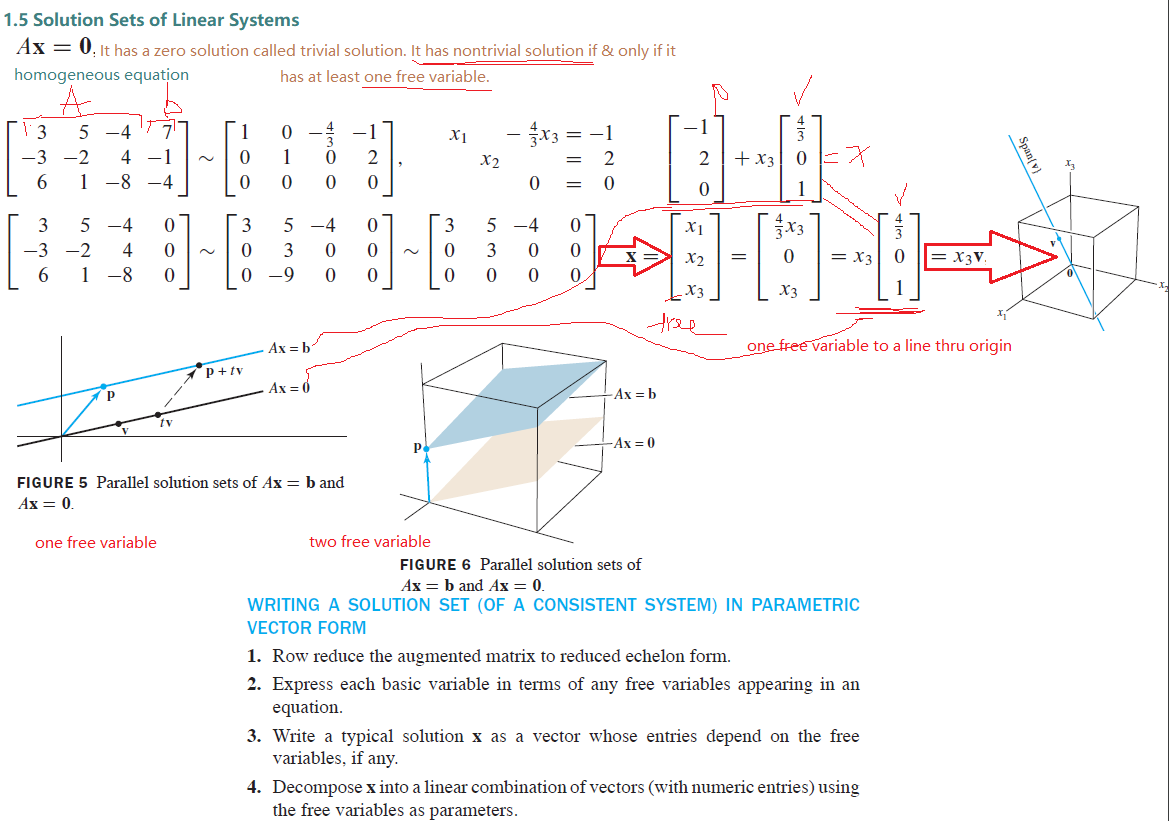
Linear Indenpendent

Introduction to Linear Transformation

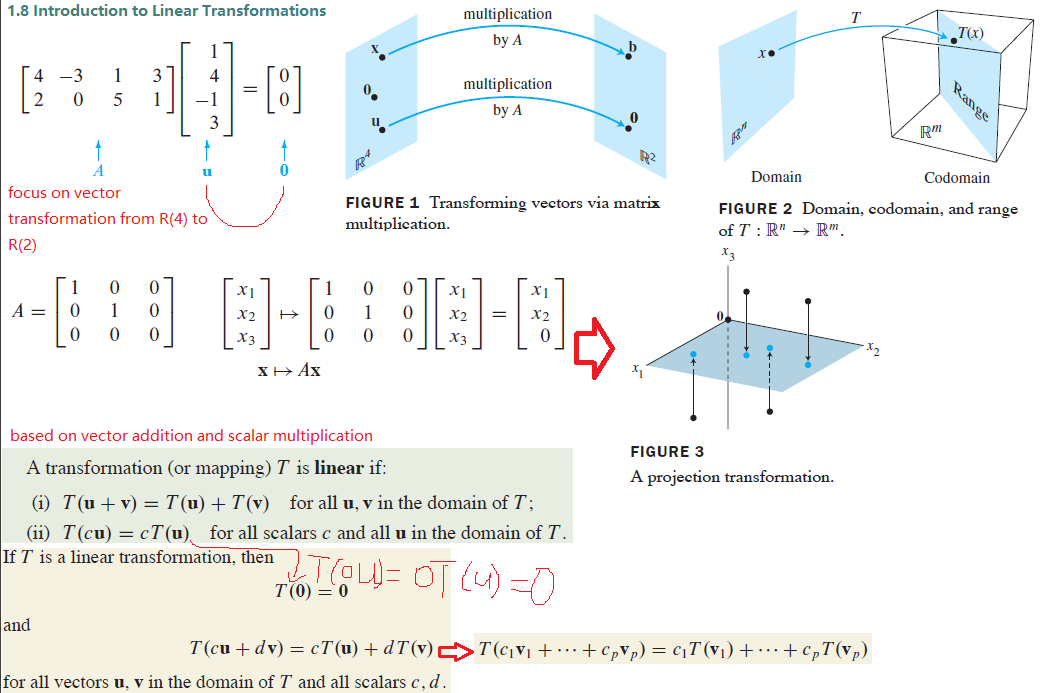
The Matrix of Linear Transformation

The Matrix of a Linear Transformation

Linear Equations in Linear Algebra的更多相关文章

  1. Linear Equations

    4.1 Linear Equations with One Independent Variable

  2. [Scikit-learn] 1.1 Generalized Linear Models - from Linear Regression to L1&L2

    Introduction 一.Scikit-learning 广义线性模型 From: http://sklearn.lzjqsdd.com/modules/linear_model.html#ord ...

  3. 个案排秩 Rank (linear algebra) 秩 (线性代数)

    非叫“秩”不可,有秩才有解_王治祥_新浪博客http://blog.sina.com.cn/s/blog_8e7bc4f801012c23.html 我在一个大学当督导的时候,一次我听一位老师给学生讲 ...

  4. 【读书笔记】：MIT线性代数(1):Linear Combinations

    1. Linear Combination Two linear operations of vectors: Linear combination: 2.Geometric Explaination ...

  5. [线性代数] 线性代数入门A Gentle Introduction

    An Overview: System of Linear Equations Basically, linear algebra solves system of linear equations ...

  6. 线性代数导论 | Linear Algebra 课程

    搞统计的线性代数和概率论必须精通,最好要能锻炼出直觉,再学机器学习才会事半功倍. 线性代数只推荐Prof. Gilbert Strang的MIT课程,有视频,有教材,有习题,有考试,一套学下来基本就入 ...

  7. 机器学习笔记1——Linear Regression with One Variable

    Linear Regression with One Variable Model Representation Recall that in *regression problems*, we ar ...

  8. 【转】Derivation of the Normal Equation for linear regression

    I was going through the Coursera "Machine Learning" course, and in the section on multivar ...

  9. 【线性代数】7-1:线性变换思想(The Idea of a Linear Transformation)

    title: [线性代数]7-1:线性变换思想(The Idea of a Linear Transformation) categories: Mathematic Linear Algebra k ...

随机推荐

  1. C++练习 | 创建并正序输出不带头结点的链表

    #include <iostream> #include <cstdio> #include <stdlib.h> using namespace std; str ...

  2. 实现一个shell程序

    实现一个自己的shell程序,这个程序有这些功能:解释执行命令,支持输入输出重定向,支持管道,后台运行 程序.当运行该程序后,它支持以下的命令格式: 1.单个命令,如:ls.2.带l到多个参数的命令, ...

  3. ATM购物作业

    一. 基本需求 模拟实现一个ATM + 购物商城程序 额度 15000或自定义 实现购物商城,买东西加入 购物车,调用信用卡接口结账 可以提现,手续费5% 支持多账户登录 支持账户间转账 记录日常消费 ...

  4. 对布局定位设置-position

    使用position属性,会激活5个属性 left right bottom top z-index(-1至999) 注:z-index:会改变内容的层级关系, 1.绝对定位 position: ab ...

  5. react-router-dom实现全局路由登陆拦截

    相比与vue的路由集中式管理,能够很好的进行统一的路由操作,react的路由看起来更乱,想要进行像vue的全局路由管理不是那么得心应手.在我们的项目中,有很多页面是需要登陆权限验证的,最好的方式就是能 ...

  6. Mac下PHP的环境搭建

    * 前段时间手欠 ... 入手了一个二手的Macbook pro ! 配置挺高的 16款13寸的基本顶配了 ... 只差 硬盘不是1T的 ... 可以脑补一下配置了* 话说 不是所有程序猿都说 每个程 ...

  7. php ecshop 二级域名切换跳转时session不同步，解决session无法共享同步导致无法登陆或者无法退出的问题

    echshop基础上做了单点登录的 一级域名与二级域名 退出时 清空session 都是一级域名的session 因为二级域名的session是设置在二级域名上的 echshop基础上没有做单点登录的 ...

  8. 基于C语言的面向对象编程

    嵌入式软件开发中,虽然很多的开发工具已经支持C++的开发,但是因为有时考虑运行效率和编程习惯,还是有很多人喜欢用C来开发嵌入式软件.Miro Samek说:"我在开发现场发现,很多嵌入式软件 ...

  9. DMVPN的实验模拟与分析

    此篇博客正在介绍的是下图中的DMVPN: 为什么会出现DMVPN这个技术呢? 在这篇博客中https://www.cnblogs.com/huwentao/p/9355240.html介绍过Dynam ...

  10. docker-compose入门示例：一键部署 Nginx+Tomcat+Mysql

    整体环境配置 整体环境的配置,如果一个一个 Dockerfile 去写,那么是相当麻烦的,好在 Docker 有一个名为 Docker-Compose 的工具提供,我们可以使用它一次性完成整体环境的配 ...