Python小练习之验证“哥德巴赫猜想”
设计内容:任何一个大于2的偶数都可以分解为两个素数之和,这就是著名的哥达巴赫猜想。
设计要求:要求输入一个大于2的偶数,程序运行后,输出两个素数,其和正好等于该偶数。
1. 实验代码(知道是你们最喜欢的,直接放前面)
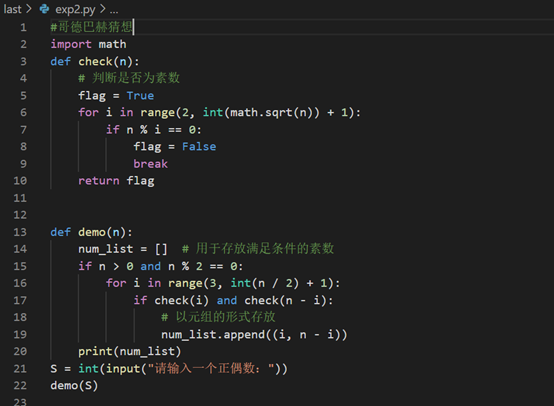
2. 设计思路
首先要接受一个正偶数,赋值S,然后找到两个素数,其和为S,那么就要有判断素数的函数,定义函数check()判断。根据素数定义,除了1和本身都不能除开判断。然后还需要输出符合条件的素数。因为可能不止一组,所以选择了以元组的方式存储。讲最初接收到S调用demo()函数,来输出。
3.运行结果

Python小练习之验证“哥德巴赫猜想”的更多相关文章
- PTA实验4-2-3 验证“哥德巴赫猜想” (20分)
实验4-2-3 验证"哥德巴赫猜想" (20分) 数学领域著名的"哥德巴赫猜想"的大致意思是:任何一个大于2的偶数总能表示为两个素数之和.比如:24=5+19, ...
- c语言验证哥德巴赫猜想(从4开始 一个偶数由两个质数之和)
#include <stdio.h> #include <stdlib.h> #include <math.h> int isit(int num) { int i ...
- 洛谷P1579.验证哥德巴赫猜想(DFS+素性测试)
题目背景 1742年6月7日哥德巴赫写信给当时的大数学家欧拉,正式提出了以下的猜想:任何一个大于9的奇数都可以表示成3个质数之和.质数是指除了1和本身之外没有其他约数的数,如2和11都是质数,而6不是 ...
- C语言验证哥德巴赫猜想
#include<stdio.h>int f(int x);int main(void){ int n,i; scanf("%d",&n); for( ...
- Java实现蓝桥杯算法提高 哥德巴赫猜想
试题 算法提高 哥德巴赫猜想 资源限制 时间限制:1.0s 内存限制:256.0MB 问题描述 根据所给函数(判断一个整数是否是素数),然后依托该函数,将输入N内的偶数(6-N),输出为两个素数之和( ...
- Java实现哥德巴赫猜想
验证哥德巴赫猜想:任何一个大于 6 的偶数,都能分解成两个质数的和.要求输入一个整数,输出这个 数能被分解成哪两个质数的和. eg : 14 14=3+11 14=7+7 public class T ...
- Python练习:哥德巴赫猜想
哥德巴赫猜想 哥德巴赫 1742 年给欧拉的信中哥德巴赫提出了以下猜想:任一大于 2 的偶数都可写成两个质数之和.但是哥德巴赫自己无法证明它,于是就写信请教赫赫有名的大数学家欧拉帮忙证明,但是一直到死 ...
- Codeforces Round #324 (Div. 2) D. Dima and Lisa 哥德巴赫猜想
D. Dima and Lisa Time Limit: 1 Sec Memory Limit: 256 MB 题目连接 http://codeforces.com/contest/584/probl ...
- python 验证码 高阶验证
python 验证码 高阶验证 标签: 验证码python 2016-08-19 15:07 1267人阅读 评论(1) 收藏 举报 分类: 其他(33) 目录(?)[+] 字符型图片验证 ...
随机推荐
- PHP的CLI命令行运行模式浅析
在做开发的时候,我们不仅仅只是做各种网站或者接口,也经常需要写一些命令行脚本用来处理一些后端的事务.比如对数据进行处理统计等.当然也是为了效率着想,当一个事务有可能会有较长的耗时时,往往会交由服务器的 ...
- JMeter主要元件
配置元件 http cookie管理器 http信息头管理器 http请求默认值 统一管理 快速切换测试环境 http cache管理器 静态资源 监听器元件 查看结果树 分析查看某个请求的详情 请求 ...
- P7515-[省选联考 2021A卷]矩阵游戏【差分约束】
正题 题目链接:https://www.luogu.com.cn/problem/P7515 题目大意 有一个\(n*m\)的矩形\(A\),然后给出一个\((n-1)*(m-1)\)的矩形\(B\) ...
- 什么?你还不明白自动化的POM设计模式?
POM简介.POM优势.如何设计POM POM简介 Page Object Model (POM) 直译为"页面对象模型",这种设计模式旨在为每个待测试的页面创建一个页面对象(cl ...
- python OSError: [Errno 22] Invalid argument: '\u202aF://text
windows10 python3 读文件的时候报的错误 原因不明时好时坏很头疼但又没办法不知道怎么解决,网上的说法都不能解决,
- ASP.NET Core 学习笔记 第二篇 依赖注入
前言 ASP.NET Core 应用在启动过程中会依赖各种组件提供服务,而这些组件会以接口的形式标准化,这些组件这就是我们所说的服务,ASP.NET Core框架建立在一个底层的依赖注入框架之上,它使 ...
- 【LeetCode】300.最长递增子序列——暴力递归(O(n^3)),动态规划(O(n^2)),动态规划+二分法(O(nlogn))
算法新手,刷力扣遇到这题,搞了半天终于搞懂了,来这记录一下,欢迎大家交流指点. 题目描述: 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度. 子序列是由数组派生而来的序列,删除(或不删 ...
- 阿里限流神器Sentinel夺命连环 17 问?
1.前言 这是<spring Cloud 进阶>专栏的第五篇文章,这篇文章介绍一下阿里开源的流量防卫兵Sentinel,一款非常优秀的开源项目,经过近10年的双十一的考验,非常成熟的一款产 ...
- bzoj2242,洛谷2485----SDOI2011计算器(exgcd,qsm,bsgs模板)
就是一道模板题! 这里再强调一下 BSGS 考虑方程\(a^x = b \pmod p\) 已知a,b,p\((2 \le p\le 10^9)\),其中p为质数,求x的最小正整数解 解法: 注意到如 ...
- UltraSoft - Alpha - Scrum Meeting 8
Date: Apr 23th, 2020. Scrum 情况汇报 进度情况 组员 负责 昨日进度 后两日任务 CookieLau PM.后端 aliyun连接前后端,跑通demo 实现邮箱注册的验证码 ...
