What Makes for Good Views for Contrastive Learning

概
前
InfoMin
构建 novel views
- 无监督
- 半监督

Tian Y., Sun C., Poole B., Krishnan D., Schmid C. & Isola P. What Makes for Good Views for Contrastive Learning? arXiv preprint arXiv 2005.10243, 2020.

概

是什么使得对比学习有效, 对比学习的关键之处是什么? 本文设计了很多巧妙的实验来说明这一点.

前

一般的对比学习, 通过是构造俩个随机变量$v_1, v_2$, 然后通过InfoNCE损失来区分开联合分布$p(v_1, v_2)$以及$p(v_1)p(v_2)$（也是互信息所衡量的指标),

\[\mathcal{L}_{NCE} = - \mathbb{E} [\log \frac{e^{h(v_{1,i}v_{2,i})}}{\sum_{j=1}^K e^{h(v_{1, i}, v_{2, j})}}],
\]

其中$h(\cdot, \cdot)$通常是包含两个encoders$f_{v_1},f_{v_2}$, 以及project head $h$. 最小化NCE损失实际上是在最大化互信息的一个上界

\[I(v_1;v_2) \ge \log K - \mathcal{L}_{NCE} =: I_{NCE}(v_1;v_2).
\]

$I_{NCE}(v_1;v_2)$在下面将作为互信息的一个替代出现.

充分Encoder: 称$f_1$关于$v_1$是充分的, 如果$I(v_1, v_2) = I(f_1(v_1);v_2)$, 即经过特征提取后, 并没有丢失与$v_2$的共享的信息.

最小充分Encoder: 称$f_1$为$v_1$的最小充分Encoder, 如果$I(f_1(v_1), v_1) \le I(f(v_1); v_1)$对任意的充分Encoder$f$成立, 即我们希望一个好的encoder能够撇去非共享的信息(我们认为是噪声).

最优表示: 对于分类任务$\mathcal{T}$来说, 从$x$中预测类别标签$y$的$x$最优特征表示$z^*$为$y$的最小充分统计量.

注:

充分统计量定义: 一个函数$T(X)$被称之为一族概率分布$\{f_{\theta}(x)\}$的充分统计量, 如果给定$T(X)=t$时$X$的条件分布与$\theta$无关, 即

\[f_{\theta}(x) = f(x|t) f_{\theta}(t) \Rightarrow \theta \rightarrow T(X) \rightarrow X \Rightarrow I(\theta;T(X)) \ge I(\theta;X).
\]

此时, $I(\theta;T(X))= I(\theta;X)$.

最小充分统计量定义: 如果一个充分统计量$T(X)$与其余的一切关于$\{f_{\theta}(x)\}$的充分统计量$U(X)$满足

\[\theta \rightarrow T(X) \rightarrow U(X) \rightarrow X.
\]

用这里的话表述就是

\[p(x, z|y) = p(x|z)p(z|y) \Rightarrow x \rightarrow z \rightarrow y \Rightarrow I(z;y) = I(x;y).
\]

同时

\[y \rightarrow z^* \rightarrow z \rightarrow x.
\]

上面加了自己的理解, 但是我对这理解有信心.

InfoMin

Proposition4.1: 假设$f_1, f_2$为两最小充分encoders(分别关于$v_1, v_2$). 给定下游任务$\mathcal{T}$和即对应的标签$y$, 则最优的$v$应当满足

\[(v_1^*, v_2^*) = \min_{v_1, v_2} I(v_1;v_2), \quad \mathrm{s.t.}\: I(v_1;y) = I(v_2;y)=I(x;y),
\]

此时, 最优的特征表示$z_1^*, z_2^*$关于$\mathcal{T}$是最优的.

这个主张可以很直观地去理解, 即假设我们的encoder足够好: 在保留$v_1, v_2$的共享信息的同时, 能够撇去大量的无关信息, 则最优的views 应该在不丢失标签信息的前提下, 二者的共享信息越少.

$v_1, v_2$应当有足够的共享信息用于下游任务；
$v_1, v_2$之间共享的信息越少越好, 即共享信息最好仅仅与下游任务有关, 无别的噪声;

为此, 作者举了一个相当有趣的例子:

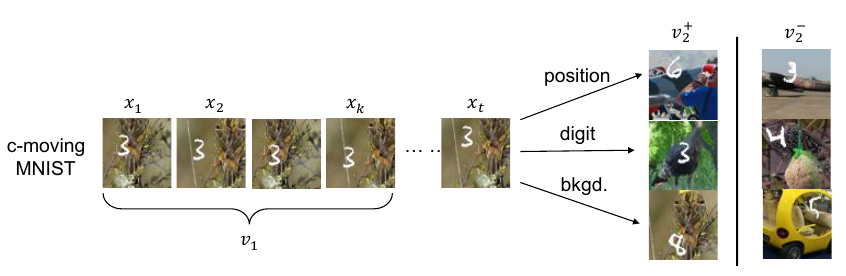
数字, 在某个随机背景上以一定速度移动, 这个数据集有三个要素:

什么数字;
数字的位置;
背景;

左边的$v_1$即为普通的view, 右边$v_2^+$是对应的正样本, 所构成的三组正样本对分别共享了

数字的位置;
数字;
背景;

三个信息, 其余两个要素均是随机选择, 故正样本也仅共享了对应要素的信息. 负样本对的各要素均是随机选择的.

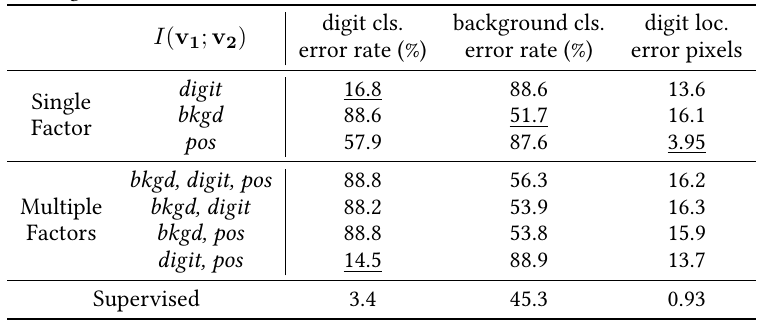
实验结果如上表, 如果像文中所表述的, 正样本对仅关注某一个要素, 则用于下游任务(即判别对应的元素, 如判别出数字, 判别出背景, 判别出数字的位置), 当我们关注哪个要素的时候, 哪个要素的下游任务的效果就能有明显提升(注意数字越小越好).

本文又额外做了同时关注多个要素的实验, 实验效果却并不理想, 往往是背景这种更为明显, 更占据主导的地位的共享信息会被对比损失所关注.

这个实验是上述主张的一个有力验证.

Sweet Spot

现在的InfoNCE损失, 其目的是最大化互信息的一个下界, 那么这个下界也就是$I_{NCE}$是否越大越好呢?

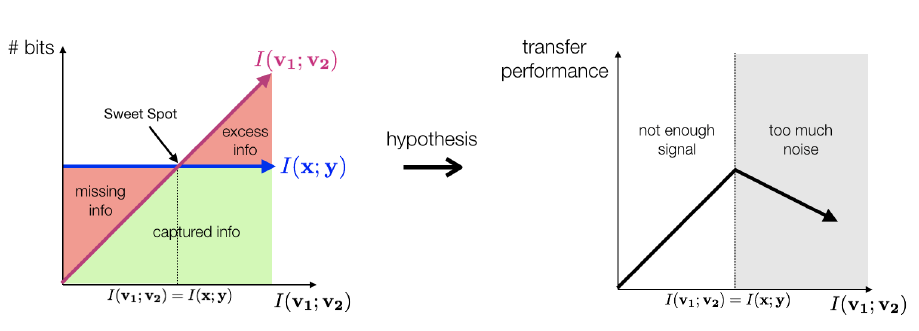
上面这个图有些奇怪, 不过其大致表示的含义是:

$I(v_1;v_2)< I(x;y)$, 则增大二者的互信息是有利于下游任务的;
$I(v_1;v_2) = I(x;y)$的时候, 即二者共享的信息恰为用于下游任务所需的信息时, 效果最佳;
$I(v_1;v_2) > I(x; y)$继续增大二者的互信息, 实际上是在增加噪声, 这不利于提取到好的特征.

故随着$v_1, v_2$二者的互信息的增加, 特征迁移的效果应该是呈现一个倒U的形状.

作者通过不同的augmentation方法来验证.

空间距离

作者从一个大图上, 分别从$(x, y)$和$(x+d, y+d)$, $d \in [64, 384]$作为起点截取大小为$64\times64$的patch作为样本对, 显然$d$越大二者的互信息越小, 最后用于分类任务的结果:

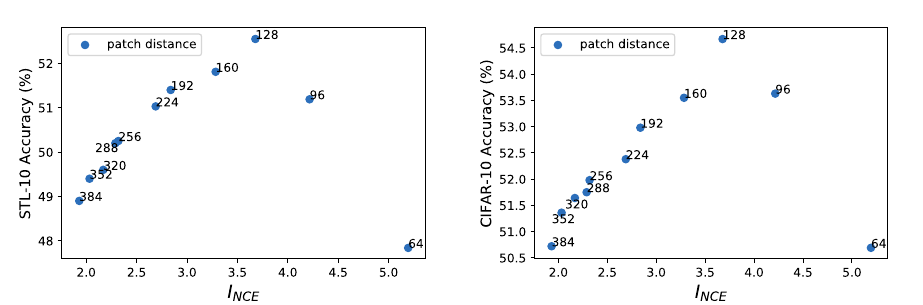
这是很明显的倒U.

Color Spaces

作者又尝试了不同的color spaces分割作为构建样本对的依据:

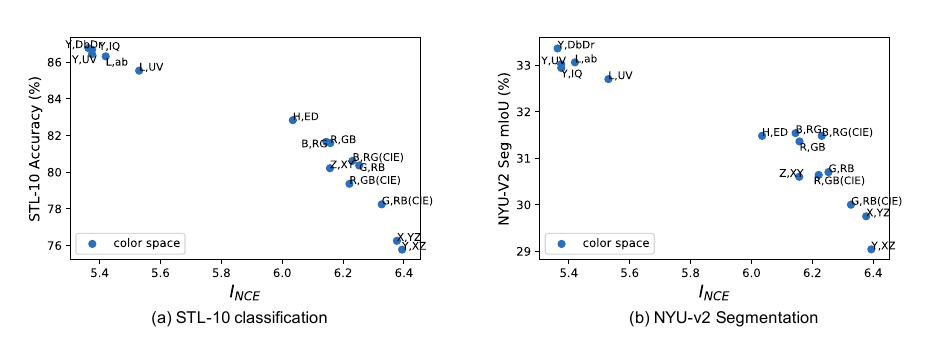
同样有类似的结果.

没有呈现倒U是因为单纯的分割没法让$I_{NCE}$变得太小.

Frequency Separation

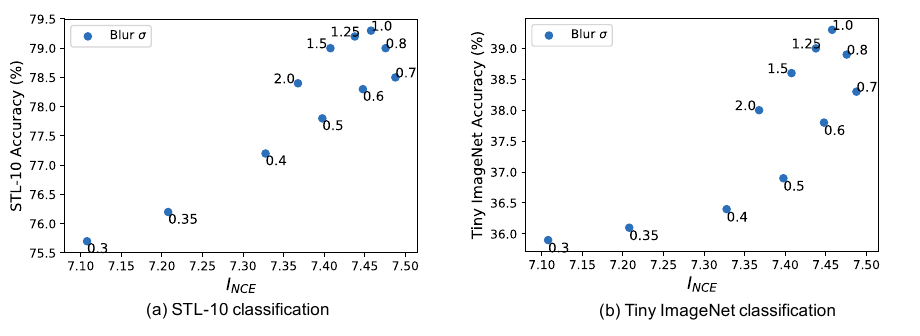
构建 novel views

作者紧接着, 提出了一些构造 novel views 的办法. 正如前面已经提到过的, novel views $v_1,v_2$应当是二者仅共享一些与下游任务有关的信息, 抓住这个核心.

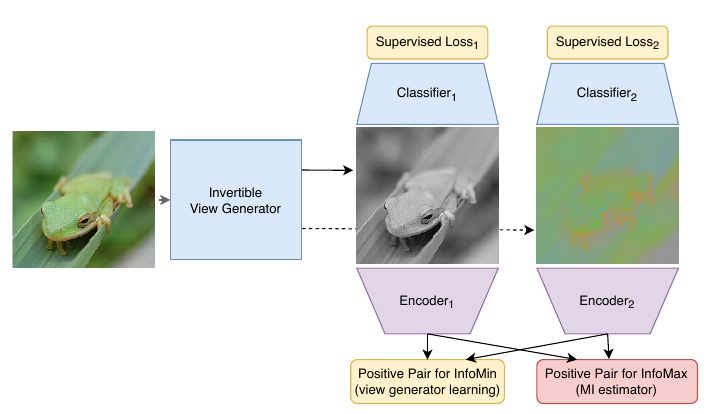
无监督

\[\min_g \max_{f_1, f_2} I_{NCE}^{f_1, f_2} (g(X)_1, g(X)_{2:3}),
\]

其中$g$是一个生成器, 将$X$映射为相同大小的$X'$, 然后选取$v_1=X_1', v_2 = X_{2:3}’$，$f_1, f_2$是两个encoder. 这个思路和GAN很像, 就是希望$g$将$v_1, v_2$之间的互信息压缩, 但是$f$要将提高二者的互信息.

注: 个人认为有点奇怪, 因为我觉得上面的$f_1, f_2$对$g$并没有牵制作用, $g$完全可以生成噪声, 这样不就令$I_{NCE}$很小了? 所以$g$的网络不能太复杂?

半监督

正如我上面注提到的问题, 原来作者也注意到了这个问题, 并希望借助标签信息来破解

\[\min_{g,c_1, c_2} \max_{f_1, f_2} I_{NCE}^{f_1, f_2} (g(X)_1; g(X)_{2:3}) + \mathcal{L}_{ce} (c_1(g(X)), y) + \mathcal{L_{ce}}(c_2(g(X)_{2:3}), y),
\]

即除上面提到的外, 我们希望$g$转换后的图片, 能够用于分类, 这样一来, $g$就不得不生成一些具有意义的图片. 称之为半监督的原因是, 分类误差可以仅作用于有标签的数据集.

注: 感觉分类任务可以直接替换成下游任务, 虽然有种画蛇添足的感觉.