决策树 机器学习,西瓜书p80 表4.2 使用信息增益生成决策树及后剪枝
使用信息增益构造决策树,完成后剪枝
1 构造决策树
1 根结点的选择
色泽 信息增益
根据色泽划分为 青绿,乌黑,浅白 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D^2) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Ent(D^3)&= -(\frac{2}{2} log_2 \frac{2}{2}+\frac{0}{2} log_2 \frac{0}{2})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,色泽)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{4}{10}\times 1+\frac{4}{10} \times 0.811+\frac{2}{10}\times0) \\
&= 0.2756\end{aligned}
\]
根蒂 信息增益
根据根蒂划分为 蜷缩 稍蜷 硬挺 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{5} log_2 \frac{2}{5}+\frac{3}{5} log_2 \frac{3}{5})=0.971 \\
Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{5}{10}\times 0.971+\frac{4}{10} \times 1+\frac{1}{10}\times0) \\
&= 0.1145\end{aligned}
\]
敲声 信息增益
根据色泽划分为 浊响,沉闷,清脆 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{6} log_2 \frac{2}{6}+\frac{4}{6} log_2 \frac{4}{6})=0.918 \\
Ent(D^2) &= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{1}{3} log_2 \frac{1}{3})=0.918 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,敲声)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{6}{10}\times 0.918+\frac{3}{10} \times 0.918+\frac{1}{10}\times0) \\
&=0.2346\end{aligned}
\]
纹理 信息增益
根据 纹理 划分为 清晰 稍糊 模糊 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{2}{6} log_2 \frac{2}{6}+\frac{4}{6} log_2 \frac{4}{6})=0.918 \\
Ent(D^2) &= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{1}{3} log_2 \frac{1}{3})=0.918 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,纹理)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{6}{10}\times 0.918+\frac{3}{10} \times 0.918+\frac{1}{10}\times0) \\
&= 0.2346\end{aligned}
\]
脐部 信息增益
根据色泽划分为 凹陷,稍凹,平坦 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D^3)&= -(\frac{2}{2} log_2 \frac{2}{2}+\frac{0}{2} log_2 \frac{0}{2})=0 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,脐部)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{4}{10}\times 0.811+\frac{4}{10} \times 1+\frac{2}{10}\times0) \\
&= 0.2756\end{aligned}
\]
触感 信息增益
根据色泽划分为 硬滑,软粘 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{3}{6} log_2 \frac{3}{6}+\frac{3}{6} log_2 \frac{3}{6})=1 \\
Ent(D^2) &= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Ent(D)&= -(\frac{5}{10} log_2 \frac{5}{10}+\frac{5}{10} log_2 \frac{5}{10})=1 \\
Gani(D,触感)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{6}{10}\times 1 +\frac{4}{10} \times 1 \\
&= 0\end{aligned}
\]
选择根结点构建决策树
\[\begin{aligned}
Gain(D,色泽)=0.2756 \ Gain(D,根蒂)=0.1145 \ Gain(D,敲声)=0.2346 \\
Gain(D,纹理)=0.2346 \ Gain(D,脐部)=0.2756 \ Gain(D,触感)=0\end{aligned}
\]
比较六个属性的信息增益大小,选择脐部作为根结点
则数据集被划分为
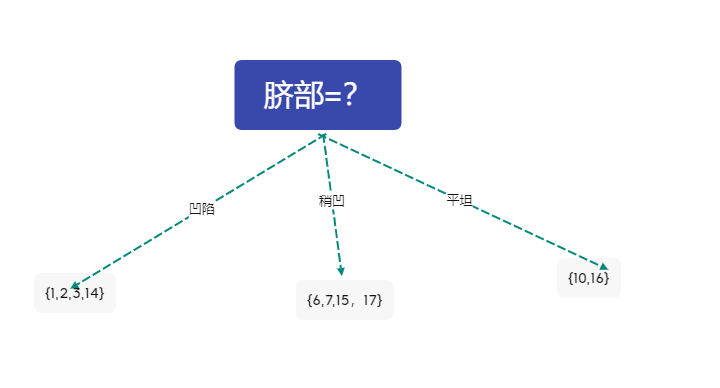
2 对分支结点\({1,2,3,14}\)进行划分
色泽 信息增益
根据色泽划分为 青绿,乌黑,浅白 三个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\
Ent(D^2) &= -(\frac{0}{2} log_2 \frac{0}{2}+\frac{2}{2} log_2 \frac{2}{2})=0 \\
Ent(D^3)&= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Gani(D,色泽)&=Ent(D)-\sum_{v=1}^3 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 - (\frac{1}{4}\times 0+\frac{2}{4} \times 0 +\frac{1}{4}\times 0) \\
&= 0.811\end{aligned}
\]
根蒂 信息增益
根据根蒂划分为 蜷缩 稍蜷 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{3} log_2 \frac{0}{3}+\frac{3}{3} log_2 \frac{3}{3})=0 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})= 0.811\\
Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 - (\frac{3}{4}\times 0 +\frac{1}{4} \times 0) \\
&= 0.811\end{aligned}
\]
敲声 信息增益
根据色泽划分为 浊响,沉闷 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{2} log_2 \frac{0}{2}+\frac{2}{2} log_2 \frac{2}{2})=0 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Gani(D,敲声)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 - (\frac{2}{4}\times 0 +\frac{2}{4} \times 1 ) \\
&=0.311\end{aligned}
\]
纹理 信息增益
根据 纹理 划分为 清晰 稍糊 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{3} log_2 \frac{0}{3}+\frac{3}{3} log_2 \frac{3}{3})=0 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 - (\frac{3}{4}\times 0+\frac{1}{4} \times 0 ) \\
&= 0.811\end{aligned}
\]
触感 信息增益
根据触感划分为 硬滑 一个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})=0.811 \\
Ent(D)&= -(\frac{1}{4} log_2 \frac{1}{4}+\frac{3}{4} log_2 \frac{3}{4})= 0.811 \\
Gani(D,触感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.811 - (\frac{4}{4}\times 0.811 ) \\
&= 0\end{aligned}
\]
选择分类结点构建决策树
\[\begin{aligned}
Gain(D,色泽)=0.811 \ Gain(D,根蒂)=0.811 \ Gain(D,敲声)=0.311 \\
Gain(D,纹理)=0.811 \ \ \ Gain(D,触感)=0\end{aligned}
\]
不妨选择色泽作为分类依据
形成的决策树
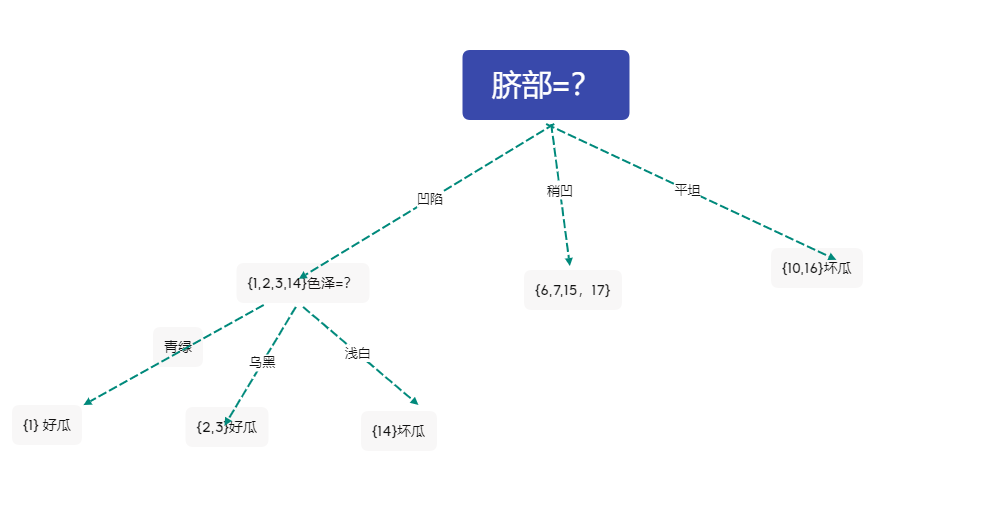
3 对分支 \({6,7,15,17}\)进行划分
色泽 信息增益
根据色泽划分为 青绿,乌黑 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{0}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})= 1 \\
Gani(D,色泽)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{2}{4}\times 1+\frac{2}{4} \times 1 ) \\
&= 0\end{aligned}
\]
根蒂 信息增益
根据根蒂划分为 蜷缩 稍蜷 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0。918\\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\
Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})= 1\\
Gani(D,根蒂)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{3}{4}\times 0.918 +\frac{1}{4} \times 0) \\
&= 0.3115\end{aligned}
\]
敲声 信息增益
根据色泽划分为 浊响,沉闷 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})= 0 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Gani(D,敲声)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{3}{4}\times 0.918 +\frac{1}{4} \times 0 ) \\
&=0.3115\end{aligned}
\]
纹理 信息增益
根据 纹理 划分为 清晰 稍糊 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{2}{4}\times 1+\frac{2}{4} \times 1 ) \\
&= 0\end{aligned}
\]
触感 信息增益
根据触感划分为 硬滑,软粘 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0 \\Ent(D)&= -(\frac{2}{4} log_2 \frac{2}{4}+\frac{2}{4} log_2 \frac{2}{4})=1 \\
Gani(D,触感)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{3}{4}\times 0.918+\frac{1}{4} \times 0 ) \\
&= 0.2295\end{aligned}
\]
选择分类结点构建决策树
\[\begin{aligned}
Gain(D,色泽)=0 \ Gain(D,根蒂)=0.3115 \ Gain(D,敲声)=0.3115 \\
Gain(D,纹理)=0 \ \ \ Gain(D,触感)=0.2295\end{aligned}
\]
不妨选择根蒂作为分类依据
此时决策树为
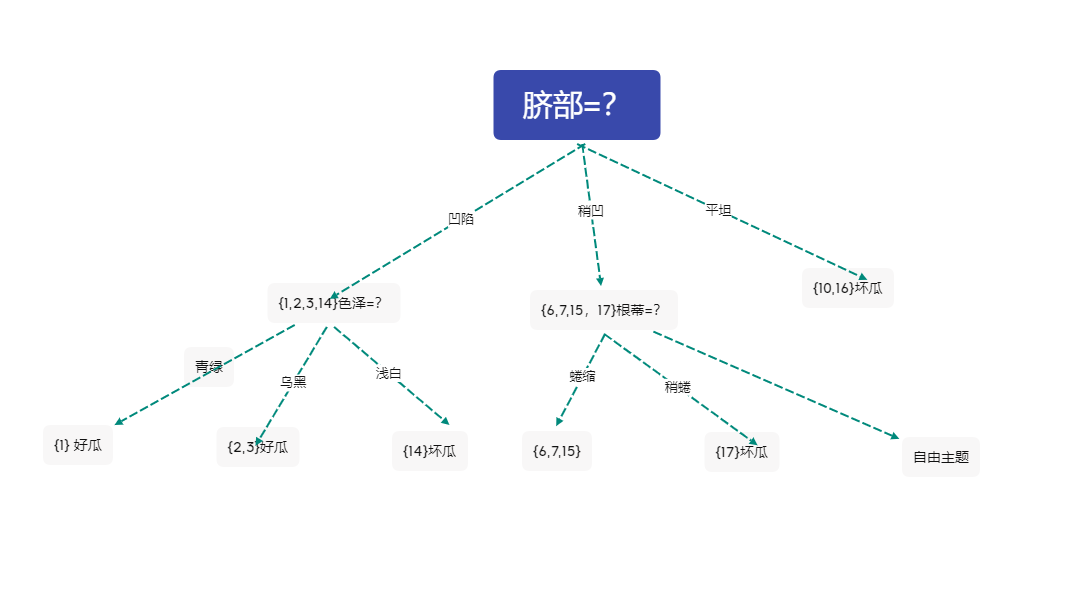
4 对分支\({6,7,15}\)进行划分
色泽 信息增益
根据色泽划分为 青绿,乌黑 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\
Ent(D^2) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})= 0.918 \\
Gani(D,色泽)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 - (\frac{1}{3}\times 0+\frac{2}{3} \times 1 ) \\
&= 0.252\end{aligned}
\]
敲声 信息增益
根据色泽划分为 浊响 一个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\Ent(D)&= -(\frac{2}{3} log_2 \frac{2}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Gani(D,敲声)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 - (\frac{3}{3}\times 0.918 ) \\
&=0\end{aligned}
\]
纹理 信息增益
根据 纹理 划分为 清晰 稍糊 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Ent(D^2) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0\\Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\
Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 - (\frac{2}{3}\times 1+\frac{1}{3} \times 0 ) \\
&= 0.252\end{aligned}
\]
触感 信息增益
根据触感划分为 软粘 一个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918 \\Ent(D)&= -(\frac{1}{3} log_2 \frac{1}{3}+\frac{2}{3} log_2 \frac{2}{3})=0.918\\
Gani(D,触感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 0.918 - (\frac{3}{3}\times 0.918 ) \\
&= 0\end{aligned}
\]
选择分类结点构建决策树
\[\begin{aligned}
Gain(D,色泽)=0 .252 \ \ Gain(D,敲声)=0 \\
Gain(D,纹理)=0.252 \ \ \ Gain(D,触感)=0\end{aligned}
\]
不妨选择色泽作为分类依据
此时决策树为
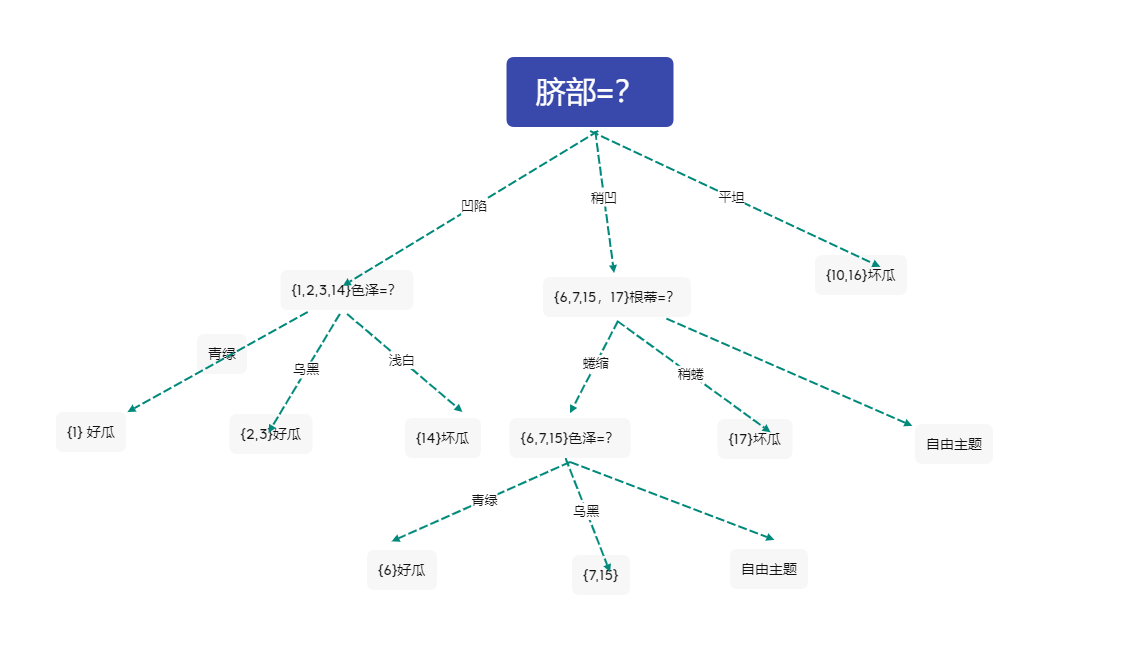
5 对分支\({7,15}\)进行划分
敲声 信息增益
根据色泽划分为 浊响 一个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1\\
Gani(D,敲声)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{2}{2}\times 0.918 ) \\
&= 0\end{aligned}
\]
纹理 信息增益
根据 纹理 划分为 清晰 稍糊 两个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{0}{1} log_2 \frac{0}{1}+\frac{1}{1} log_2 \frac{1}{1})=0 \\
Ent(D^2) &= -(\frac{1}{1} log_2 \frac{1}{1}+\frac{0}{1} log_2 \frac{0}{1})=0\\Ent(D)&= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\
Gani(D,纹理)&=Ent(D)-\sum_{v=1}^2 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{1}{2}\times 0+\frac{1}{2} \times 0 ) \\
&= 1\end{aligned}
\]
触感 信息增益
根据触感划分为 软粘 一个子集
计算信息熵
\[\begin{aligned}
Ent(D^1) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1 \\Ent(D) &= -(\frac{1}{2} log_2 \frac{1}{2}+\frac{1}{2} log_2 \frac{1}{2})=1\\
Gani(D,触感)&=Ent(D)-\sum_{v=1}^1 \frac{|D^v|}{|D|}Ent(D^v) \\
&= 1 - (\frac{2}{2}\times 0.918 ) \\
&= 0\end{aligned}
\]
选择分类结点构建决策树
\[\begin{aligned}
\ \ Gain(D,敲声)=0 \ Gain(D,纹理)=1 \ \ \ Gain(D,触感)=0\end{aligned}
\]
选择纹理作为分类依据
此时决策树为
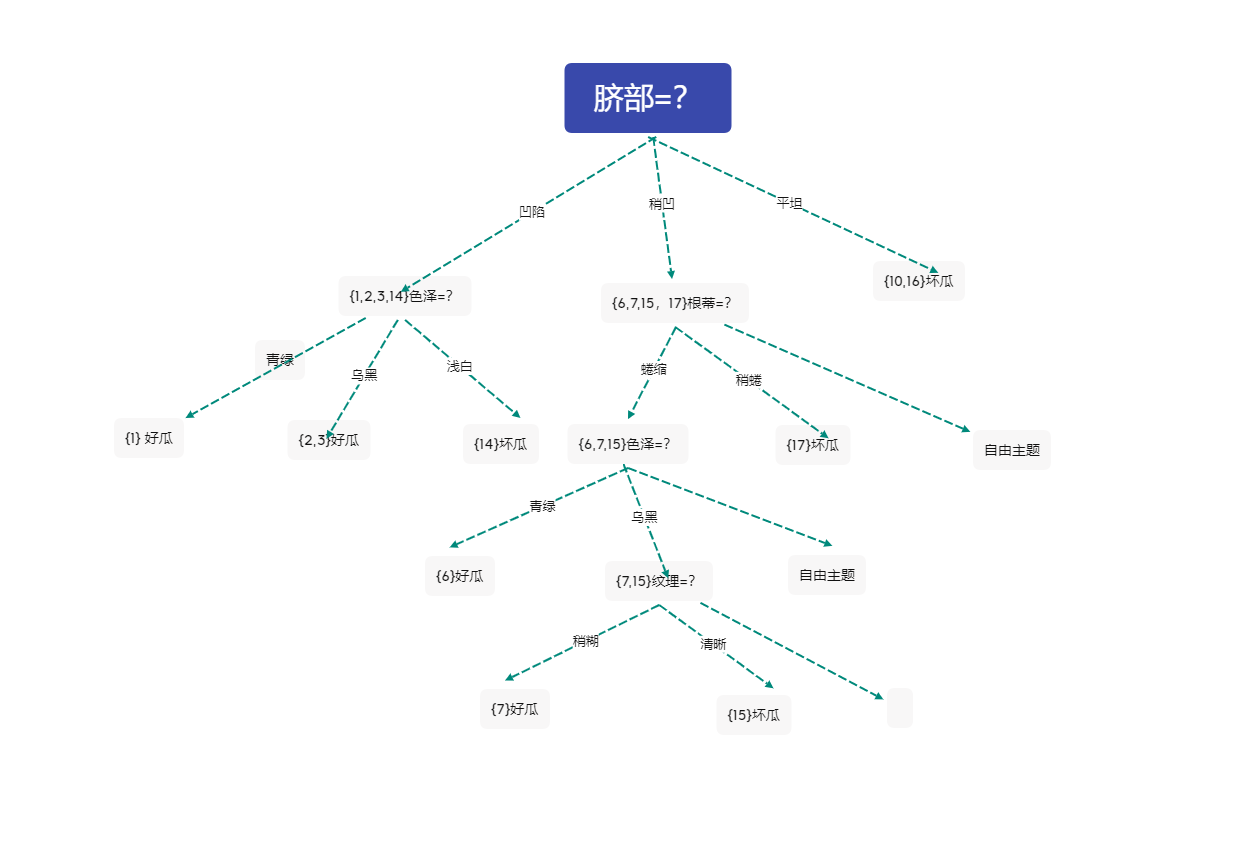
2 决策树后剪枝
1 考虑结点\(7,15\)
原分支(剪枝前),有三个样本被正确分类 验证集精度为 42.8%
剪枝后的决策树
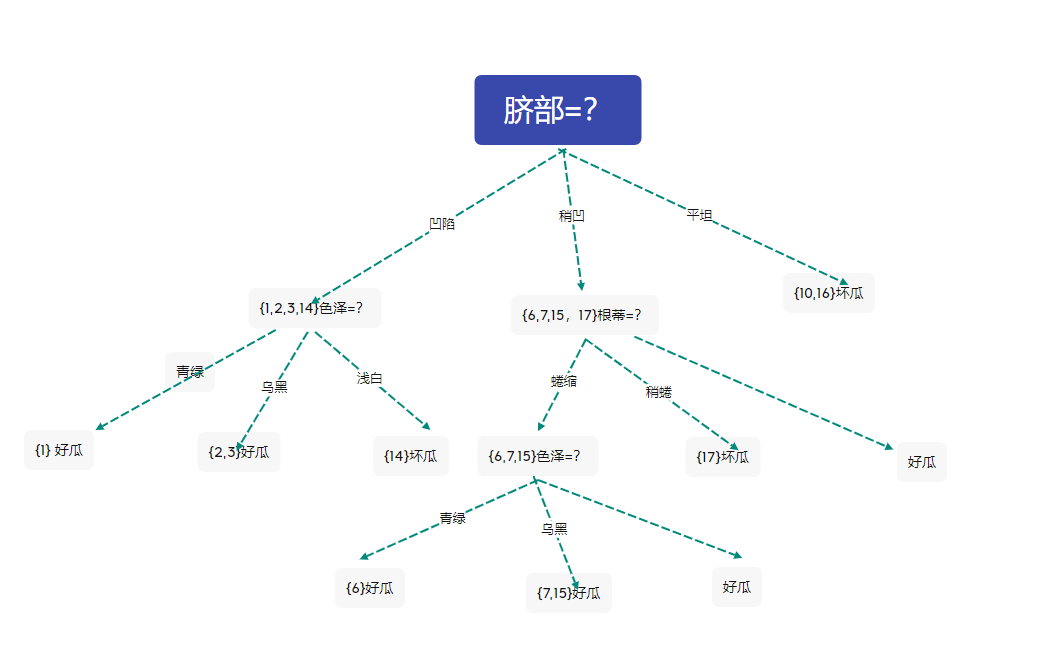
此时验证集有四个样本被正确分类,精度为57.1%
于是后剪枝策略决定剪枝,得到上图的决策树
2 考虑结点\(6,715\)色泽=?
由上图,决策树精度为57.1%
剪去结点后的决策树为
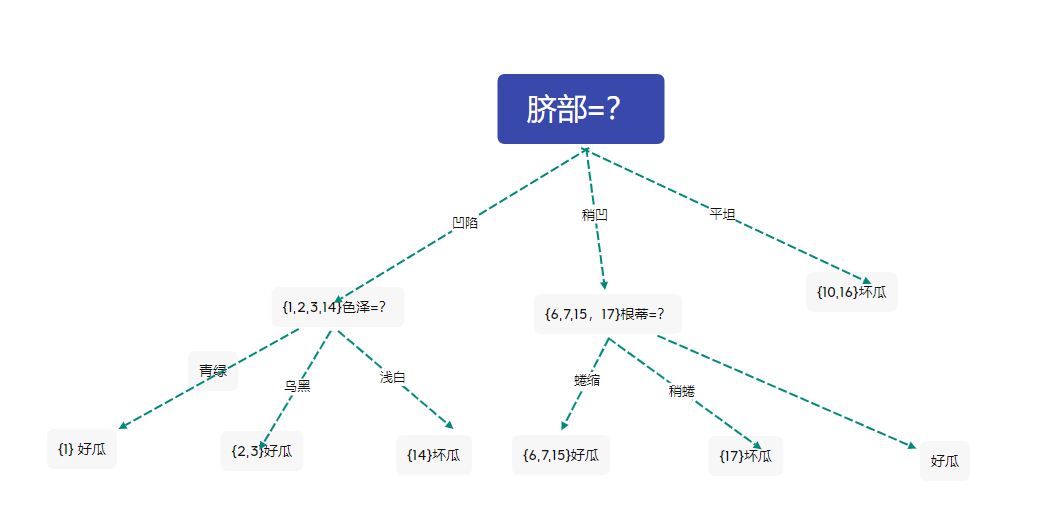
此时验证集有四个样本被正确分类,精度为57.1%
与未剪枝时的精度相同,西瓜书中采用了不剪枝的策略。在这里我们不妨采用剪枝的策略,于是得到上图的决策树
3 考虑结点\(1,2,3,14\)色泽=?
在上图基础上来考虑剪去结点\(1,2,3,14\)色泽=? ,剪枝后的决策树为
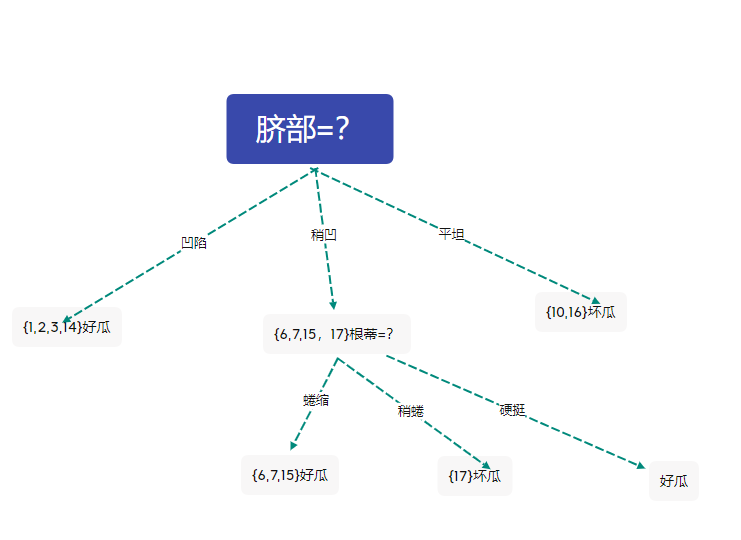
此时的决策树正确分类的样本5个,精度为71.4%
根据后剪枝策略,进行剪枝,得到上图的决策树
4考虑 \(6,7,15,17\)根蒂=?
剪枝后的决策树为
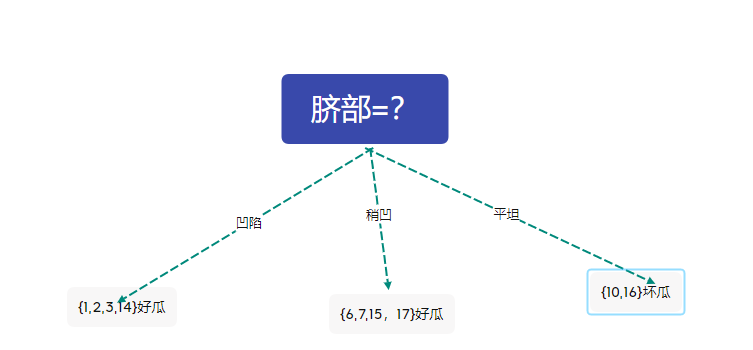
此时的决策树的精度仍然为71.4%
与未剪枝时的精度相同,西瓜书中采用了不剪枝的策略。在这里我们不妨采用剪枝的策略,于是得到上图的决策树
最终得到上图的决策树
决策树 机器学习,西瓜书p80 表4.2 使用信息增益生成决策树及后剪枝的更多相关文章
- 周志华-机器学习西瓜书-第三章习题3.5 LDA
本文为周志华机器学习西瓜书第三章课后习题3.5答案,编程实现线性判别分析LDA,数据集为书本第89页的数据 首先介绍LDA算法流程: LDA的一个手工计算数学实例: 课后习题的代码: # coding ...
- python实现简单决策树(信息增益)——基于周志华的西瓜书数据
数据集如下: 色泽 根蒂 敲声 纹理 脐部 触感 好瓜 青绿 蜷缩 浊响 清晰 凹陷 硬滑 是 乌黑 蜷缩 沉闷 清晰 凹陷 硬滑 是 乌黑 蜷缩 浊响 清晰 凹陷 硬滑 是 青绿 蜷缩 沉闷 清晰 ...
- 决策树ID3原理及R语言python代码实现(西瓜书)
决策树ID3原理及R语言python代码实现(西瓜书) 摘要: 决策树是机器学习中一种非常常见的分类与回归方法,可以认为是if-else结构的规则.分类决策树是由节点和有向边组成的树形结构,节点表示特 ...
- (二)《机器学习》(周志华)第4章 决策树 笔记 理论及实现——“西瓜树”——CART决策树
CART决策树 (一)<机器学习>(周志华)第4章 决策树 笔记 理论及实现——“西瓜树” 参照上一篇ID3算法实现的决策树(点击上面链接直达),进一步实现CART决策树. 其实只需要改动 ...
- LASSO回归与L1正则化 西瓜书
LASSO回归与L1正则化 西瓜书 2018年04月23日 19:29:57 BIT_666 阅读数 2968更多 分类专栏: 机器学习 机器学习数学原理 西瓜书 版权声明:本文为博主原创文章,遵 ...
- 朴素贝叶斯python代码实现(西瓜书)
朴素贝叶斯python代码实现(西瓜书) 摘要: 朴素贝叶斯也是机器学习中一种非常常见的分类方法,对于二分类问题,并且数据集特征为离散型属性的时候, 使用起来非常的方便.原理简单,训练效率高,拟合效果 ...
- 手把手生成决策树(dicision tree)
手把手生成决策树(dicision tree) 标签: Python 机器学习 主要參考资料: Peter HARRINGTON.机器学习实战[M].李锐,李鹏,曲亚东,王斌译.北京:人民邮电出版社, ...
- GZFramwork数据库层《二》单据表增删改查(自动生成单据号码)
运行效果: 使用代码生成器(GZCodeGenerate)生成tb_EmpLeave的Model 生成器源代码下载地址: https://github.com/GarsonZhang/GZCodeGe ...
- Javascript_06_表单验证(离开单项,输入框后提示信息)
Javascript_06_ 表单验证(离开单项,输入框后提示信息) 说明:对于必须输入的入力框,光标离开(使用 onblur方法)时进行检查.假如有错,红色的提示信息直接在该画面的这个输入框的后面显 ...
随机推荐
- CodeForce-797C Minimal string(贪心模拟)
Minimal string CodeForces - 797C Petya 收到一个长度不超过 105 的字符串 s.他拿了两个额外的空字符串 t 和 u 并决定玩一个游戏.这个游戏有两种合法操作: ...
- OC源码剖析对象的本质
1. 类的底层实现 先写一个 Person 类: @interface Person : NSObject @property (nonatomic, copy) NSString *p_name; ...
- 博客主题-Next风格
适配方法 下载压缩包,按照文件名将内容复制粘贴到对应框中即可. 注意事项 请将主题设置为custom 禁用默认css 下载连接 Next.rar version:2020-07-10 next.rar ...
- 查看Docker启动jenkins的管理员密码
Docker启动docker后,第一次方法jenkins,需要输入管理员密码. 其实查看启动时候的日志可以看到密码,也可以按照以下方法找到密码. 1.查看docker容器ID:docker ps -a ...
- sql case when 多条件小结
sql case when 多条件 小结 -- 第一种 格式 : 简单Case函数 : -- 格式说明 -- case 列名 -- when 条件值1 then 选择项1 -- when 条件值2 t ...
- 分享一个设计logo的网站
https://editor.freelogodesign.org/
- 鸿蒙内核源码分析(原子操作篇) | 是谁在为原子操作保驾护航 | 百篇博客分析OpenHarmony源码 | v34.02
百篇博客系列篇.本篇为: v34.xx 鸿蒙内核源码分析(原子操作篇) | 谁在为原子操作保驾护航 | 51.c.h .o 本篇说清楚原子操作 读本篇之前建议先读鸿蒙内核源码分析(总目录)系列篇. 基 ...
- go语言游戏服务端开发(四)——RPC机制
五邑隐侠,本名关健昌,12年游戏生涯. 本教程以Go语言为例. RPC指远程方法调用,游戏里引入RPC目的是降低跨进程交互的复杂度. 游戏业务设计为多go routine,一个玩家一个go routi ...
- ubuntu20.04安装网易云音乐
Ubuntu20.04安装网易云 进入网易云音乐下载地址 下载对应客户端 进入终端,安装 sudo dpkg -i 软件名.deb
- Serverless 如何在阿里巴巴实现规模化落地?
作者 | 赵庆杰(卢令) 来源 | Serverless 公众号 一.Serverless 规模化落地集团的成果 2020 年,我们在 Serverless 底层基建上做了非常大的升级,比如计算升级到 ...
