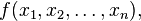梯度、Hessian矩阵、平面方程的法线以及函数导数的含义
本文转载自:
Xianling Mao的专栏
===========================================================================
想必单独论及“ 梯度、Hessian矩阵、平面方程的法线以及函数导数”等四个基本概念的时候,绝大部分人都能够很容易地谈个一二三,基本没有问题。
其实在应用的时候,这几个概念经常被混淆,本文试图把这几个概念之间的关系整理一下,以便应用之时得心应手。
这四个概念中,Hessian矩阵是最不容易混淆,但却是很多人难以记住的概念,其它三个概念很容易记住,但却在某些时候很容易混淆。
- Hessian矩阵:设有凸函数f(X),X是向量(x1,x2,..., xn),Hessian矩阵M定义为:M的第i行,第j列元素为df(X)/dxidxj, 即为f(X)对于变量xi和xj的二次偏导数。
- 梯度:设有凸函数f(X),X是向量(x1,x2,..., xn),函数f(X)在点X0处的梯度是一个向量,等于(df(X0)/dx1, df(X0)/dx2, ...., df(X0)/dxn), 即是对于各个变量的偏导数的向量。例子:如果方程是z=f(x,y),梯度是在XOY平面内的一个向量,与z无关。因此要特别注意梯度不是点(X,f(X))处的切线方向。
- 平面方程的法线:设平面方程Ax+By+Cz+D = 0,向量(A, B, C)为这个平面的法线方向。
- 函数导数:二维直线的方程y= kx+b,我们说k是直线的斜率;二维曲线y=f(x)的导数f '(x)表示在点x处的切线的斜率,注意是切线的斜率,不是切线的方向,它是标量,不是向量。任意曲线y=f(x1,x2,...xn),对每一个变量求取偏导数,得到一个向量(df(X)/dx1, df(X)/dx2, ...., df(X)/dxn),这个向量就是函数在点X处的梯度,即梯度是表示曲线f(X)在X处变化最剧烈的方向,特别注意梯度并不是在点(X, f(X))处的切线方向, 梯度只是在点(X, f(X))处的切线方向在X构成的“平面”上的投影。注意,对于二维直线y=kx+b,它也是可以求取梯度的,它的梯度是向量(k),只有一个值,表示的是x方向上的向量,大小是x方向上的单位变化导致y变化量的大小,即就是切线的斜率。
以下内容转载自:http://blog.sina.com.cn/s/blog_662234020100q2vh.html,谢谢!
在数学中,海塞矩阵(Hessian matrix 或 Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,此函数如下:
如果 f 所有的二阶导数都存在,那么 f 的海塞矩阵即:
- H(f)ij(x) = DiDjf(x)
其中 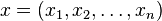 ,即
,即
二阶偏导数矩阵也就所谓的海赛矩阵(Hessian matrix)
一元函数就是二阶导,多元函数就是二阶偏导组成的矩阵
求向量函数最小值时用的,矩阵正定是最小值存在的充分条件。
经济学中常常遇到求最优的问题,目标函数是多元非线性函数的极值问题尚无一般的求解方法,但判定局部极小值的方法是有的,就是用海赛矩阵,是变量向量二阶偏导数构成的矩阵,矩阵正定是局部极小点的充分条件。
梯度、Hessian矩阵、平面方程的法线以及函数导数的含义的更多相关文章
- 【机器学习】梯度、Hessian矩阵、平面方程的法线以及函数导数的含义
想必单独论及" 梯度.Hessian矩阵.平面方程的法线以及函数导数"等四个基本概念的时候,绝大部分人都能够很容易地谈个一二三,基本没有问题. 其实在应用的时候,这几个概念经常被混 ...
- 梯度vs Jacobian矩阵vs Hessian矩阵
梯度向量 定义: 目标函数f为单变量,是关于自变量向量x=(x1,x2,-,xn)T的函数, 单变量函数f对向量x求梯度,结果为一个与向量x同维度的向量,称之为梯度向量: 1. Jacobian 在向 ...
- 三维重建面试4:Jacobian矩阵和Hessian矩阵
在使用BA平差之前,对每一个观测方程,得到一个代价函数.对多个路标,会产生一个多个代价函数的和的形式,对这个和进行最小二乘法进行求解,使用优化方法.相当于同时对相机位姿和路标进行调整,这就是所谓的BA ...
- Jacobian矩阵、Hessian矩阵和Newton's method
在寻找极大极小值的过程中,有一个经典的算法叫做Newton's method,在学习Newton's method的过程中,会引入两个矩阵,使得理解的难度增大,下面就对这个问题进行描述. 1, Jac ...
- Hessian矩阵与牛顿法
Hessian矩阵与牛顿法 牛顿法 主要有两方面的应用: 1. 求方程的根: 2. 求解最优化方法: 一. 为什么要用牛顿法求方程的根? 问题很多,牛顿法 是什么?目前还没有讲清楚,没关系,先直观理解 ...
- Hessian矩阵【转】
http://blog.sina.com.cn/s/blog_7e1ecaf30100wgfw.html 在数学中,海塞矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,一元函数就是二阶导, ...
- C#处理医学图像(一):基于Hessian矩阵的血管肺纹理骨骼增强对比
在医院实际环境中,经常遇到有问题的患者,对于一些特殊的场景,比如骨折,肺结节,心脑血管问题 需要图像对比增强来更为清晰的显示病灶助于医生确诊,先看效果: 肺纹理增强: 肺结节增强: 血管对比增强: 骨 ...
- Jacobian矩阵和Hessian矩阵
1.Jacobian矩阵 在矩阵论中,Jacobian矩阵是一阶偏导矩阵,其行列式称为Jacobian行列式.假设 函数 $f:R^n \to R^m$, 输入是向量 $x \in R^n$ ,输出为 ...
- Hessian矩阵
http://baike.baidu.com/link?url=o1ts6Eirjn5mHQCZUHGykiI8tDIdtHHOe6IDXagtcvF9ncOfdDOzT8tmFj41_DEsiUCr ...
随机推荐
- docker安装笔记
Docker 是一个开源的应用容器引擎,让开发者可以打包他们的应用以及依赖包到一个可移植的镜像中,然后发布到任何流行的 Linux或Windows 机器上,也可以实现虚拟化.容器是完全使用沙箱机制,相 ...
- ES分布式原理
参考:https://blog.csdn.net/chang384915878/article/details/86747419 一.准备知识 这里只是简单的介绍,详情可以看我的另一篇博客:https ...
- 玩转Android状态栏
前言 前段时间,突然收到一个状态栏颜色优化设计的任务,将原本应用整体的黑色状态栏修改为根据标题栏颜色进行沉浸式设计,显示效果如下: image 经过分析及踩过N多坑,终于完成了APP全局的修改.现 ...
- MyCAT与MySQL导入、导出文件
1. MySQL批量导入-LOAD DATA使用本地客户端连接MySQL数据库,批量导入数据,出现报错:2017-06-07 09:30:45,936 MySqlWrapper::ImportCSVt ...
- python自动化测试—配置文件的使用
一.什么是配置文件? 配置文件示例 [mysql] default-character-set = utf8 [mysqld] port = 3306 basedir = c:\mysql-5.7.2 ...
- yum 问题
[root@localhost ~]# yum update There are no enabled repos. Run "yum repolist all" to see t ...
- htmlunit与Jsoup
//这个函数的目的是在获取页面的同时,也获取链接对应的cookiepublic static HtmlPage getCookieAndHtml(String url)throws IOExcepti ...
- PHP中替换换行符的几种方法
PHP中替换换行的几种方法 参考脚本之家的文章:<PHP中替换换行符的几种方法小结>. 代码: 方法一: $replace_str = str_replace(array("\r ...
- C语言字符串追加,双色球等案例
//C语言中没有字符串概念,有的只是字符型数组,以str1[]的值为例,该字符数组的长度为11--->包含了字母,空格,以及结束字符'\0'(斜杠0)//基于上述原因,读取一个字符型数组的有效方 ...
- layui中从子窗口传递数据到父窗口,第三个子弹层的值传给第二个弹层
最近做一个项目的需要多个弹层,每个弹层中还需要数据传递, 经过测试,以下方法三个弹层才有效,如果只是有两个弹层,请用其它方法 大概如图,看图自己应该明白 如何在在b页面选择好的值传给a页面的问题,这个 ...