#5 DIV2 A POJ 3321 Apple Tree 摘苹果 构建线段树

Apple Tree

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 25232		Accepted: 7503

Description

There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

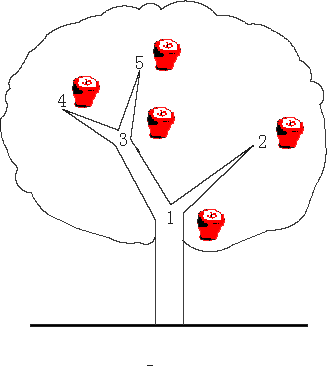
The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

Input

The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
"C x" which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
"Q x" which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning

Output

For every inquiry, output the correspond answer per line.

Sample Input

3
1 2
1 3
3
Q 1
C 2
Q 1

Sample Output

3
2

Source

POJ Monthly--2007.08.05, Huang, Jinsong

题意：给你一颗n个节点的树，每个节点开始有一个苹果，然后m次修改，每次修改使得某个节点的苹果改变，有变成没有，没有变成有。询问的是某个节点及其子树的苹果数目。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <vector>
#include <queue>
#include <stack>
#include <map>
#include <algorithm>
#include <set>
using namespace std;
typedef long long ll;
typedef unsigned long long Ull;
#define MM(a,b) memset(a,b,sizeof(a));
const double eps = 1e-10;
const int  inf =0x7f7f7f7f;
const double pi=acos(-1);
const int maxn=100000+10;

int dfs_clock=0,vis[4*maxn],s[4*maxn],e[4*maxn];
vector<vector<int> > G(4*maxn);
struct node{
   int l,r,val,flag;
   int mid(){
      return (l+r)>>1;
   }
}tree[4*maxn];

void push_up(int k)
{
   tree[k].val=tree[2*k].val+tree[2*k+1].val;
}

void build(int k,int l,int r)
{
    tree[k].l=l;tree[k].r=r;
    if(l==r) {tree[k].val=1;return;}
    build(2*k,l,(l+r)/2);
    build(2*k+1,(l+r)/2+1,r);
    push_up(k);
}

void dfs(int u)
{
    dfs_clock++;
    vis[u]=1;
    s[u]=dfs_clock;
    for(int i=0;i<G[u].size();i++)
    {
        int v=G[u][i];
        if(vis[v]) continue;
        dfs(v);
    }
    e[u]=dfs_clock;
}

void update(int k,int pos)
{
    if(tree[k].l==tree[k].r) {tree[k].val^=1;return;}
    if(pos<=tree[k].mid()) update(2*k,pos);
    else update(2*k+1,pos);
    push_up(k);
}

int query(int k,int l,int r)
{
    if(l<=tree[k].l&&tree[k].r<=r)
        return tree[k].val;
    else if(tree[k].r>=l&&tree[k].l<=r)
    {
        int res=0;
        res+=query(2*k,l,r);
        res+=query(2*k+1,l,r);
        return res;
    }
    else return 0;
}

int main()
{
    int n,m;
    while(~scanf("%d",&n))
    {
        MM(vis,0);
        for(int i=1;i<=n;i++) G[i].clear();
        for(int i=1;i<=n-1;i++)
        {
            int u,v;
            scanf("%d %d",&u,&v);
            G[u].push_back(v);
            G[v].push_back(u);
        }
        dfs_clock=0;
        dfs(1);
        build(1,1,n);

        scanf("%d",&m);
        for(int i=1;i<=m;i++)
        {
            char a[3];int x;
            scanf("%s %d",a,&x);
            if(a[0]=='Q')  printf("%d\n",query(1,s[x],e[x]));
            else  update(1,s[x]);
        }
    }
    return 0;
}

　　分析：线段树很好的一道题，比赛的时候想到了单点更新维护区间和，所以应该要线段树或BIT，但是

这棵树连二叉树都不是，就不知道怎么维护了，，，，这也是这道题的精华所在，首先dfs一次，依据

时间戳，得出每个节点维护的区间，这样子节点维护的区间必然被父节点包含，然后就是常规的线段树了，

单点更新时就只要更新该点所在时间戳的那个点，这样包含该点的区间的值也会相应修改，查询某点

及其子树的值，就只要查询这个点对应的区间就好，神奇的一题