数学--数论--HDU - 6395 Let us define a sequence as below 分段矩阵快速幂

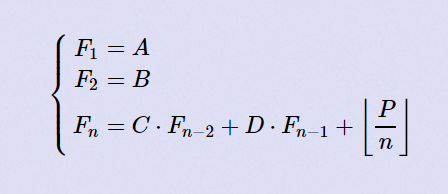
Your job is simple, for each task, you should output Fn module 109+7.

Input

The first line has only one integer T, indicates the number of tasks.

Then, for the next T lines, each line consists of 6 integers, A , B, C, D, P, n.

1≤T≤200≤A,B,C,D≤1091≤P,n≤109

Output

36

24

Sample Input

2

3 3 2 1 3 5

3 2 2 2 1 4

Sample Output

36

24

首先处理递推式这里，因为直接递推会超时，我们考虑矩阵快速幂，然后看题，有三个未知量，我们构造3*3的矩阵，然后因为还有一个数论分块，不能直接使用矩阵快速幂，应该相等的位置使用矩阵快速幂，然后完事了

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod = 1e9+7;
int a, b, c, d, p, n, t;

struct mat{
	int m[3][3];
	mat(){
		memset(m, 0, sizeof(mat));
	}
	friend mat operator*(mat a, mat b){
		mat c;
		for(int i=0; i<3; i++){
			for(int j=0; j<3; j++){
				ll t = 0;
				for(int k=0; k<3; k++){
					t += (ll)a.m[i][k]*b.m[k][j];
				}
				c.m[i][j] = t%mod;
			}
		}
		return c;
	}
}I;

mat pow_mat(mat a, int b){
	mat c = I;
	while(b){
		if(b&1){
			c = c*a;
		}
		a = a*a;
		b >>= 1;
	}
	return c;
}

int main(){
	I.m[0][0] = I.m[1][1] = I.m[2][2] = 1;
	scanf("%d", &t);
	while(t--){
		scanf("%d%d%d%d%d%d", &a, &b, &c, &d, &p, &n);
		if(n == 1){
			printf("%d\n", a);
			continue;
		}
		mat f;
		f.m[0][0] = d;
		f.m[0][1] = c;
		f.m[1][0] = 1;
		f.m[2][2] = 1;
		int flag = 0;
		for(int i=3; i<=n;){
			if(p/i == 0){
				mat w = f;
				w = pow_mat(w, n-i+1);
				ll ans = w.m[0][0]*(ll)b%mod + w.m[0][1]*(ll)a + w.m[0][2]%mod;
				ans %= mod;
				printf("%lld\n", ans);
				flag = 1;
				break;
			}
			int j = min(n, p/(p/i));
			mat w = f;
			w.m[0][2] = p/i;
			w = pow_mat(w, j-i+1);
			ll tmp1 = (w.m[1][0]*(ll)b + w.m[1][1]*(ll)a + w.m[1][2]) % mod;
			ll tmp2 = (w.m[0][0]*(ll)b + w.m[0][1]*(ll)a + w.m[0][2]) % mod;
			a = tmp1; b = tmp2;
			i = j+1;
		}
		if(!flag)
			printf("%d\n", b);
	}

}