[模板]最小割树(Gomory-Hu Tree)(luogu4897)

给定一个\(n\)个点\(m\)条边的无向连通图，多次询问两点之间的最小割

两点间的最小割是这样定义的：原图的每条边有一个割断它的代价，你需要用最小的代价使得这两个点不连通

Input

第一行两个数\(n,m\)

接下来\(m\)行，每行3个数\(u,v,w\)，表示有一条连接\(u\)与\(v\)的无向边，割断它的代价为\(w\)

接下来这一行有一个整数\(Q\)，表示询问次数

接下来\(Q\)行，每行两个数\(u,v\),你需要求出\(u\)与\(v\)之间的最小割

Output

输出共\(Q\)行，每行一个整数对应询问的答案

Sample Input

4 5
1 2 2
2 3 2
4 2 3
4 3 1
1 3 1
3
1 4
2 4
2 3

Sample Output

3
4
4

Hint

\(n\leq 500,\quad m\leq 1500,\quad Q\leq 10^5,\quad 0\leq w\leq 10^4\)

题意：

求任意两点间的最小割（最大流）

题解：

本题要用到最小割树。

最小割树其实就是把所有的点分成多个部分然后分治，使只用跑很少次网络流就能解决两点之间的最小割。

举个例子：

这个图：



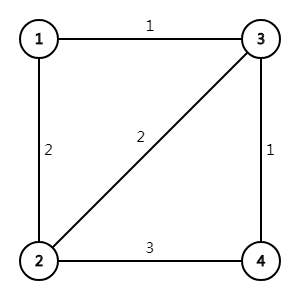
开始先求1，4点间的最小割，易得为3。

跑完网络流之后的图是这样的。



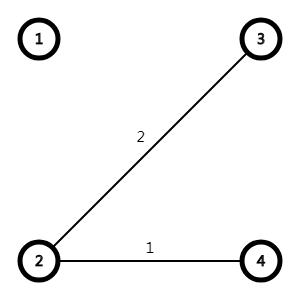
我们发现图变成了两部分，事实上，图肯定会变成两部分甚至更多，因为既然是一个割，就肯定会把两个点分到不同的区域。

然后易知两个区域之间的最小割至少为当前的最小割——3。

当前\(ans\)为

\[\begin{matrix}
0 & 3 & 3 & 3 \\
3 & 0 & inf & inf \\
3 & inf & 0 & inf \\
3 & inf & inf & 0
\end{matrix}
\]

然后我们把图复原



在刚才划分的区域里继续划分

但有(1)区间只剩一个点了，所以不继续划分，取（2，3，4）中的2，3两点做最小割(其实随便哪两个不同的点都可以)，易得最小割为4。



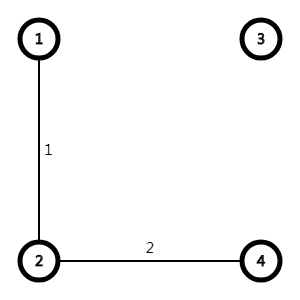
然后易知两个区域之间的最小割至少为当前的最小割——4。

然后更新答案，记住，就算不在当前区间内的数也必须更新。

当前\(ans\)为

\[\begin{matrix}
0 & 3 & 3 & 3 \\
3 & 0 & 4 & inf \\
3 & 4 & 0 & 4 \\
3 & inf & 4 & 0
\end{matrix}
\]

继续复原，更新，然后得到最后的\(ans\)：

\[\begin{matrix}
0 & 3 & 3 & 3 \\
3 & 0 & 4 & 4 \\
3 & 4 & 0 & 4 \\
3 & 4 & 4 & 0
\end{matrix}
\]

然后就可以根据询问输出了。

用这样的算法只用跑\(n\)遍网络流，因为每次必定分离两个点，乘上网络流复杂度\(O(n^2m)\)(其实跑不满)复杂度是\(O(n^3m)\)(也跑不满)。

至于为什么叫最小割树，大概是因为实际运算的时候每次都会把区间分为两部分，所以会分\(n-1\)次，然后每次会算出一个数（最小割），可以作为边权，然后就成了一棵树。

听说在这棵树上跑倍增找路径上的最小值也可以做这道题。

#include<bits/stdc++.h>
#define re register
using namespace std;
const int inf=1<<29,N=1010,M=20010;
int n,m,a[N];
int ans[N][N];
int head[N],nxt[M],bian[M],zhi[M],tot;
void init(){
    tot=1;
    memset(head,0,sizeof head);
}
inline void add(re int x,re int y,re int z){
    tot++;bian[tot]=y;zhi[tot]=z;nxt[tot]=head[x];head[x]=tot;
    tot++;bian[tot]=x;zhi[tot]=z;nxt[tot]=head[y];head[y]=tot;
}
inline void build(int m){
    for(re int i=1;i<=m;i++){
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
    }
}
void rebuild(){
    for(re int i=1;i<=tot;i+=2){
        zhi[i]=zhi[i^1]=(zhi[i]+zhi[i^1])>>1;
    }
}
int v[N],d[N];
void cut(int x){
    v[x]=1;
    for(int i=head[x];i;i=nxt[i]){
        if(zhi[i]&&!v[bian[i]])cut(bian[i]);
    }
}
queue<int>q;
bool bfs(int b,int e){
    memset(d,0,sizeof(d));
    while(!q.empty())q.pop();
    q.push(b);d[b]=1;
    while(!q.empty()){
        int x=q.front();q.pop();
        for(int i=head[x];i;i=nxt[i]){
            if(zhi[i] && !d[bian[i]]){
                q.push(bian[i]);
                d[bian[i]]=d[x]+1;
                if(bian[i]==e)return 1;
            }
        }
    }
    return 0;
}
int dinic(int b,int e,int x,int flow){
    if(x==e)return flow;
    int rest=flow,k;
    for(int i=head[x];i && rest;i=nxt[i]){
        if(zhi[i] && d[bian[i]]==d[x]+1){
            k=dinic(b,e,bian[i],min(rest,zhi[i]));
            if(!k)d[bian[i]]=0;
            zhi[i]-=k;
            zhi[i^1]+=k;
            rest-=k;
        }
    }
    return flow-rest;
}
inline int maxflow(int b,int e){
    int flow=0,maxflow=0;
    while(bfs(b,e)){
        while(flow=dinic(b,e,b,inf))maxflow+=flow;
    }
    return maxflow;
}
int b,e;
void solve(int l,int r){
    if(l==r)return;
    rebuild();
    b=a[l],e=a[r];
    re int mincut=maxflow(b,e);
    memset(v,0,sizeof v);
    cut(b);
    for(re int i=1;i<=n;++i){
        if(!v[i])continue;
        for(re int j=1;j<=n;++j){
            if(v[j])continue;
            ans[i][j]=ans[j][i]=min(ans[i][j],mincut);
        }
    }
    re int cnt=l-1;
    static int ls[N];
    for(re int i=l;i<=r;++i){
        if(v[a[i]]){
            ls[++cnt]=a[i];
        }
    }
    re int fj=cnt;
    for(re int i=l;i<=r;++i){
        if(!v[a[i]]){
            ls[++cnt]=a[i];
        }
    }
    for(re int i=l;i<=r;++i)a[i]=ls[i];
    solve(l,fj);
    solve(fj+1,r);
}
int main()
{
    int b,e,q;
    memset(ans,0x3f,sizeof ans);
    cin>>n>>m;
    init();
    build(m);
    for(int i=1;i<=n;++i){
    	a[i]=i;
    }
    solve(1,n);
    cin>>q;
    while(q--){
        scanf("%d%d",&b,&e);
        if(ans[b][e]==0x3f3f3f3f)ans[b][e]=2147483647;
        printf("%d\n",ans[b][e]);
    }
}