梯度下降（Gradient Descent）相关概念

梯度，直观理解：

梯度: 运算的对像是纯量,运算出来的结果会是向量在一个标量场中,

梯度的计算结果会是"在每个位置都算出一个向量,而这个向量的方向会是在任何一点上从其周围(极接近的周围,学过微积分该知道甚么叫极限吧?)标量值最小处指向周围标量值最大处.而这个向量的大小会是上面所说的那个最小与最大的差距程度"

举例子来讲会比较简单,如果现在的纯量场用一座山来表示,纯量值越大的地方越高,反之则越低.经过梯度这个运操作数的运算以后,会在这座山的每一个点上都算出一个向量,这个向量会指向每个点最陡的那个方向,而向量的大小则代表了这个最陡的方向到底有多陡.

梯度下降的直观理解：简而言之，就是下山不知道路怎么走，就走一步算一步

重要概念：

梯度下降（Gradient Descent）小结

如下图，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

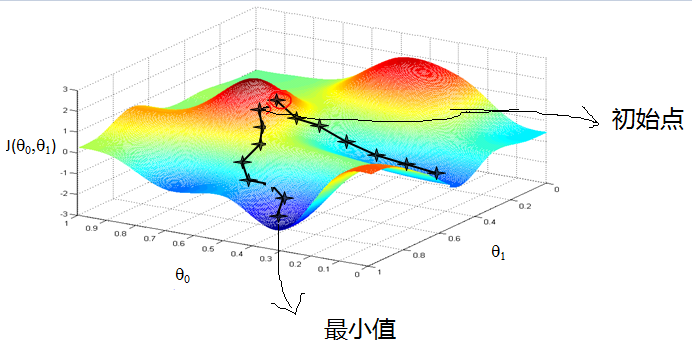
在详细了解梯度下降的算法之前，我们先看看相关的一些概念。

　　　　1. 步长（Learning rate）：步长决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度。用上面下山的例子，步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。

　　　　2.特征（feature）：指的是样本中输入部分，比如样本（x₀,y₀）,（x₁,y₁）,则样本特征为x，样本输出为y。

　　　　3. 假设函数（hypothesis function）：在监督学习中，为了拟合输入样本，而使用的假设函数，记为h_θ(x)。比如对于样本（x_i,y_i）(i=1,2,...n),可以采用拟合函数如下： h_θ(x) = θ₀+θ₁x。

　　　　4. 损失函数（loss function）：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。比如对于样本（x_i,y_i）(i=1,2,...n),采用线性回归，损失函数为：

\(J(\theta_0, \theta_1) = \sum\limits_{i=1}^{m}(h_\theta(x_i) - y_i)^2\)

　　　　其中\(x_i\)表示样本特征x的第i个元素，\(y_i\)表示样本输出y的第i个元素，\(h_\theta(x_i)\)为假设函数。

Cost Function

Cost Function的用途：对假设的函数进行评价，cost function越小的函数，说明拟合训练数据拟合的越好；

下图详细说明了当cost function为黑盒的时候，cost function 的作用；

但是我们肯定想知道cost Function的内部构造是什么？因此我们下面给出公式：

其中：

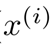表示向量x中的第i个元素；

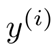表示向量y中的第i个元素；

表示已知的假设函数；

m为训练集的数量；

比如给定数据集(1,1)、(2,2)、(3,3)
则x = [1;2;3]，y = [1;2;3] （此处的语法为Octave语言的语法，表示3*1的矩阵）
如果我们预测theta0 = 0，theta1 = 1，则h(x) = x，则cost function：
J(0,1) = 1/(2*3) * [(h(1)-1)^2+(h(2)-2)^2+(h(3)-3)^2] = 0；
如果我们预测theta0 = 0，theta1 = 0.5，则h(x) = 0.5x，则cost function：
J(0,0.5) = 1/(2*3) * [(h(1)-1)^2+(h(2)-2)^2+(h(3)-3)^2] = 0.58；