Proximal Gradient Descent for L1 Regularization(近端梯度下降求解L1正则化问题)

假设我们要求解以下的最小化问题： $min_xf(x)$

如果$f(x)$可导，那么一个简单的方法是使用Gradient Descent (GD)方法，也即使用以下的式子进行迭代求解：

$x_{k+1} = x_k - a\Delta f(x_k)$

如果$\Delta f(x)$满足L-Lipschitz，即：

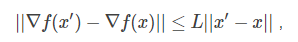
那么我们可以在点$x_k$附近把$f(x)$近似为：

把上面式子中各项重新排列下，可以得到：

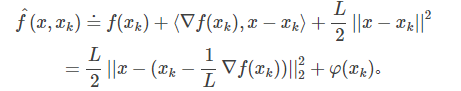
这里$\varphi (x_k)$不依赖于x，因此可以忽略。

显然，$\hat f(x, x_k)$的最小值在

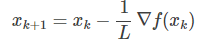获得。所以，从这个角度看的话，GD的每次迭代是在最小化原目标函数的一个二次近似函数.（梯度下降的由来的推导,这里说的不好，参考这里： http://www.cnblogs.com/ljygoodgoodstudydaydayup/p/7274943.html）

在很多最小化问题中，我们往往会加入非光滑的惩罚项$g(x)$, 比如常见的L1惩罚: $g(x) = ||x||_1$ .这个时候，GD就不好直接推广了。但上面的二次近似思想却可以推广到这种情况：

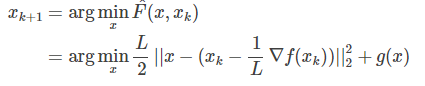
这就是所谓的Proximal Gradient Descent （PGD）算法,即目标函数由损失项和正则项组成。对于上式，可先计算$z = x_k - \frac{1}{L}\Delta f(x_k)$, 然后求解

---

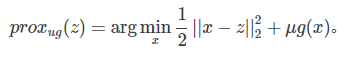
软阈值(SoftThresholding)可以求解如下优化问题：

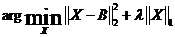
其中：

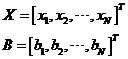
根据范数的定义，可以将上面优化问题的目标函数拆开：

也就是说，我们可以通过求解N个独立的形如函数

的优化问题，来求解这个问题。由中学时代学过的求极值方法知道，可以求函数f(x)导数：

令函数f(x)导数等于0，得：

这个结果等号两端都有变量x，需要再化简一下。下面分三种情况讨论：

(1)当b>λ/2时

假设x<0，则sgn(x)=-1，所以x=b+λ/2>0，与假设x<0矛盾；（λ > 0）

假设x>0，则sgn(x)=1，所以x=b-λ/2>0，成立；

所以此时在x=b-λ/2>0处取得极小值：

即此时极小值小于f(0)，而当x<0时

即当x<0时函数f(x)为单调降函数（对任意△x<0，f(0)<f(△x)）。因此，函数在x=b-λ/2>0处取得最小值。

(2)当b<-λ/2时

假设x<0，则sgn(x)=-1，所以x=b+λ/2<0，成立；

假设x>0，则sgn(x)=1，所以x=b-λ/2<0，与假设x>0矛盾；

所以此时在x=b+λ/2<0处取得极小值：

即此时极小值小于f(0)，而当x>0时

即当x>0时函数f(x)为单调升函数（对任意△x>0，f(△x)>f(0)）。因此，函数在x=b+λ/2<0处取得最小值。

(3)当-λ/2<b<λ/2时(即|b|<λ/2时)

假设x<0，则sgn(x)=-1，所以x=b+λ/2>0，与假设x<0矛盾；

假设x>0，则sgn(x)=1，所以x=b-λ/2<0，与假设x<0矛盾；

即无论x为大于0还是小于0均没有极值点，那么x=0是否为函数f(x)的极值点呢？

对于△x≠0，

当△x >0时，利用条件b<λ/2可得

当△x <0时，利用条件b<λ/2可得(注：此时|△x |=-△x)

因此，函数在x=0处取得极小值，也是最小值。

综合以上三种情况，f(x)的最小值在以下位置取得：

至此，我们可以得到优化问题

的解为

http://blog.csdn.net/bingecuilab/article/details/50628634

http://blog.csdn.net/jbb0523/article/details/52103257