P3990 [SHOI2013]超级跳马

传送门

首先不难设\(f[i][j]\)表示跳到\((i,j)\)的方案数，那么不难得到如下转移

\[f[i][j]=\sum\limits_{k=1}^{\frac n2}f[i-2k+1][j-1]+f[i-2k+1][j]+f[i-2k+1][j+1]
\]

然后维护两个前缀和\(s1,s2\)，分别表示与当前列相差为偶数的前缀和以及与当前列相差为奇数的前缀和，那么可以这样转移

\[s1[i+1][j]=s2[i][j]+s1[i][j-1]+s1[i][j]+s1[i][j+1]
\]

\[s2[i+1][j]=s1[i][j]
\]

然而直接转移会T，我们考虑用矩阵乘法来优化。构造一个\(1*2n\)的矩阵表示答案，左边表示\(f[i]\)，右边表示\(f[i-1]\)，那么要构造一个\(2n*2n\)的转移矩阵满足乘上之后左边变为\(f[i+1]\)，右边为\(f[i]\)，那么大概是这么个东西（\(n=5\)的情况，图片网上偷的）

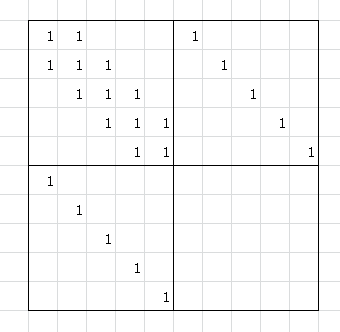
然后最后前缀和减一减就好了

//minamoto
#include<bits/stdc++.h>
#define R register int
#define fp(i,a,b) for(R i=a,T=b+1;i<T;++i)
#define fd(i,a,b) for(R i=a,T=b-1;i>T;--i)
using namespace std;
const int P=30011;
int n,m;
struct node{
    int a[105][105];
    node(){memset(a,0,sizeof(a));}
    int *operator [](const R &x){return a[x];}
    node operator *(node &b){
        node res;
        fp(i,1,n)fp(j,1,n)fp(k,1,n)
        res[i][j]=(res[i][j]+a[i][k]*b[k][j])%P;
        return res;
    }
}I,A,B;
node ksm(node x,R y){
    node res;fp(i,1,n)res[i][i]=1;
    for(;y;y>>=1,x=x*x)if(y&1)res=res*x;
    return res;
}
int main(){
//	freopen("testdata.in","r",stdin);
    scanf("%d%d",&n,&m);
    fp(i,1,n)I[i][i]=I[i+n][i]=I[i][i+n]=1;
    fp(i,1,n-1)I[i+1][i]=I[i][i+1]=1;
    n<<=1,A=ksm(I,m-2),B=A*I;
    printf("%d\n",(B[1][n>>1]-A[1][n]+P)%P);
    return 0;
}