模拟退火算法（西安网选赛hdu5017）

Ellipsoid

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Total Submission(s): 648    Accepted Submission(s): 194

Special Judge

Problem Description

Given a 3-dimension ellipsoid(椭球面)




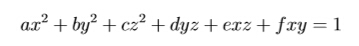
your task is to find the minimal distance between the original point (0,0,0) and points on the ellipsoid. The distance between two points (x₁,y₁,z₁) and (x₂,y₂,z₂) is defined as

 

Input

There are multiple test cases. Please process till EOF.



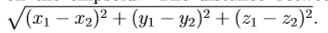
For each testcase, one line contains 6 real number a,b,c(0 < a,b,c,< 1),d,e,f(0 ≤ d,e,f < 1), as described above.It is guaranteed that the input data forms a ellipsoid. All numbers are fit in double.

 

Output

For each test contains one line. Describes the minimal distance. Answer will be considered as correct if their absolute error is less than 10^-5.

 

Sample Input

1 0.04 0.01 0 0 0

 

Sample Output

1.0000000
模拟退火算法：（Simulated Annealing，简称SA）是一种通用概率算法，用来在一个大的搜寻空间内找寻命题的最优解。
设：Y（x）是功能函数；要求最大值，x[i+1]是x[i]的下一个点，若Y(x[i+1])>=Y(x[i])，移动后可以得到更优解，总是接收移动；
若Y(x[i+1])<Y(x[i])(即移动后的解比当前解要差)，则以一定的概率接受移动，而且这个概率随着时间推移逐渐降低（逐渐降低才能趋向稳定）

下面给出模拟退火的伪代码：

/*
* J(y)：在状态y时的评价函数值
* Y(i)：表示当前状态
* Y(i+1)：表示新的状态
* r： 用于控制降温的快慢
* T： 系统的温度，系统初始应该要处于一个高温的状态
* T_min ：温度的下限，若温度T达到T_min，则停止搜索
*/
while( T > T_min )
{
　　dE = J( Y(i+1) ) - J( Y(i) ) ; 

　　if ( dE >=0 ) //表达移动后得到更优解，则总是接受移动
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
　　else
　　{
// 函数exp( dE/T )的取值范围是(0,1) ，dE/T越大，则exp( dE/T )也
if ( exp( dE/T ) > random( 0 , 1 ) )
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
　　}
　　T = r * T ; //降温退火 ，0<r<1 。r越大，降温越慢；r越小，降温越快
　　/*
　　* 若r过大，则搜索到全局最优解的可能会较高，但搜索的过程也就较长。若r过小，则搜索的过程会很快，但最终可能会达到一个局部最优值
　　*/
　　i ++ ;
}

程序：

#include"string.h"
#include"stdio.h"
#include"queue"
#include"stack"
#include"vector"
#include"algorithm"
#include"iostream"
#include"math.h"
#include"stdlib.h"
#define M 100009
#define inf 100000
#define eps 1e-10
#define PI acos(-1.0)
using namespace std;
int disx[9]={0,0,1,-1,1,-1,1,-1};
int disy[9]={1,-1,0,0,1,1,-1,-1};
double a,b,c,d,e,f;
double fun(double x,double y,double z)
{
    return sqrt(x*x+y*y+z*z);
}
double cal(double x,double y)
{
    double A=c;
    double B=d*y+e*x;
    double C=f*x*y+a*x*x+b*y*y-1;
    double ff=B*B-4*A*C;
    if(ff<0.0)return inf*100;
    ff=sqrt(ff);
    double z1=(-B+ff)/(2*A);
    double z2=(-B-ff)/(2*A);
    if(fun(x,y,z1)<fun(x,y,z2))
        return z1;
    return z2;
}
double solve()
{
    double x=0,y=0,z=sqrt(1/c);
    double step=1,rate=0.99;
    while(step>eps)
    {
        for(int i=0;i<8;i++)
        {
            double xx=x+step*disx[i];
            double yy=y+step*disy[i];
            double zz=cal(xx,yy);
            if(zz>=inf*99)continue;
            if(fun(xx,yy,zz)<fun(x,y,z))
            {
                x=xx;
                y=yy;
                z=zz;
            }
        }
        step*=rate;
    }
    return fun(x,y,z);
}
int main()
{
    while(scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e,&f)!=-1)
    {
        double ans=solve();
        printf("%.7lf\n",ans);
    }
    return 0;
}