[BZOJ 1177] Oil

Link:https://www.lydsy.com/JudgeOnline/problem.php?id=1177

Solution:

相当于将大矩形分为3块，取每块中最大的正方形

对于此类分成几块的题目，要想到枚举分割线

一共只有这6种情况：

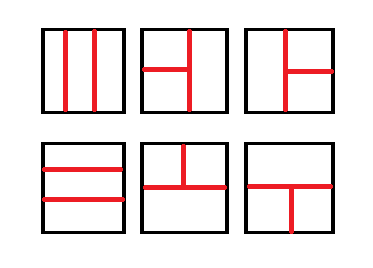
我们只要先预处理左上左下右上右下四个方向最大答案的前缀和，

再对于每种情况枚举分割线即可

对于最左边的两种情况，只要将中间一列的宽度保证为k即可

Code:

#include <bits/stdc++.h>

using namespace std;
const int MAXN=+;

int n,m,k,t,res=,s[MAXN][MAXN],a[MAXN][MAXN],b[MAXN][MAXN],c[MAXN][MAXN],d[MAXN][MAXN];

int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(int i=;i<=n;i++)
        for(int j=;j<=m;j++)
            scanf("%d",&t),s[i][j]=s[i-][j]+s[i][j-]-s[i-][j-]+t;
    for(int i=n;i>=k;i--) for(int j=m;j>=k;j--) s[i][j]-=s[i-k][j]+s[i][j-k]-s[i-k][j-k];

    for(int i=k;i<=n;i++) for(int j=k;j<=m;j++) a[i][j]=max(s[i][j],max(a[i-][j],a[i][j-]));
    for(int i=k;i<=n;i++) for(int j=m-k+;j>=;j--) b[i][j]=max(s[i][j+k-],max(b[i-][j],b[i][j+]));
    for(int i=n-k+;i>=;i--) for(int j=k;j<=m;j++) c[i][j]=max(s[i+k-][j],max(c[i+][j],c[i][j-]));
    for(int i=n-k+;i>=;i--) for(int j=m-k+;j>=;j--) d[i][j]=max(s[i+k-][j+k-],max(d[i+][j],d[i][j+]));

    for(int i=k;i<=n;i++) for(int j=k;j<=m;j++) res=max(res,a[i][j]+b[i][j+]+c[i+][m]);
    for(int i=n-k+;i>=;i--) for(int j=k;j<=m;j++) res=max(res,c[i][j]+d[i][j+]+a[i-][m]);
    for(int i=k;i<=n;i++) for(int j=k;j<=m;j++) res=max(res,a[i][j]+c[i+][j]+d[][j+]);
    for(int i=k;i<=n;i++) for(int j=m-k+;j>=;j--) res=max(res,b[i][j]+d[i+][j]+c[][j-]);

    for(int i=*k;i<=n;i++) for(int j=k;j<=m;j++) res=max(res,s[i][j]+a[i-k][m]+c[i+][m]);
    for(int j=*k;j<=m;j++) for(int i=k;i<=n;i++) res=max(res,s[i][j]+a[n][j-k]+b[n][j+]);

    printf("%d",res);
    return ;
}

Review:

由求三块权值和最大的不交叉的正方形  ------->  将矩形分为3块  -------->  枚举分割线

碰到求不相交的最值问题时，想到切割+枚举切割线的方法