广度优先搜索（BFS）思路及算法分析

1、算法用途：

是一种图像搜索演算法。用于遍历图中的节点，有些类似于树的深度优先遍历。这里唯一的问题是，与树不同，图形可能包含循环，因此我们可能会再次来到同一节点。

2、主要思想：

主要借助一个队列、一个布尔类型数组、邻接矩阵完成（判断一个点是否查看过，用于避免重复到达同一个点，造成死循环等），先将各点以及各点的关系存入邻接矩阵。

再从第一个点开始，将一个点存入队列，然后在邻接表中找到他的相邻点，存入队列，每次pop出队列头部并将其打印出来（文字有些抽象，实际过程很简单），整个过程有点像往水中投入石子水花散开。

 

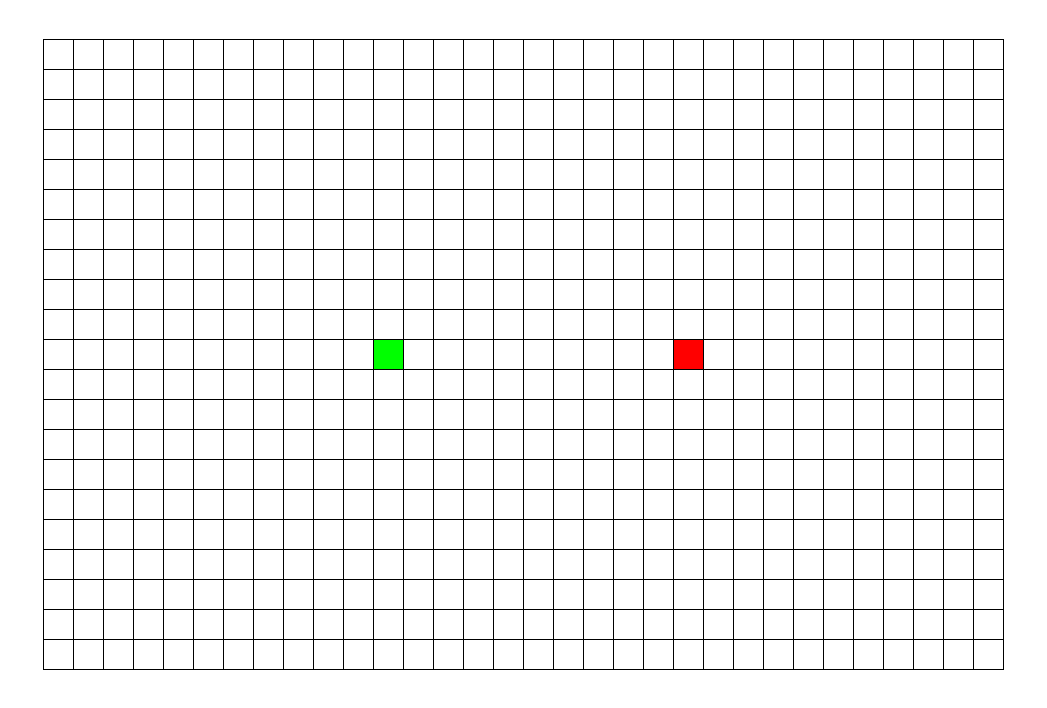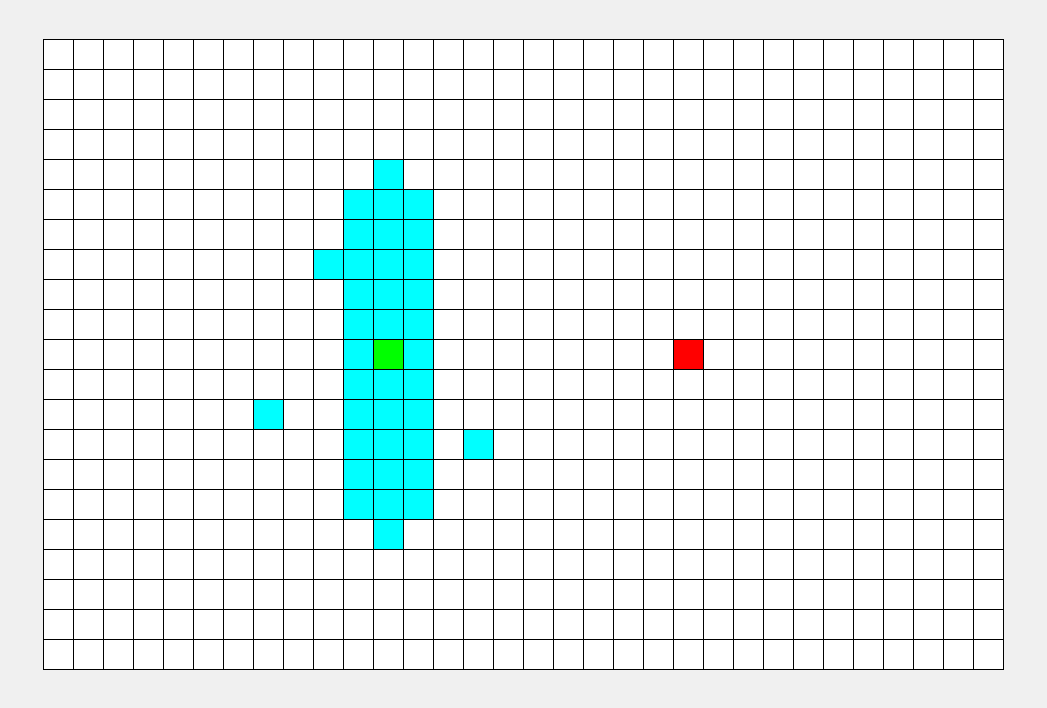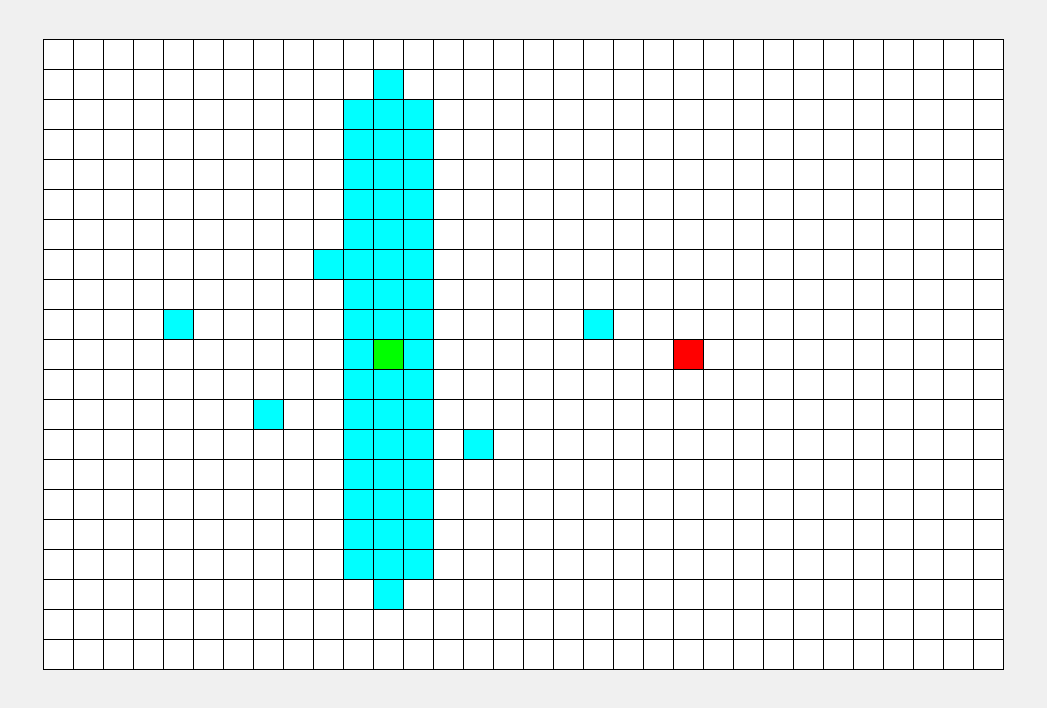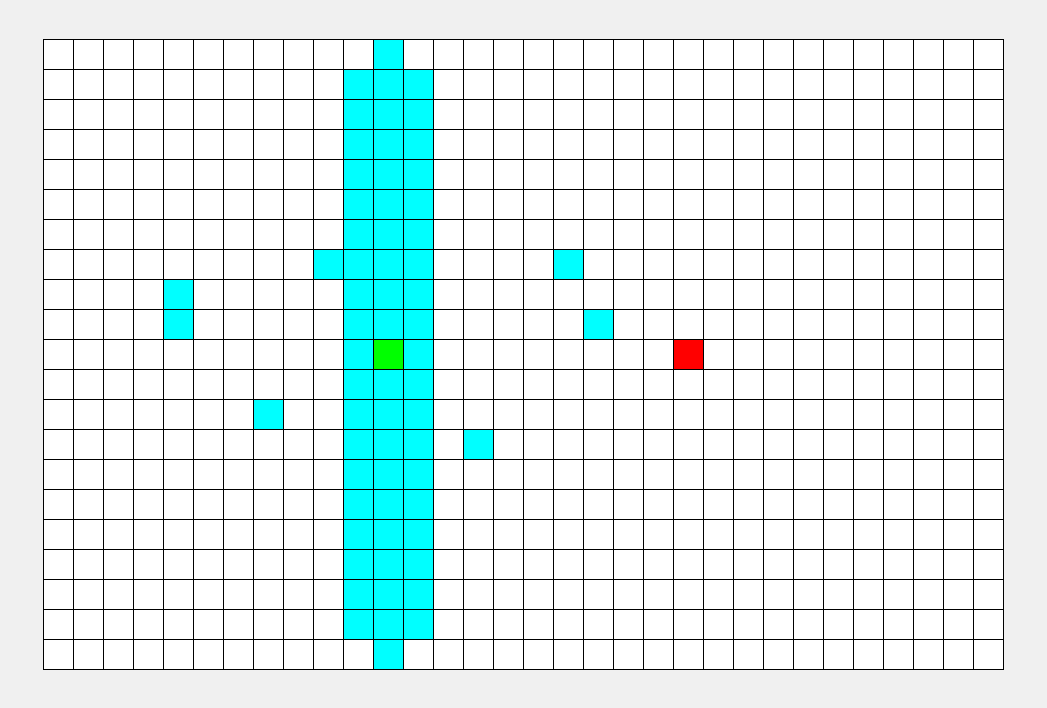
（邻接表是表示了图中与每一个顶点相邻的边集的集合，这里的集合指的是无序集）

3、代码（java）：

(以上图为例的代码）

 import java.util.*;

 //This class represents a directed graph using adjacency list
 //representation
 class Graph1 {
     private static int V; // No. of vertices
     private LinkedList<Integer> adj[]; // Adjacency Lists

     // Constructor
     Graph1(int v) {
         V = v;
         adj = new LinkedList[v];
         for (int i = 0; i < v; ++i)
             adj[i] = new LinkedList();
     }

     // Function to add an edge into the graph
     void addEdge(int v, int w) {
         adj[v].add(w);
     }

     // prints BFS traversal from a given source s
     public void BFS() {
         // Mark all the vertices as not visited(By default
         // set as false)
         boolean visited[] = new boolean[V];
         // Create a queue for BFS
         LinkedList<Integer> queue = new LinkedList<Integer>();

         for (int i = 0; i < V; i++) {
             if (!visited[i]) {
                 BFSUtil(i, visited, queue);
             }
         }
     }

     public void BFSUtil(int s, boolean visited[], LinkedList<Integer> queue) {
         // Mark the current node as visited and enqueue it
         visited[s] = true;
         queue.add(s);

         while (queue.size() != 0) {
             // Dequeue a vertex from queue and print it
             s = queue.poll();
             System.out.print(s + " ");

             // Get all adjacent vertices of the dequeued vertex s
             // If a adjacent has not been visited, then mark it
             // visited and enqueue it
             Iterator<Integer> i = adj[s].listIterator();
             while (i.hasNext()) {
                 int n = i.next();
                 if (!visited[n]) {
                     visited[n] = true;
                     queue.add(n);
                 }
             }
         }
     }

     // Driver method to
     public static void main(String args[]) {
         Graph1 g = new Graph1(4);

         g.addEdge(0, 1);
         g.addEdge(0, 2);
         g.addEdge(1, 2);
         g.addEdge(2, 0);
         g.addEdge(2, 3);
         g.addEdge(3, 3);

         System.out.println("Following is Breadth First Traversal " + "(starting from vertex 2)");
         g.BFS();
     }
 }

4、复杂度分析：

算法借助了一个邻接表和队列，故它的空问复杂度为O(V）。 遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间取决于所采用结构。 邻接表表示时，查找所有顶点的邻接点所需时间为O(E)，访问顶点的邻接点所花时间为O（V）,此时，总的时间复杂度为O(V+E)。