后序线索化二叉树（Java版）

前面介绍了前序线索化二叉树、中序线索化二叉树，本文将介绍后序线索化二叉树。之所以用单独的一篇文章来分析后序线索化二叉树，是因为后序线索化二叉树比前序、中序要复杂一些；另外在复习线索化二叉树的过程中，大部分讲解数据结构的书籍中都是以中序线索化为例，在网上搜索也很少有详细讲解前序、后序线索化的文章，对于使用Java语言编写的代码更是凤毛麟角，因此决定把个人的理解过程记录下，并分享给有需要的同学参考。

一、图解后序线索化

如果你很清楚的理解了前序、中序线索化二叉树，那么下面的图解不难理解；如果你还未掌握前序、中序线索化二叉树，请先详细了解线索二叉树之前序、中序线索化，然后再回来阅读本文更便于理解。 

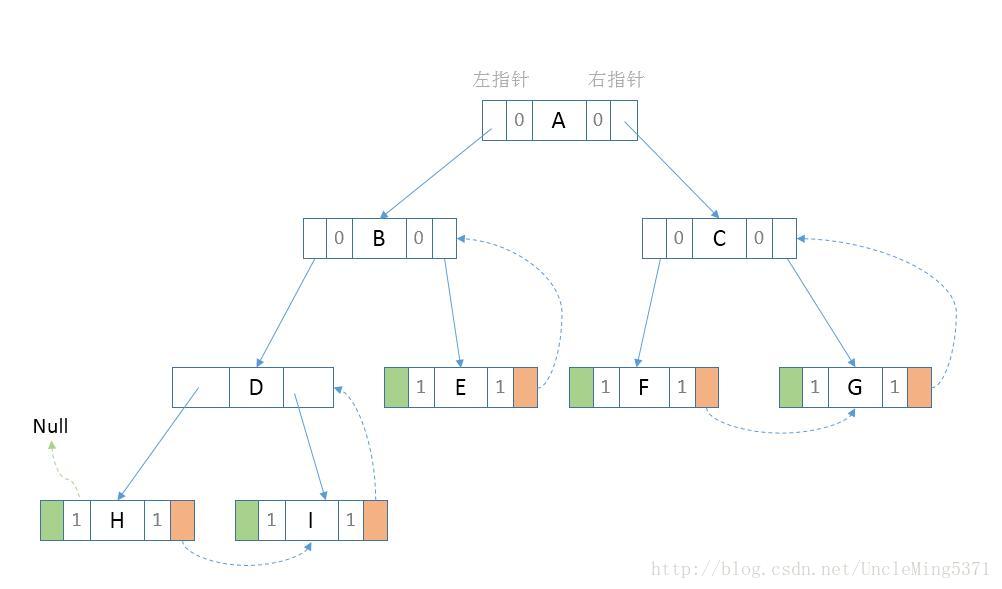
      下图是一棵后序线索化的二叉树，如下图：

为了更清晰、直观的表示出后继线索，在上图中忽略了前驱线索，请自行脑补。通过观察上图，节点H的后继节点是I，因此节点H的right指针指向I；节点I的后继节点是D，因此节点D的right指针指向D；节点D的后继节点是E，但是节点D的right指针指向了子节点B，因此D的right指针也就不能指向后继节点；同理节点B也没办法指向后继节点F。 

      对这棵二叉树完成后序线索化之后，我们在对其进行遍历时，我们知道后序遍历的顺序是：左右根，那对于上图的后序遍历结果是：HIDEBFGCA。

      遍历后序线索化二叉树的思路：由于是后序线索化，那么后序遍历的开始节点一定是最左子节点，从根节点出发找到最左子节点，如何判断是否是最左子节点呢？如果是最左子节点，则其left指针一定的线索，如上图我们找到最左子节点H，H的right指针是后继线索，找到节点I，节点I的right指针是后继线索，找到节点D，节点D的right指针是子节点I，并不是后继线索指针，那么问题来了？此时我们该如何处理呢？

通过观察D的后继节点E，但是D与E没有直接线索，不过D的父节点是B，B的右字节是E，存在这样一个间接的关系，我们是否可以利用这个间接的关系呢？答案是肯定的，但是按照我们上文介绍的节点数据结构，并不存在指向父节点的指针，因此我们要对节点数据结构进行修改，修改如下：

//节点存储结构
static class Node {
    String data;        //数据域
    Node left;          //左指针域
    Node right;         //右指针域
    Node parent;        //父节点的指针（为了后序线索化使用）
    boolean isLeftThread = false;   //左指针域类型  false：指向子节点、true：前驱或后继线索
    boolean isRightThread = false;  //右指针域类型  false：指向子节点、true：前驱或后继线索

    Node(String data) {
        this.data = data;
    }
}

按照如上的存储结构增加了parent指针之后，D节点存在了指向父节点B的指针。当遍历到D节点时找到D节点的父节点B，B的right指针指向了子节点E，E的right指针又指向了B，这里又出现了另一个问题，就是进入了两次B，如果按照前面的方式则进入了一个死循环。以节点B为例，我们什么时候去找B的父节点，什么时候去处理他的右节点呢。我们分析下两次进入节点B，第一次是通过B的左节点进入，第二次是通过右子节点进入，我们可以记录上一个处理的节点，如果上一个处理的节点是B的左节点，则接下进入B的右节点，如果上一个处理的节点是B的右节点，则说明B的左右子树都处理完成，继续处理B的父节点。

二、Java代码实现后序线索化

package com.bj58.demo.struct;

/**
 * @Title: 后序线索化二叉树相关操作
 * @Description：
 * @Author： Uncle Ming
 * @Date：2017年1月8日 下午3:42:14
 * @Version V1.0
 */
public class PostThreadBinaryTree {

    private Node preNode;   //线索化时记录前一个节点

    //节点存储结构
    static class Node {
        String data;        //数据域
        Node left;          //左指针域
        Node right;         //右指针域
        Node parent;        //父节点的指针（为了后序线索化使用）
        boolean isLeftThread = false;   //左指针域类型  false：指向子节点、true：前驱或后继线索
        boolean isRightThread = false;  //右指针域类型  false：指向子节点、true：前驱或后继线索

        Node(String data) {
            this.data = data;
        }
    }

    /**
     * 通过数组构造一个二叉树（完全二叉树）
     * @param array
     * @param index
     * @return
     */
    static Node createBinaryTree(String[] array, int index) {
        Node node = null;

        if(index < array.length) {
            node = new Node(array[index]);
            node.left = createBinaryTree(array, index * 2 + 1);
            node.right = createBinaryTree(array, index * 2 + 2);

            //记录节点的父节点（后序线索化遍历时使用）
            if(node.left != null) {
                node.left.parent = node;
            }

            if(node.right != null) {
                node.right.parent = node;
            }
        }

        return node;
    }

    /**
     * 后序线索化二叉树
     * @param node  节点
     */
    void postThreadOrder(Node node) {
        if(node == null) {
            return;
        }

        //处理左子树
        postThreadOrder(node.left);
        //处理右子树
        postThreadOrder(node.right);

        //左指针为空,将左指针指向前驱节点
        if(node.left == null) {
            node.left = preNode;
            node.isLeftThread = true;
        }

        //前一个节点的后继节点指向当前节点
        if(preNode != null && preNode.right == null) {
            preNode.right = node;
            preNode.isRightThread = true;
        }
        preNode = node;
    }

    /**
     * 后续遍历线索二叉树，按照后继方式遍历（思路：后序遍历开始节点是最左节点）
     * @param node
     */
    void postThreadList(Node root) {
        //1、找后序遍历方式开始的节点
        Node node = root;
        while(node != null && !node.isLeftThread) {
            node = node.left;
        }

        Node preNode = null;
        while(node != null) {
            //右节点是线索
            if(node.isRightThread) {
                System.out.print(node.data + ", ");
                preNode = node;
                node = node.right;

            } else {
                //如果上个处理的节点是当前节点的右节点
                if(node.right == preNode) {
                    System.out.print(node.data + ", ");
                    if(node == root) {
                        return;
                    }

                    preNode = node;
                    node = node.parent;

                } else {    //如果从左节点的进入则找到有子树的最左节点
                    node = node.right;
                    while(node != null && !node.isLeftThread) {
                        node = node.left;
                    }
                }
            }
        }
    }

    public static void main(String[] args) {
        String[] array = {"A", "B", "C", "D", "E", "F", "G", "H", "I"};
        Node root = createBinaryTree(array, 0);

        PostThreadBinaryTree tree = new PostThreadBinaryTree();
        tree.postThreadOrder(root);
        System.out.println("后序按后继节点遍历线索二叉树结果：");
        tree.postThreadList(root);
    }
}

运行结果如下：

后序按后继节点遍历线索二叉树结果：
H, I, D, E, B, F, G, C, A, 

三、前序、中序、后序线索化比较

1. 前序线索化二叉树遍历相对最容易理解，实现起来也比较简单。由于前序遍历的顺序是：根左右，所以从根节点开始，沿着左子树进行处理，当子节点的left指针类型是线索时，说明到了最左子节点，然后处理子节点的right指针指向的节点，可能是右子树，也可能是后继节点，无论是哪种类型继续按照上面的方式（先沿着左子树处理，找到子树的最左子节点，然后处理right指针指向），以此类推，直到节点的right指针为空，说明是最后一个，遍历完成。 

2. 中序线索化二叉树的网上相关介绍最多。中序遍历的顺序是：左根右，因此第一个节点一定是最左子节点，先找到最左子节点，依次沿着right指针指向进行处理（无论是指向子节点还是指向后继节点），直到节点的right指针为空，说明是最后一个，遍历完成。 

3. 后序遍历线索化二叉树最为复杂，通用的二叉树数节点存储结构不能够满足后序线索化，因此我们扩展了节点的数据结构，增加了父节点的指针。后序的遍历顺序是：左右根，先找到最左子节点，沿着right后继指针处理，当right不是后继指针时，并且上一个处理节点是当前节点的右节点，则处理当前节点的右子树，遍历终止条件是：当前节点是root节点，并且上一个处理的节点是root的right节点。

转载自：https://blog.csdn.net/UncleMing5371/article/details/54291221