力扣441(java&python)-排列硬币（简单）

题目：

你总共有 n 枚硬币，并计划将它们按阶梯状排列。对于一个由 k 行组成的阶梯，其第 i 行必须正好有 i 枚硬币。阶梯的最后一行 可能 是不完整的。

给你一个数字 n ，计算并返回可形成 完整阶梯行 的总行数。

示例 1：

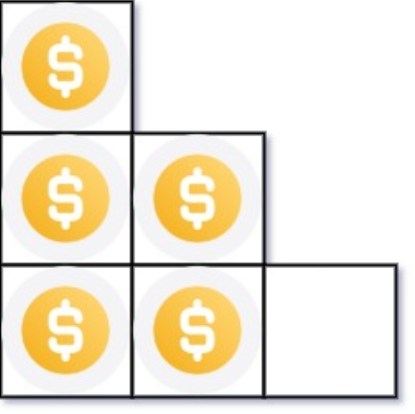
输入：n = 5

输出：2

解释：因为第三行不完整，所以返回 2 。

示例 2：

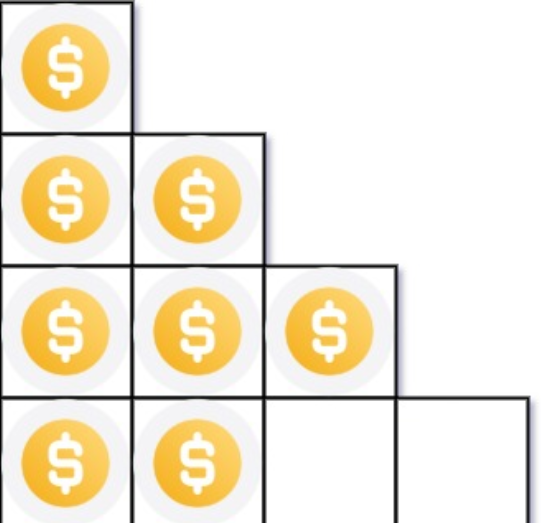
输入：n = 8

输出：3

解释：因为第四行不完整，所以返回 3 。

提示：

• 1 <= n <= 2^31 - 1

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/arranging-coins
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

【二分查找】

1.初始化left = 1, right = n，计算出mid = left + (right - left + 1) / 2，等差数列的前n项和公式：sum =  n * (n + 1) / 2（首项和公差都为1），计算出包括mid项以及之前的和；

2.循环条件：left < right：

• sum <= n 时，说明mid以及mid以后的数可能为答案，即缩小搜索区间为：[mid, right]（注意这里区间的死循环哦！故mid才向上取整）;
• sum > n 时，说明mid之前的数才可能为答案，即缩小搜索区间为：[left, mid-1];

3.循环结束的条件： left == right，区间缩小为一个点，故返回left 或者right都可以。

java代码：

 1 class Solution {
 2     public int arrangeCoins(int n) {
 3         int left = 1, right = n;
 4         while (left < right){
 5             int mid = left + (right - left + 1) / 2;
 6             long sum = (long) mid * (mid + 1) / 2;
 7             //区间为：[mid, right]
 8             if(sum <= n){
 9                 left = mid;
10             }else {
11                 //区间为：[left, mid - 1]
12                 right = mid - 1;
13             }
14         }
15         return left;
16     }
17 }

python3代码：

 1 class Solution:
 2     def arrangeCoins(self, n: int) -> int:
 3         left, right = 1, n
 4         while left <= right:
 5             mid = left + (right - left) // 2
 6             sum = mid * (mid + 1) // 2
 7             if sum < n:
 8                 left = mid + 1
 9             elif sum > n:
10                 right = mid - 1
11             else:
12                 return mid
13         # 循环结束，left比right大1，找小的那个
14         return right

 【数学方法】：

等差数列的前n项和公式：sum =  x * (x + 1) / 2（首项和公差都为1）,这里需要求 x * (x + 1) / 2 < = n，求得x的最大值，解一元二次不等式：得到关于x的不等式为：

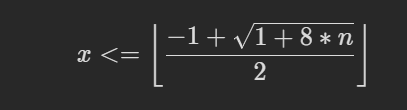
 java代码为：

1 class Solution {
2     public int arrangeCoins(int n) {
3      return (int)((Math.sqrt(1 + (long)8 * n) - 1) / 2);
4     }
5 }