XGBooost算法原理及Python实现

一、概述

XGBoost 是一种基于梯度提升框架的机器学习算法，它通过迭代地训练一系列决策树来构建模型。核心思想是通过不断地在已有模型的基础上，拟合负梯度方向的残差（真实值与预测值的差）来构建新的弱学习器，达到逐步优化模型的目的。

XGBoost 在构建决策树时，利用了二阶导数信息。在损失函数的优化过程中，不仅考虑了一阶导数（梯度），还引入了二阶导数（海森矩阵），这使得算法能够更精确地找到损失函数的最优解，加速模型的收敛速度，同时提高模型的泛化能力。此外，XGBoost 还加入了正则化项，包括 L1 和 L2 正则化，用于控制模型的复杂度，防止过拟合。

二、算法原理

1.算法过程

在 XGBoost 中，弱学习器通常是 CART（分类与回归树）决策树。每一棵决策树的构建都是基于前一轮模型的预测结果与真实值之间的残差。具体过程为：

(1) 初始化模型

首先，初始化一个简单的模型，通常是一个常数模型，记为$f_0(X)$ ，其预测值为所有样本真实值的均值（回归任务）或多数类（分类任务），记为$\hat y_0$。此时，模型的预测结果与真实值之间存在误差。

(2) 计算残差或负梯度

在回归任务中，计算每个样本的残差，即真实值$y_i$与当前模型预测值$\hat y_{i,t-1}$的差值$r_{i,t}=y_i-\hat y_{i,t-1}$，其中表示迭代的轮数。在分类任务中，计算损失函数关于当前模型预测值的负梯度$$g_{i,t}=-\frac{\vartheta L(y_i,\hat y_{i,t-1})}{\vartheta \hat y_{i,t-1}}$$

(3) 拟合决策树

使用计算得到的残差（回归任务）或负梯度（分类任务）作为新的目标值，训练一棵新的决策树$f_t(X)$。这棵树旨在拟合当前模型的误差，从而弥补当前模型的不足。

(4) 更新模型

根据新训练的决策树，更新当前模型。更新公式为$\hat y_{i,t}=\hat y_{i,t-1}+\alpha f_t(x_i)$，其中是学习率（也称为步长），用于控制每棵树对模型更新的贡献程度。学习率较小可以使模型训练更加稳定，但需要更多的迭代次数；学习率较大则可能导致模型收敛过快，甚至无法收敛。

(5) 重复迭代

重复步骤 (2)–(4)步，不断训练新的决策树并更新模型，直到达到预设的迭代次数、损失函数收敛到一定程度或满足其他停止条件为止。最终，XGBoost由多棵决策树组成，其预测结果是所有决策树预测结果的累加。

算法过程图示

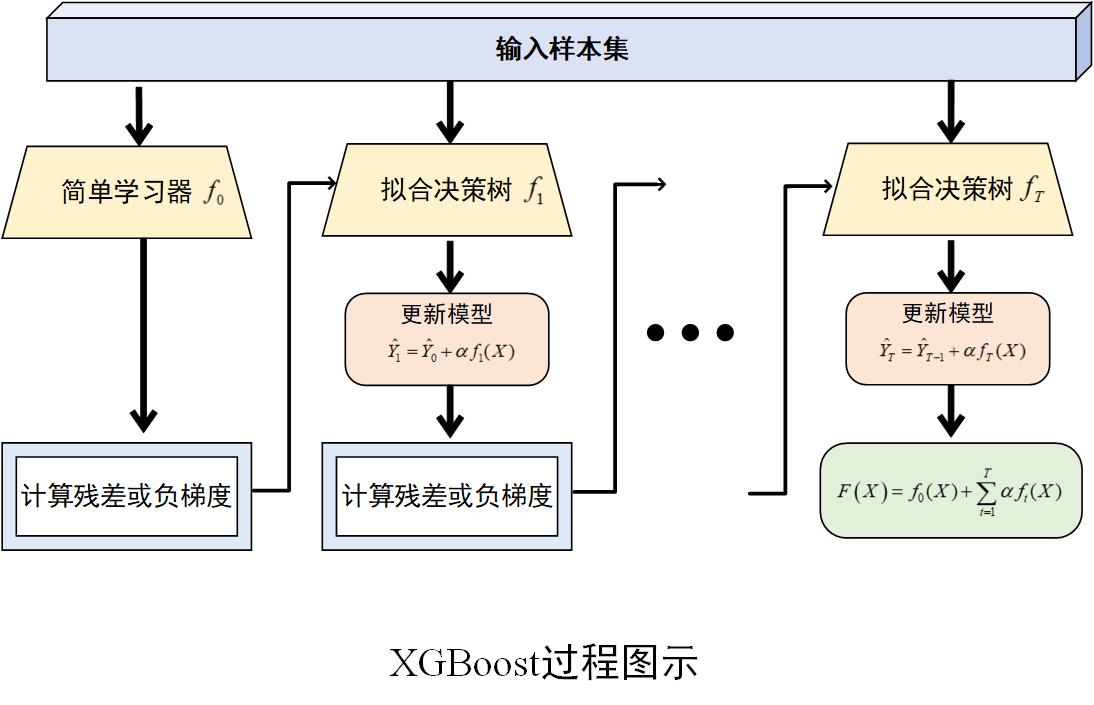
2.目标函数优化

XGBoost 通过定义一个目标函数来衡量模型的优劣，并在每次迭代中优化这个目标函数。目标函数包括损失函数和正则化项两部分：

损失函数：用于衡量模型预测值与真实值之间的差异，常见的损失函数有均方误差（MSE，用于回归问题）、交叉熵损失（用于分类问题）等。损失函数反映了模型对训练数据的拟合程度。

正则化项：为了防止模型过拟合，XGBoost 在目标函数中加入了正则化项。正则化项通常基于决策树的复杂度，例如树的叶子节点数量、叶子节点权重的 L1 或 L2 范数等。正则化项对模型的复杂度进行惩罚，使得模型在拟合数据的同时保持简单，从而提高模型的泛化能力。

在每次迭代中，XGBoost 通过贪心算法寻找最优的分裂点，使得目标函数在该次迭代中下降最多。具体来说，它会遍历所有可能的特征和分裂点，计算每个分裂点对目标函数的影响，选择使目标函数下降最大的分裂点作为当前节点的分裂点。

三、与GBDT的区别

算法原理

GDBT：是基于决策树的集成学习算法，通过不断生成新的决策树来拟合之前模型的残差，从而逐步提升模型的准确性。

XGBoost：在 GDBT 的基础上进行了优化和扩展，不仅可以拟合残差，还引入了二阶导数信息来更准确地逼近目标函数，从而提高模型的精度。

目标函数

GDBT：通常使用经验风险最小化作为目标，例如均方误差（MSE）、对数损失等，通过迭代优化目标函数来构建模型。

XGBoost：目标函数在经验风险的基础上，增加了正则化项，用于控制模型的复杂度，防止过拟合，使得模型具有更好的泛化能力。

决策树生成

GDBT：决策树的生成过程是基于贪心算法，在每个节点上选择能够最大程度降低损失函数的特征和分裂点。

XGBoost：在决策树生成时，除了考虑特征和分裂点对损失函数的影响外，还考虑了数据的稀疏性、特征的重要性等因素，采用了更复杂的分裂策略，能够更高效地处理大规模数据和高维数据。

并行计算

GDBT：一般情况下，GDBT 算法是顺序生成决策树的，难以进行并行计算，训练速度相对较慢。

XGBoost：支持分布式和并行计算，可以利用多线程、多节点来加速模型的训练过程，大大提高了训练效率，尤其适用于大规模数据集。

对缺失值的处理

GDBT：通常需要对缺失值进行填充或者单独处理，否则在计算分裂点时可能会出现问题。

XGBoost：能够自动学习缺失值的处理方式，在决策树分裂时，会同时考虑将缺失值划分到左子树和右子树的情况，选择最优的划分方式，对缺失值的鲁棒性更强。

四、Python实现

（环境： Python 3.11，scikit-learn 1.6.1）

（1）分类情形

from sklearn.datasets import make_classification

from sklearn.model_selection import train_test_split

import xgboost as xgb

from sklearn import metrics

# 生成数据集

X, y = make_classification(n_samples = 1000, n_features = 6, random_state = 42)

# 将数据集划分为训练集和测试集

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)

# 创建XGBoost分类模型

clf = xgb.XGBClassifier()

# 训练模型

rclf = clf.fit(X_train, y_train)

# 预测

y_pre = rclf.predict(X_test)

# 性能评价

accuracy = metrics.accuracy_score(y_test,y_pre)

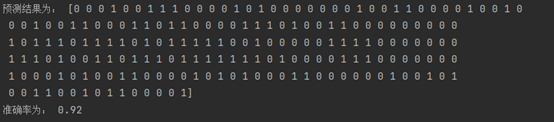
print('预测结果为：',y_pre)

print('准确率为：',accuracy)

（2）回归情形

from sklearn.datasets import make_regression

from sklearn.model_selection import train_test_split

import xgboost as xgb

from sklearn.metrics import mean_squared_error

# 生成回归数据集

X, y = make_regression(n_samples = 1000, n_features = 6, random_state = 42)

# 将数据集划分为训练集和测试集

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)

# 创建XGBoost回归模型

model = xgb.XGBRegressor(n_estimators = 100, learning_rate = 0.1, max_depth = 3)

# 训练模型

model.fit(X_train, y_train)

# 进行预测

y_pred = model.predict(X_test)

# 计算均方误差评估模型性能

mse = mean_squared_error(y_test, y_pred)

print(f"均方误差: {mse}")

End.

下载