NOIP2023模拟9联测30 T4 金牌

LCA 还能 $O(1)$……

思路

思路非常简单，可考试就是想歪成统计指数了……

将一条穿过 $(x,y)$ 的路径 $(u,v)$ 分为 $u \to x \to y \to v$，所以说对答案的贡献为：

\[2^{dis(u,x)+dis(x,y)+dis(y,v)}=2^{dis(u,x)}\times 2^{dis(x,y)}\times 2^{dis(y,v)}
\]

如果把 $(x,y)$ 的路径上的边断开，形成了若干联通块，设 $x$ 所在的联通块为 $E_x$，$y$ 所在的联通块为 $E_y$，答案为：

\[2^{dis(x,y)} {\sum_{i\in E_x} 2^{dis(i,x)}} \sum_{i=E_y} 2^{dis(y,i)}
\]

有了这个式子可以可以分类讨论求答案。

先以 1 为根建树。

若 u,v 的 lca 不是 u,v 中一点

可以通过 $sum_u=2\times\sum\limits_{v\in u.sons} sum_v$，预处理出子树 $u$ 内到 $u$ 的价值，$y$ 同理。

又可以通过 $dep_u+dep_v-2\times dep_{lca(u,v)}$ 求出 $u$ 和 $v$ 两点间的距离。（$dep$ 是以 1 为根时的深度）

代入公式即可求值。

若 u,v 的 lca 是 u,v 中一点

这样就比较复杂了，画一张图：

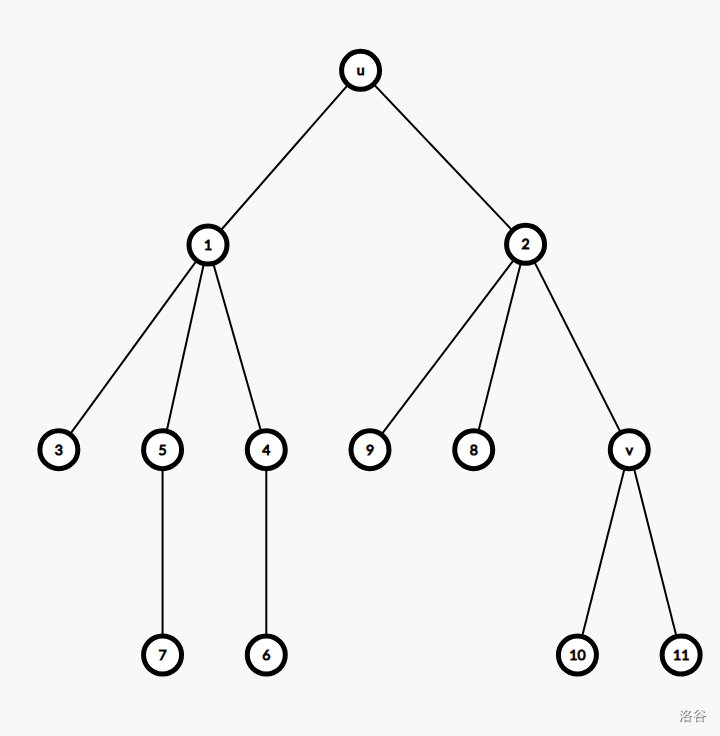
发现当 $u$ 为根时，答案就是 $v$ 子树内的距离和乘上距离的贡献再乘树$u$的距离和减去 $(u,v)$ 路径上 $u$ 的儿子子树内的距离和。

格式化就是 $(sum_u-sum_{u.son})\times 2^{dis(u,v)}\times sum_v$。

$u$ 做为根时 $u$ 的 $sum$ 可以换根 dp 快速求，$sum_v$ 和 $sum_{u.son}$ 可以直接用以 1 为根时求的 $sum$，距离可以用上述讨论的式子求。

$u.son$ 可以倍增时较深的节点先跳到较浅节点深度 $-1$ 的位置，查看如果此时较深节点的父亲是较浅的节点，就可以判断为这种情况，并且使 $u.son$ 等于当前较深节点。

CODE

文中使用倍增求 lca。

#include<bits/stdc++.h>

using namespace std;

#define ll long long

#define mod 998244353

#define S second

#define F first

const int maxn=2e6+5;

struct node

{

    int to,nxt;

}edge[maxn*2];

int n,tot;

int head[maxn],f[maxn][25],deep[maxn];

ll ans[maxn],sum[maxn];

vector< pair<int,int> >E[maxn];

ll ksm(ll x,ll y)

{

    ll sum=1;

    for(;y;y/=2,x=x*x%mod) if(y&1) sum=sum*x%mod;

    return sum;

}

void add(int x,int y)

{

    tot++;

    edge[tot].to=y;

    edge[tot].nxt=head[x];

    head[x]=tot;

}

void dfs(int u)

{

    sum[u]=1;

    for(int i=head[u];i;i=edge[i].nxt)

    {

        int v=edge[i].to;

        if(v==f[u][0]) continue;

        deep[v]=deep[u]+1;

        f[v][0]=u;

        for(int j=1;j<=20;j++) f[v][j]=f[f[v][j-1]][j-1];

        dfs(v);

        sum[u]=(sum[u]+sum[v]*2%mod)%mod;

    }

}

pair<int,int> Lca(int x,int y)

{

    if(deep[x]<deep[y]) swap(x,y);

    for(int i=20;i>=0;i--) if(deep[f[x][i]]>deep[y]) x=f[x][i];

    if(f[x][0]==y) return make_pair(f[x][0],x);//情况 2，返回 lca 和 u.son

    if(deep[x]>deep[y]) x=f[x][0];

    for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];

    return make_pair(f[x][0],0);

}

void dfs_hg(int u,ll dis)//换根 dp

{

    if(u!=1) dis=((dis-sum[u]*2%mod+mod)%mod*2%mod+sum[u])%mod;

    for(pair<int,int> v:E[u]) ans[v.S]=(ans[v.S]*((dis-sum[v.F]*2+mod)%mod))%mod;

    for(int i=head[u];i;i=edge[i].nxt)

    {

        int v=edge[i].to;

        if(v==f[u][0]) continue;

        dfs_hg(v,dis);

    }

}

int main()

{

    scanf("%d",&n);

    for(int i=1;i<n;i++)

    {

        int x,y;

        scanf("%d%d",&x,&y);

        add(x,y);

        add(y,x);

    }

    deep[1]=1;

    dfs(1);

    int m;

    scanf("%d",&m);

    for(int i=1;i<=m;i++)

    {

        int x,y;

        scanf("%d%d",&x,&y);

        pair<int,int> lca=Lca(x,y);//first 是 lca，seoncd 是 u.son

        if(lca.S)

        {

            E[lca.F].push_back(make_pair(lca.S,i));

            int k=x;

            if(lca.F==x) k=y;

            ans[i]=sum[k]*ksm(2,deep[x]+deep[y]-2*deep[lca.F])%mod;

        }

        else ans[i]=sum[x]*ksm(2,deep[x]+deep[y]-2*deep[lca.F])%mod*sum[y]%mod;

    }

    dfs_hg(1,sum[1]);

    for(int i=1;i<=m;i++) printf("%lld\n",(ans[i]+mod)%mod);

}

结束了吗？

尽管倍增和树剖的时间复杂度来到了优秀的 $O(\log n)$ 但这题卡常，我们不得不用 $O(1)$ 的预处理 lca。

啊这.jpg

lca 部分见博客预处理 O(1) 求 lca。（后面填）

在求 lca 的过程中，我们可以使用手写栈存下这一个节点的所有祖先，后面遍历虚边时，如果连接的点在栈中，那么 u.son 就等于栈中连接的点的下一个位置。

CODE

#include<bits/stdc++.h>

using namespace std;

#define ll long long

#define mod 998244353

#define S second

#define F first

#define ri register int

const int maxn=1e6+5;

struct node

{

    int to,nxt;

}edge[maxn*2];

int n,tot,tp;

int head[maxn],deep[maxn],x[maxn],y[maxn],vis[maxn],stk[maxn],fa[maxn];

ll ans[maxn],sum[maxn];

pair<int,int> Lca[maxn];

vector< pair<int,int> >E[maxn],EL[maxn];

inline int read() {

    int s = 0, w = 1;

    char ch = getchar();

    while (ch < '0' || ch > '9') {

        if (ch == '-')

            w = -1;

        ch = getchar();

    }

    while (ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();

    return s * w;

}

inline void write(ll X)

{

    if(X<0) {X=~(X-1); putchar('-');}

    if(X>9) write(X/10);

    putchar(X%10+'0');

}

inline ll ksm(ll x,ll y)

{

    ll sum=1;

    for(;y;y/=2,x=x*x%mod) if(y&1) sum=sum*x%mod;

    return sum;

}

inline void add(int x,int y)

{

    tot++;

    edge[tot].to=y;

    edge[tot].nxt=head[x];

    head[x]=tot;

}

inline int frt(int u)

{

    if(fa[u]==u) return u;

    return fa[u]=frt(fa[u]);

}

inline void dfs(int u)//O(1) lca

{

    stk[++tp]=u;

    vis[u]=tp;//u 节点在栈中的位置

    sum[u]=1;

    for(ri i=head[u];i;i=edge[i].nxt)

    {

        int v=edge[i].to;

        if(vis[v]) continue;

        deep[v]=deep[u]+1;

        dfs(v);

        fa[v]=u;

        sum[u]=(sum[u]+sum[v]*2%mod)%mod;

    }

    for(pair<int,int> i:EL[u])

    {

        if(vis[i.F]!=-1&&vis[i.F]!=0) Lca[i.S].S=stk[vis[i.F]+1];//如果栈，但没出栈，u.son 赋值

        else if(vis[i.F]) Lca[i.S].F=frt(i.F);

    }

    tp--;

    vis[u]=-1;//-1 表示入过栈，但已出栈

}

inline void dfs_hg(int u,ll dis,int f)

{

    if(u!=1) dis=((dis-sum[u]*2%mod+mod)%mod*2%mod+sum[u])%mod;

    for(pair<int,int> v:E[u]) ans[v.S]=(ans[v.S]*((dis-sum[v.F]*2+mod)%mod))%mod;

    for(ri i=head[u];i;i=edge[i].nxt)

    {

        int v=edge[i].to;

        if(v==f) continue;

        dfs_hg(v,dis,u);

    }

}

int main()

{

    n=read();

    for(ri i=1;i<n;i++)

    {

        int x,y;

        x=read(),y=read();

        add(x,y);

        add(y,x);

    }

    int m;

    m=read();

    for(ri i=1;i<=m;i++)

    {

        x[i]=read(),y[i]=read();

     	EL[x[i]].push_back(make_pair(y[i],i)),EL[y[i]].push_back(make_pair(x[i],i));//虚边

    }

    for(ri i=1;i<=n;i++) fa[i]=i;

    dfs(1);

    for(ri i=1;i<=m;i++)

    {

        pair<int,int> lca=Lca[i];

        if(lca.S)

        {

            E[lca.F].push_back(make_pair(lca.S,i));

            int k=x[i];

            if(lca.F==x[i]) k=y[i];

            ans[i]=sum[k]*ksm(2,deep[x[i]]+deep[y[i]]-2*deep[lca.F])%mod;

        }

        else ans[i]=sum[x[i]]*ksm(2,deep[x[i]]+deep[y[i]]-2*deep[lca.F])%mod*sum[y[i]]%mod;

    }

    dfs_hg(1,sum[1],0);

    for(ri i=1;i<=m;i++) write((ans[i]+mod)%mod),putchar('\n');

}