CF559E Gerald and Path 题解

CF559E Gerald and Path

很困难的 DP 题，状态不是很好想。对于这种线段覆盖类题目，显然先覆盖哪个线段没有影响，我们可以通过按照端点位置升序排序后按照顺序考虑，这样可能会有一些额外性质。

之后，考虑转移时需要什么东西来刻画一个状态的轮廓。显然我们需要知道现在是第几条线段，并且计算贡献需要知道覆盖右端点最远的线段以及其方向。如果这样设计状态，非最远线段的影响就会在加入最远线段时被计算，是正确的。

设状态 \(f_{i,j,k}\) 表示考虑到第 \(i\) 条线段，右端点最远的线段为 \(j\)，方向为 \(k\)。考虑刷表，枚举 \(p\) 为考虑到的线段，\(q\) 为其方向。我们可以在从小到大枚举 \(p\) 的时候顺便记录右端点最大的值 \(x\) 与此时的方向 \(y\)。

假设方向全都是向右，我们可以通过上图辅助理解。我们发现，增加的贡献可以分为两段。一段是 \(l+1\sim r\)，另一段是 \(r+1\sim mx\)。在此图中，第一段贡献为 \(r-l\)，第二段贡献是 \(mx-r\)，把这些加到转移时的贡献中。事实上，如果方向不是向右，也是一样的，

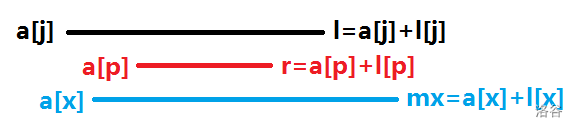
假设方向全都是向右，注意到还有这种情况。此时第二段贡献还是 \(mx-r\)，但是第一段贡献需要减去 \(l-r\)。注意到这等价于加上 \(r-l\)，所以维持原转移不变。

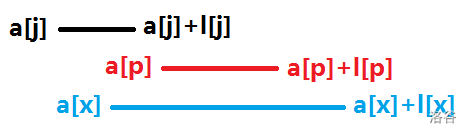
假设方向全都是向右，注意到还有这种情况。第二段贡献不变，但处理第一段时，如果 \(l\) 和 \(r\) 中间有空隙，那么 \(r-l\) 算出来的贡献就过大了，应该只有 \(l[p]\)。此时我们只需要把 \(r-l\) 和 \(l[p]\) 取较小值。

综上所述，状态转移方程为如下。

\[f_{p,x,y}=\max\{f_{p,x,y},f_{i,j,k}+\min\{l[p],r-l\}+mx-r\}
\]

时间复杂度 \(O(n^3)\)。

#include <bits/stdc++.h>
using namespace std;
struct val
{
	long long a,l;
}a[200];
long long n,f[200][200][2],ans=0;
bool cmp(struct val a,struct val b)
{
	return a.a<b.a;
}

int main()
{
	scanf("%lld",&n);
	for(int i=1;i<=n;i++)scanf("%lld%lld",&a[i].a,&a[i].l);
	sort(a+1,a+n+1,cmp);
	a[0].a=-1e18;
	for(int i=0;i<=n;i++)
	    for(int j=0;j<=i;j++)
	        for(int k=0;k<2;k++)
	            {
	            	long long l=a[j].a+k*a[j].l,mx=-1e18,x=0,y=0;
	            	for(int p=i+1;p<=n;p++)
	            	    for(int q=0;q<2;q++)
	            	        {
	            	        	long long r=a[p].a+q*a[p].l;
	            	        	if(r>mx)mx=r,x=p,y=q;
	            	        	f[p][x][y]=max(f[p][x][y],f[i][j][k]+min(a[p].l,r-l)+mx-r);
							}
				}
	for(int i=0;i<=n;i++)
	    for(int j=0;j<=i;j++)
	        for(int k=0;k<2;k++)
	            ans=max(ans,f[i][j][k]);
	printf("%lld\n",ans);
	return 0;
}