六、regularized logisitic regssion练习（转载）

转载链接：http://www.cnblogs.com/tornadomeet/archive/2013/03/17/2964858.html

在上一讲Deep learning：五(regularized线性回归练习)中已经介绍了regularization项在线性回归问题中的应用，这节主要是练习regularization项在logistic回归中的应用，并使用牛顿法来求解模型的参数。参考的网页资料为：http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex5/ex5.html。要解决的问题是，给出了具有2个特征的一堆训练数据集，从该数据的分布可以看出它们并不是非常线性可分的，因此很有必要用更高阶的特征来模拟。例如本程序中个就用到了特征值的6次方来求解。

　　实验基础：

　　contour:

　　该函数是绘制轮廓线的，比如程序中的contour(u, v, z, [0, 0], 'LineWidth', 2)，指的是在二维平面U-V中绘制曲面z的轮廓，z的值为0，轮廓线宽为2。注意此时的z对应的范围应该与U和V所表达的范围相同。因为contour函数是用来等高线，而本实验中只需画一条等高线，所以第4个参数里面的值都是一样的，这里为[0,0],0指的是函数值z在0和0之间的等高线(很明显，只能是一条)。

　　在logistic回归中，其表达式为：

　　

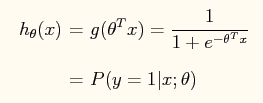
　　在此问题中，将特征x映射到一个28维的空间中，其x向量映射后为：

　　

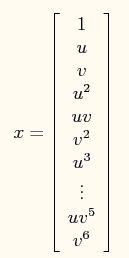
　　此时加入了规则项后的系统的损失函数为：

　　

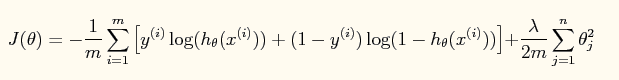
　　对应的牛顿法参数更新方程为：

　　

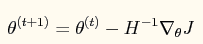
　　其中：

　　

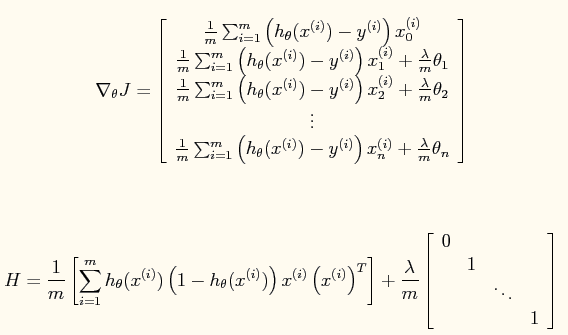
　　公式中的一些宏观说明（直接截的原网页）：

　　

　　实验结果：

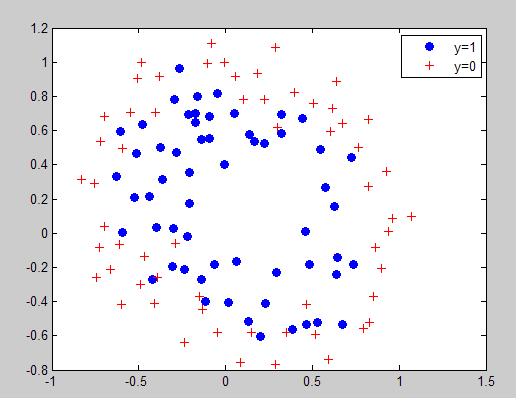
　　原训练数据点的分布情况：

　　

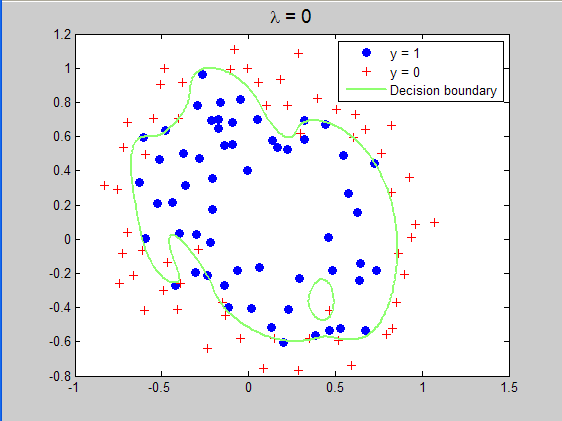
　　当lambda=0时所求得的分界曲面：

　　 

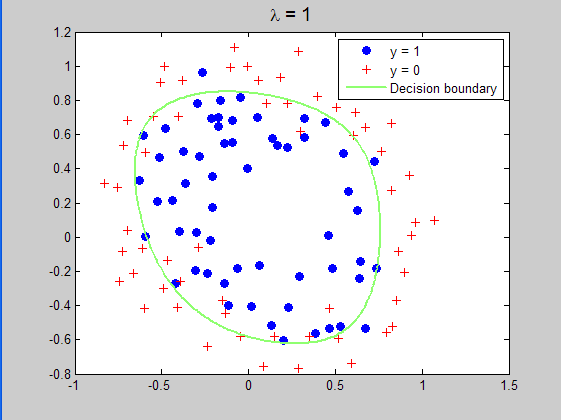
　　当lambda=1时所求得的分界曲面：

　　

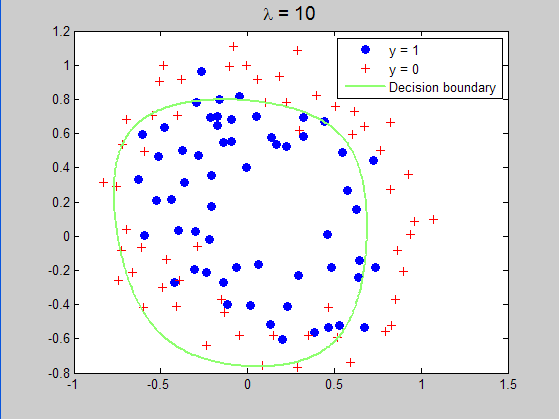
　　当lambda=10时所求得的分界曲面：

　　

　　实验程序代码：

%载入数据
clc,clear,close all;
x = load('ex5Logx.dat');
y = load('ex5Logy.dat');

%画出数据的分布图
plot(x(find(y),),x(find(y),),'o','MarkerFaceColor','b')
hold on;
plot(x(find(y==),),x(find(y==),),'r+')
legend('y=1','y=0')

% Add polynomial features to x by
% calling the feature mapping function
% provided in separate m-file
x = map_feature(x(:,), x(:,)); %map_feature函数是什么？

[m, n] = size(x);

% Initialize fitting parameters
theta = zeros(n, );

% Define the sigmoid function
g = inline('1.0 ./ (1.0 + exp(-z))'); 

% setup for Newton's method
MAX_ITR = ;
J = zeros(MAX_ITR, );

% Lambda is the regularization parameter
lambda = ;%lambda=,,，修改这个地方，运行3次可以得到3种结果。

% Newton's Method
for i = :MAX_ITR
    % Calculate the hypothesis function
    z = x * theta;
    h = g(z);

    % Calculate J (for testing convergence)
    J(i) =(/m)*sum(-y.*log(h) - (-y).*log(-h))+ ...
    (lambda/(*m))*norm(theta([:end]))^;

    % Calculate gradient and hessian.
    G = (lambda/m).*theta; G() = ; % extra term for gradient
    L = (lambda/m).*eye(n); L() = ;% extra term for Hessian
    grad = ((/m).*x' * (h-y)) + G;
    H = ((/m).*x' * diag(h) * diag(1-h) * x) + L;

    % Here is the actual update
    theta = theta - H\grad;

end
% Show J to determine if algorithm has converged
J
% display the norm of our parameters
norm_theta = norm(theta) 

% Plot the results
% We will evaluate theta*x over a
% grid of features and plot the contour
% where theta*x equals zero

% Here is the grid range
u = linspace(-, 1.5, );
v = linspace(-, 1.5, );

z = zeros(length(u), length(v));
% Evaluate z = theta*x over the grid
for i = :length(u)
    for j = :length(v)
        z(j,i) = map_feature(u(i), v(j))*theta;%这里绘制的并不是损失函数与迭代次数之间的曲线，而是线性变换后的值
    end
end
z = z'; % important to transpose z before calling contour

% Plot z =
% Notice you need to specify the range [, ]
contour(u, v, z, [, ], 'LineWidth', )%在z上画出为0值时的界面，因为为0时刚好概率为0.，符合要求
legend('y = 1', 'y = 0', 'Decision boundary')
title(sprintf('\\lambda = %g', lambda), 'FontSize', )

hold off

% Uncomment to plot J
% figure
% plot(:MAX_ITR-, J, 'o--', 'MarkerFaceColor', 'r', 'MarkerSize', )
% xlabel('Iteration'); ylabel('J')

疑问： 上文中的map_feature是什么函数？