关于SVD(Singular Value Decomposition)的那些事儿

SVD简介

SVD不仅是一个数学问题，在机器学习领域，有相当多的应用与奇异值都可以扯上关系，比如做feature reduction的PCA，做数据压缩（以图像压缩为代表）的算法，还有做搜索引擎语义层次检索的LSI（Latent Semantic Indexing）或隐性语义分析（Latent Semantic Analysis）。另外在工程应用中的很多地方都有它的身影，例如在推荐系统方面。在2006年末，电影公司Netflix曾经举办一个奖金为100万刀乐的大赛，这笔奖金会颁给比当时最好系统还要好10%的推荐系统参赛者。It is the “SVD” that the winner used。（点击可以下载相关文献）Yehuda Koren, “The BellKor Solution to the Netflix Grand Prize,” August 2009。

奇异值与特征值

关于特征值我们比较熟悉，因为在大学课程《线性代数》中就讲到了特征值与特征向量。而对于奇异值可能会比较陌生，在讲解特征值之后会详细讲解奇异值。

特征值分解和奇异值分解在机器学习领域是非常普遍的，而且两者有着密切的关系。

特征值分解

对于一个方阵A，如果一个向量v和实数λ满足如下关系：

Av = λv

则λ被称为特征向量v对应方阵A的特征值，一个矩阵的一组特征向量是一组正交向量。

令AU = U∧。其中：

U = [v1 v2 ... v_m]，

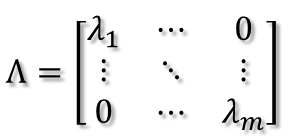
这里假设A有m个特征值，特征值分解是将一个矩阵分解成下面的形式：

A = U∧U^-1= U∧U^T

其中U是这个矩阵A的特征向量组成的矩阵，由于U是正交阵，正交阵的逆矩阵等于其转置；Σ是一个对角阵，每一个对角线上的元素就是一个特征值。

矩阵A分解了，相应的，其对应的映射也分解为三个映射。现在假设有向量x，用A将其变换到A的列空间中，那么首先由U^T先对x做变换：

U是正交阵，则U^T也是正交阵，所以U^T对x的变换是正交变换，它将x用新的坐标系来表示，这个坐标系就是A的所有正交的特征向量构成的坐标系。比如将x用A的所有特征向量表示为：

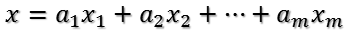
则通过第一个变换就可以把x表示为[a1 a2 ... am]^T。

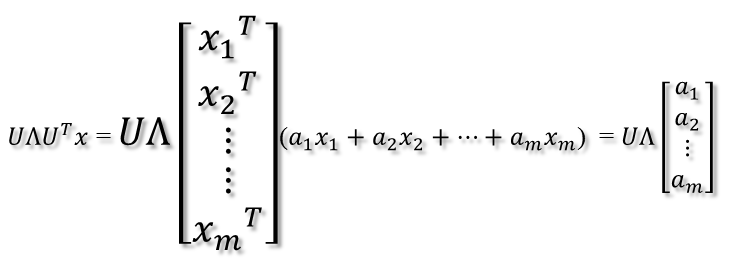
然后，在新的坐标系表示下，由中间那个对角矩阵对新的向量坐标换，其结果就是将向量往各个轴方向拉伸或压缩：

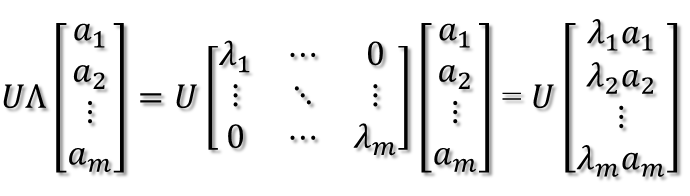
从上图可以看到，如果A不是满秩的话，那么就是说对角阵的对角线上元素存在0，这时候就会导致维度退化，这样就会使映射后的向量落入m维空间的子空间中。

最后一个变换就是U对拉伸或压缩后的向量做变换，由于U和U^-1是互为逆矩阵，所以U变换是U^-1变换的逆变换。

因此，从对称阵的分解对应的映射分解来分析一个矩阵的变换特点是非常直观的。假设对称阵特征值全为1那么显然它就是单位阵，如果对称阵的特征值有个别是0其他全是1，那么它就是一个正交投影矩阵，它将m维向量投影到它的列空间中。

特征值的几何意义

一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。例如下面的矩阵：

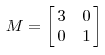
它对应的线性变换如图1所示：

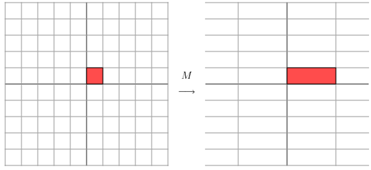
图1

相当于在x轴上较原来的向量扩展了3倍。也就是说对每一个对角线上的元素将会对一个维度进行拉伸变换，当值>1时，拉伸；当值<1时，缩短。当矩阵不是对称阵时，例如下面的矩阵M

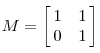它所描述的变换如图2所示：

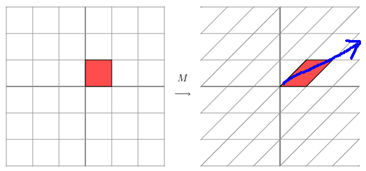
图2

这其实是在平面上对一个轴进行的拉伸变换（如蓝色的箭头所示）。在图中，蓝色的箭头是一个最主要的变化方向（变化方向可能有不止一个），如果我们想要描述好一个变换，那我们就描述好这个变换主要的变化方向就好了。反过头来看看之前特征值分解的式子，分解得到的Σ矩阵是一个对角阵，里面的特征值是由大到小排列的，这些特征值所对应的特征向量就是描述这个矩阵变化方向（从主要的变化到次要的变化排列）

当矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换。这个线性变化可能没法通过图片来表示，但是可以想象，这个变换也同样有很多的变换方向。我们通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向，就可以近似这个矩阵（变换）。也就是说：提取这个矩阵最重要的特征。总结一下，特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。不过，特征值分解一个最大的局限就是变换的矩阵必须是方阵。

奇异值分解

特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的。在现实的世界中，我们看到的大部分矩阵都不是方阵，比如说有N个学生，每个学生有M科成绩，这样形成的一个NxM的矩阵就不可能是方阵，我们怎样才能描述这样普通的矩阵呢的重要特征呢？奇异值分解可以用来干这个事情，奇异值分解是一个能适用于任意的矩阵的一种分解的方法：

A = UΣV^T

假设A是一个N * M的矩阵，那么得到的U是一个NxN的方阵（里面的向量是正交的，U里面的向量称为左奇异向量），Σ是一个NxM的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），V’(V的转置)是一个NxN的矩阵，里面的向量也是正交的，V里面的向量称为右奇异向量），如图3所示：

图3

奇异值与特征值的关系

现在假设存在M*N矩阵A，事实上，A矩阵将n维空间中的向量映射到k（k<=m）维空间中，k=rank(A)。现在的目标就是：在n维空间中找一组正交基，使得经过A变换后还是正交的。假设已经找到这样一组正交基：

则A矩阵将这组基映射为：

并满足如下关系：

所以如果正交基v选择为A^TA的特征向量的话，由于A^TA是对称阵（N * M），v之间两两正交，那么

将A^TA看做一个N*M的矩阵。

因为

所以

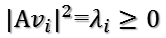
所以取单位向量

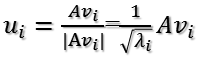
由此可得

当k < i <= m时，对u₁,u₂,...,u_k进行扩展u_k+1,...,u_m，使得u₁,u₂,...,u_m为m维空间中的一组正交基，即将{u₁,u₂,...,u_k}正交基扩展成{u₁,u₂,...,u_m}，R^m空间的单位正交基。

同样的，对v₁,v₂,...,v_k进行扩展v_k+1,...,v_n（这n-k个向量存在于A的零空间中，即Ax=0的解空间的基），使得v₁,v₂,...,v_n为n维空间中的一组正交基，即在A的零空间中选取{v_k+1,v_k+2,...,v_n}，使得Av_i = 0，i > k，并取。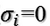

则可得到

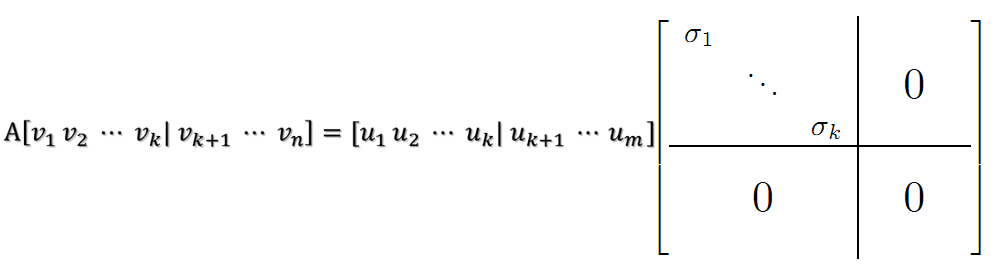
继而可以得到A矩阵的奇异值分解：

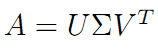
这里的u就是左奇异向量，V^T就是右奇异向量。奇异值σ跟特征值类似，在矩阵Σ中也是从大到小排列，而且σ的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们也可以用前r大的奇异值来近似描述矩阵，这里定义一下部分奇异值分解：

r是一个远小于m、n的数，这样就可以进行压缩矩阵。例如：m、n取32，r取2，那么相对于A所占空间大小1024，U、Σ、V^T总共的空间大小为（64+64+2 = 130），获得了几乎10倍的压缩比。

SVD证明满秩分解

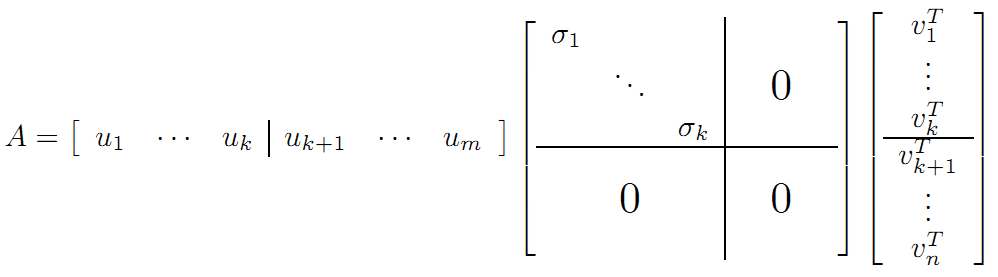
利用矩阵分块乘法展开得：

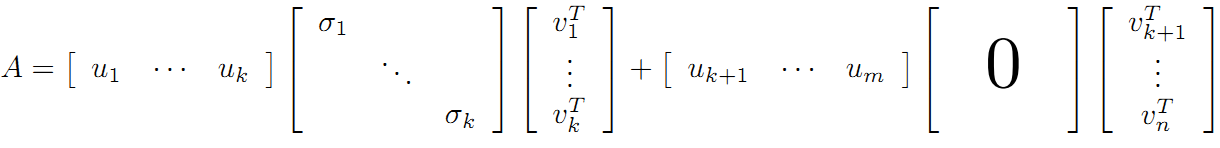
可以看到第二项为0，有

令

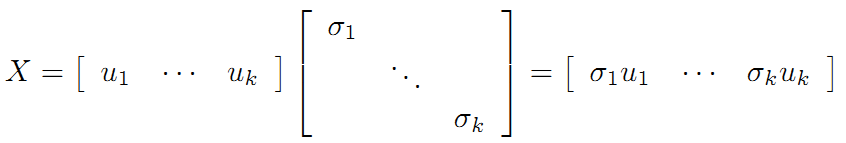
则A=XY即是A的满秩分解。

如何选取需要保留的奇异值

一个典型的做法就是保留矩阵中90%的能量信息：将所有的奇异值求其平方和，将奇异值的平方和累加到总值的90%为止。后边会给出一个具体的应用例子。另一个启发式策略就是：当矩阵有上万个奇异值时，那么就保留前面的2000或3000个。

例如矩阵M，如下所示：

 M = [[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
      [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
　　　 [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
      [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
      [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
      [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
      [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
      [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
      [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
      [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
      [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]

我们利用numpy库中的svd方法对M做奇异值分解，过程如下：

1、获得分解后的矩阵U、Sigma、VT，即M = U * Sigma * VT。

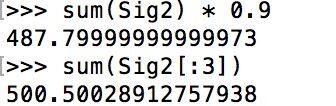
2、计算矩阵的总能量

并求出其90%的能量数值，最终可以看出前三个元素所包含的能量就高于总能量的90%。

关于SVD的应用在此不做详细介绍，本篇文章只是对SVD有个大概的认识和理解，具体的算法会在以后的文章中专门给出。

参考资料

Dan Kalman, A Singularly Valuable Decomposition: The SVD of a Matrix, The College Mathematics Journal 27 (1996), 2-23.

机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用

Peter Harrington，Machine Learning in Action（机器学习实战）