有一个容量为n的背包，有1, 2, 3, ..., n这n种物品，每种物品可以无限使用，求装满的方案数。

法一:

http://mathworld.wolfram.com/PartitionFunctionP.html:

Euler invented a generating function which gives rise to a recurrence equation in ,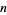

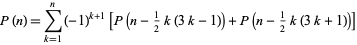法二：

背包求解

大小 < sqrt(n) 的物品，只有sqrt(n)种，用普通的完全背包可以在O(n ** 1.5)的时间复杂度内解决。

大小 >= sqrt(n) 的物品，只会选sqrt(n)个，设k = sqrt(n), f[i][j]表示选了i个物品，和为j的方案

则f[i][j] = f[i-1][j-k] + f[i][j-i]（第一种是加入了一个大小为k的物品，第二种是所有物品重量+1）

这种方法常数略大（是我写得丑吗）

the partition number的更多相关文章

  1. PARTITION(number theory) ALSO Explosive number in codewars

    问题出于codewars,简言之:寻找和为一个整数的的不同整数组合.https://en.wikipedia.org/wiki/Partition_(number_theory) 例如:和为6的整数组 ...

  2. Partition：Partiton Scheme是否指定Next Used？

    在SQL Server中,为Partition Scheme多次指定Next Used,不会出错,最后一次指定的FileGroup是Partition Scheme的Next Used,建议,在执行P ...

  3. Partition：分区切换（Switch）

    在SQL Server中,对超级大表做数据归档,使用select和delete命令是十分耗费CPU时间和Disk空间的,SQL Server必须记录相应数量的事务日志,而使用switch操作归档分区表 ...

  4. You cannot change a partition into an extended one or vice versa Delete it first

    在Linux扩展LVM时,使用fdisk创建分区时,在磁盘上新建扩展分区(逻辑分区),修改分区格式,指定分区类型为8e时,报错"You cannot change a partition i ...

  5. 磁盘、分区及Linux文件系统 [Disk, Partition, Linux File System]

    1.磁盘基础知识 1.1 物理结构 硬盘的物理结构一般由磁头与碟片.电动机.主控芯片与排线等部件组成:当主电动机带动碟片旋转时,副电动机带动一组(磁头)到相对应的碟片上并确定读取正面还是反面的碟面,磁 ...

  6. LVM XFS增加硬盘分区容量(resize2fs: Bad magic number in super-block while)

    LVM XFS增加硬盘分区容量(resize2fs: Bad magic number -- :: 分类: Linux LVM XFS增加硬盘分区容量(resize2fs: Bad magic num ...

  7. From Disk partition to PostgreSQL installation

    From Disk partition to PostgreSQLinstallation [root@compute mnt]# fdisk /dev/sdb Welcome to fdisk (u ...

  8. Creating a Swap Partition

    Creating a Swap Partition 1.   Use  fdisk /dev/vda  to open your disk in fdisk. (Use gdisk if you ar ...

  9. MySQL 分区表 partition线上修改分区字段，后续进一步学习partition (1)

    公司线上在用partition,有一个表的分区字段错了,需要重建,结果发现没有办法像修改主键字段或者修改索引字段那样直接一条sql搞定.而是需要建临时表,有down time,所以去仔细看了文档,研究 ...

随机推荐

  1. 一天学完UFLDL

    学习UFLDL笔记 第一节 神经网络 神经元长这样 大写W看着有点不习惯.. 激活函数, 就是上面式子中的f. 可以选 sigmoid函数(或者叫 logistic回归,对数几率函数),反正就是这样一 ...

  2. prime，素数的判断——c语言

    输入一个数a,求他是否是素数(用函数) 程序: #include<stdio.h> int prime(int a)-----------------------------------/ ...

  3. JavaScript 输入自动完成插件

    作为web开发的一员,应该都不陌生,信息处理时,很多时候需要根据用户的输入实时反馈查询结果供其选择,这给了用户很好的人机交互体验,在各大门户网站上已经被使用的很成熟了,最近项目中用到此功能,网上有很多 ...

  4. 【小结】有关mysql扩展库和mysqli扩展库的crud操作封装

    现阶段php如果要操作mysql数据库 php给我们提供了3套库 1.mysql扩展库   面向过程操作 2.mysqli扩展库  面向对象操作和面向过程操作并存  安全性和效率高于mysql扩展库 ...

  5. 或许有一两点你不知的C语言特性

    关键字篇 volatile关键字 鲜为人知的关键字之一volatile,表示变量是'易变的',之所以会有这个关键字,主要是消除编译优化带来的一些问题,看下面的代码 ; int b = a; int c ...

  6. TicTacToe井字棋 by reinforcement learning

    对于初学强化学习的同学,数学公式也看不太懂, 一定希望有一些简单明了的代码实现加强对入门强化学习的直觉认识,这是一篇初级入门代码, 希望能对你们开始学习强化学习起到基本的作用. 井字棋具体玩法参考百度 ...

  7. python for list generate content

    content = [ii for ii in range(50)] This can generate a list content

  8. java 读入换行

    java中实现换行有以下几种方法:1.使用java中的转义符"\r\n": 注意:\r,\n的顺序是不能够对换的,否则不能实现换行的效果． 2.BufferedWriter的new ...

  9. dp 0-1背包问题

    0-1背包的状态转换方程 f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ),  f[i-1,j] } f[i,j]表示在前i件物品中选择若干件放在承重为 j 的背包 ...

  10. 如何启用Service，如何停用Service

    一．步骤 第一步:继承Service类 public class SMSService extends Service { } 第二步:在AndroidManifest.xml文件中的<appl ...