快速质因数分解及素性测试&ABC142D

首先，这个整数的标准分解非常的显然易见对吧：

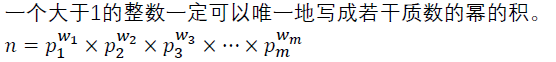
一般我们要把一个数分解成这个样子我们可以这样写：

 #include<cstdio>
 int p[],w[],k;
 void factorize(int n)
 {
     for(int i=;i*i<=n;i++)
         if(n%i==)
         {
             p[++k]=i;
             while(n%i==)
                 n/=i,w[k]++;
         }
     if(n!=)
         p[++k]=n,w[k]=;
 }
 int main()
 {
     int n;
     scanf("%d",&n);
     factorize(n);
     for(int i=;i<k;i++)
         printf("%d^%d*",p[i],w[i]);
     printf("%d^%d",p[k],w[k]);
 }

由于是分解质数，而且质数除了2之外都是奇数，所以可以在枚举i的时候每次i+=2

例题：ABC142D（手边没有什么好题了，只是因为最近做到了它2333）

要找互质的公因数，就相当于找最大公因数的最多互质的因数。（这个表述...相信你们能懂

之前写一直T了，于是找了另外一种方法，后面才发现之前的哪里有问题

 #include<cstdio>
 #include<algorithm>
 #include<map>
 using namespace std;
 #define N 100005
 #define ll long long
 #define MOD 1000000007
 ll x,y;
 map<ll,bool> vis;
 ll p[N];
 int pn;
 ll gcd(ll a,ll b)
 {
     if(b==) return a;
     else return gcd(b,a%b);
 }
 int main()
 {
     scanf("%lld %lld",&x,&y);
     ll d=gcd(x,y);
     int ans=;
     if(d%==) ans++;
     while(d%==)
         d/=;
     for(ll i=;i*i<=d;i+=)//写成i<=d/i就可以不开ll 否则不开ll就会乘爆 然后T掉
         if(d%i==)
         {
             ans++;
             while(d%i==)
                 d/=i;
         }
     if(d!=) ans++;
     printf("%d\n",ans);
     return ;
 }

就是我注释的那个地方，要注意那样的BUG了

最后采用了这种写法：

 #include<cstdio>
 #include<algorithm>
 #include<map>
 #include<vector>
 #include<cmath>
 using namespace std;
 #define N 100005
 #define ll long long
 #define MOD 1000000007
 ll x,y;
 map<ll,bool> vis;
 ll p[N];
 int pn;
 vector<ll>st;
 ll gcd(ll a,ll b)
 {
     if(b==) return a;
     else return gcd(b,a%b);
 }
 bool is_prime(ll x)
 {
     if(x==) return ;
     if(x==||x==) return ;
     if(x%!=&&x%!=) return ;
     int s=sqrt(x);
     for(int i=;i<=s;i+=)
         if(x%i==||x%(i+)==)
             return ;
     return ;
 }
 int solve(ll n)
 {
     int ans=;
     if(n==) return ;
     ll i=;
     while(i<n)
     {
         if(is_prime(n))
         {
             st.push_back(n);
             if(vis[n]==)ans++;
             vis[n]=;
             return ans;
         }
         for(int i=;i<n;i++)
         {
             if(n%i==)
             {
                 st.push_back(i);
                 if(vis[i]==)ans++;
                 vis[i]=;
                 n/=i;
                 break;
             }
         }
     }
     st.push_back(n);
     if(vis[n]==)ans++;
     vis[n]=;
     return ans;
 }
 int main()
 {
     scanf("%lld %lld",&x,&y);
     ll d=gcd(x,y);
     printf("%d\n",solve(d));
     return ;
 }

其实感觉和上面的做法差不多，直接看也就能看懂，但是网上据说是$n^{1/4}$的复杂度，那么还是了解一下，也没有什么坏处。（对于这道题来说其实不需要存因数的啦）

关于is_prime的素数判断，还是说一下吧。

如果不加这个判断，那么在$n$变成一个很大的质数的时候，这个算法就会退化到$O(n)$级别。

对于每一个$>=5$的数可以表示为$6x-1$（也相当于$6x+5$）,$6x$,$6x+1$,$6x+2$,$6x+3$,$6x+4$,$6x+5$中的一种。

而$6x$,$6x+2=2(3x+1)$,$6x+3=3(x+1)$,$6x+4=2(3x+2)$，都不可能是素数。

所以我们对于一个数n，直接先判断它模$6$是否余$5$或余$1$，不是的话直接返回false

但是是的话也不一定是素数，还要再判断一下。

每个数都能进行质因数分解，所以我们只要判断用它除前面的素数能否除尽就可以了.

$6x+1$,$6x+5$这样的数显然不可能除的尽$2$和$3$，所以我们从$5$开始判断。

下一个除以$7$，按照上面的讨论，下一个为$11$和$13$。

网上有人说，以此类推，可以把步长增加到$6$来加快运行速度。

不知道怎么证明，但是验证了一下是对的。（怎么感觉好水...）

update2019.10.9 关于把步长增加到$6$

发现自己好傻啊

前面已经说了，3以后的质数都是除以6余1或者5的数

那么连续的两个质数差为2

当然，除以6余1或者5的数不一定都是质数，不过这没有关系，我们不一定要让除数是一个质数。

---

莫名其妙地就干完了这篇博客。

写得好水呀。

嘤嘤嘤我在干什么。