【洛谷P1310 表达式的值】

题目链接

题目描述

对于1 位二进制变量定义两种运算：

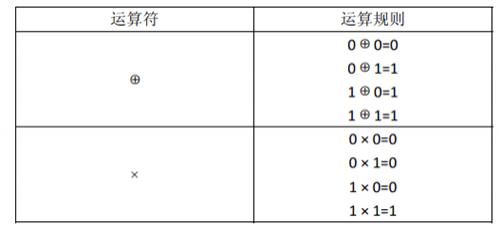
运算的优先级是：

先计算括号内的，再计算括号外的。
“× ”运算优先于“⊕”运算，即计算表达式时，先计算× 运算，再计算⊕运算。例如：计算表达式A⊕B × C时，先计算 B × C，其结果再与 A 做⊕运算。

现给定一个未完成的表达式，例如_+(_*_)，请你在横线处填入数字00或者11 ，请问有多少种填法可以使得表达式的值为00。

输入输出格式

输入格式：

共 2 行。

第1 行为一个整数 LL，表示给定的表达式中除去横线外的运算符和括号的个数。

第2 行为一个字符串包含 LL 个字符，其中只包含’（’、’）’、’+’、’*’这44 种字符，其中’（’、’）’是左右括号，’+’、’*’分别表示前面定义的运算符“⊕”和“×”。这行字符按顺序给出了给定表达式中除去变量外的运算符和括号。

输出格式：

共1 行。包含一个整数，即所有的方案数。注意：这个数可能会很大，请输出方案数对1000710007取模后的结果。

输入输出样例

输入样例#1：复制

4
+(*)

输出样例#1：复制

３

说明

【输入输出样例说明】

给定的表达式包括横线字符之后为：_+(_*_)

在横线位置填入(0 、0 、0) 、(0 、1 、0) 、(0 、0 、1) 时，表达式的值均为0 ，所以共有3种填法。

【数据范围】

对于20\%20% 的数据有0 ≤ L ≤ 100≤L≤10。

对于50\%50% 的数据有 0 ≤ L ≤ 1,0000≤L≤1,000。

对于70\%70% 的数据有0 ≤ L ≤ 10,0000≤L≤10,000 。

对于100\%100%的数据有0 ≤ L ≤ 100,0000≤L≤100,000。

对于50\%50% 的数据输入表达式中不含括号。

就是一个十分有趣恶心的堆栈题

这里显然运用到了位运算（ex的东西）

运用堆栈，遇见*和（就入栈，遇见）就将（与）之间的符号出栈，遇见+就将前面的*出栈

以此来模拟（其中‘n’表示一个未知的数值）

直到最后算完表达式，输出为0的方案数

#include<bits/stdc++.h>
using namespace std;
inline void read(int &num)
{
    bool flag=;
    num=;
    char c=getchar();
    while((c<''||c>'')&&c!='-')
    {
        c=getchar();
    }
    if(c=='-')
    {
        flag=;
        c=getchar();
    }
    num=c-'';
    c=getchar();
    while(c>=''&&c<='')
    {
        num=(num<<)+(num<<)+c-'';
        c = getchar();
    }
    if(flag)
    {
        num*=-;
    }
}
inline void output(int num)
{
    if(num<)
    {
        putchar('-');
        num=-num;
    }
    if(num>=)
    {
        output(num/);
    }
    putchar(num%+'');
}
inline void outln(int num)
{
    output(num);
}
inline void outln(string str)
{
    puts(str.c_str());
}
const int mod=;
const int N=;
int n;
char str[N];//输入的中缀表达式
stack<char> sta;//转后缀表达式时使用的栈
string final;//后缀表达式（答案序列）
stack<int> zero, one;//zero维护使表达式值为0的方案个数，one维护使表达式值为1的方案个数
int main()
{
    read(n);
    scanf("%s",str + );
    final.push_back('n');//后缀表达式最开始应该有一个未知变量
    for(int i=;i<=n;i++)
    {
        if(str[i]=='('||str[i]=='*')//遇到左括号或乘号，入栈
        {
            sta.push(str[i]);
        }
        if(str[i]=='+')//遇到加号，弹出栈顶的乘号，然后加号入栈
        {
            while(!sta.empty()&&sta.top()=='*')
            {
                final.push_back(sta.top());
                sta.pop();
            }
            sta.push(str[i]);
        }
        if(str[i]==')')//右括号，把到上一个左括号的元素出栈放入答案序列
        {
            while(sta.top()!='(')
            {
                final.push_back(sta.top());
                sta.pop();
            }
            sta.pop();
        }
        if(str[i]!='('&&str[i]!=')')//当不是左括号或者右括号时，应该插入一个未知变量
        {
            final.push_back('n');
        }
    }
    while(!sta.empty())//剩下的元素放入答案序列
    {
        final.push_back(sta.top());
        sta.pop();
    }
    for(int i=;i<final.size();i++)
    {
        char c=final[i];
        {
            if(c=='n')//单个变量，方案数为1
            {
                one.push();
                zero.push();
            }
            else
            {
                int rone=one.top(),rzero=zero.top();//rone表示右操作数（即上文中的y）为1的方案数（即上文中的y1），rzero同理
                one.pop(),zero.pop();
                int lone=one.top(),lzero=zero.top();//同理
                one.pop();
                zero.pop();
                if(c == '*')//与操作，为1需要都为1，为0需要不都为1
                {
                    one.push(lone*rone%mod);
                    zero.push((lone*rzero%mod+lzero*rone%mod+lzero*rzero%mod)%mod);
                }
                else//或操作，为0需要都为0，为1需要不都为0
                {
                    zero.push(lzero*rzero%mod);
                    one.push((lone*rzero%mod+lzero*rone%mod+lone*rone%mod)%mod);
                }
            }
        }
    }
    outln(zero.top());//需要整个表达式的值为0
    return ;
}