用R做逻辑回归之汽车贷款违约模型

• 数据说明

本数据是一份汽车贷款违约数据

application_id    申请者ID

account_number 账户号

bad_ind            是否违约

vehicle_year      汽车购买时间

vehicle_make     汽车制造商

bankruptcy_ind 曾经破产标识

tot_derog           五年内信用不良事件数量（比如手机欠费消号）

tot_tr                  全体账户数量

age_oldest_tr     最久账户存续时间（月）

tot_open_tr       在使用账户数量

tot_rev_debt     在使用可循环贷款帐户余额(比如信用卡欠款)
tot_rev_line       可循环贷款帐户限额(信用卡授权额度)
rev_util              可循环贷款帐户使用比例(余额/限额)
fico_score          FICO打分
purch_price       汽车购买金额(元)
msrp                  建议售价
down_pyt          分期付款的首次交款
loan_term         贷款期限(月)
loan_amt          贷款金额
ltv                      贷款金额/建议售价*100
tot_income       月均收入(元)
veh_mileage     行使历程(Mile)
used_ind           是否二手车
weight               样本权重

• 导入数据和数据清洗

accepts<-read.csv("accepts.csv")
accepts<-na.omit(accepts)
attach(accepts)

• 分类变量的相关关系

曾经破产标识与是否违约是否有关系?

table(bankruptcy_ind,bad_ind)

对于两分类变量的列联表分析，使用prettyR包中的xtab函数，并进行卡方检验

library(prettyR)
xtab(~ bankruptcy_ind + bad_ind, data=accepts, chisq = TRUE)

• 逻辑回归

随机抽样，建立训练集与测试集

set.seed()
select<-sample(:nrow(accepts),length(accepts$application_id)*0.7)
train=accepts[select,]
test=accepts[-select,]
attach(train)

R中的logit回归

lg<-glm(bad_ind ~fico_score+bankruptcy_ind+tot_derog+age_oldest_tr+rev_util+ltv+veh_mileage,family=binomial(link='logit'))
summary(lg)
lg_ms<-step(lg,direction = "both")
summary(lg_ms)

生成预测概率

train$p <- predict(lmg1,train,type = "response")
summary(train$p)
test$p<-predict(lmg1, test,type = "response") 

• 模型评估

一.ROC指标

roc曲线：接收者操作特征(receiveroperating characteristic),roc曲线上每个点反映着对同一信号刺激的感受性。

横轴：负正类率(false postive rate FPR)特异度，划分实例中所有负例占所有负例的比例；(1-Specificity)

纵轴：真正类率(true postive rate TPR)灵敏度，Sensitivity(正类覆盖率)

2针对一个二分类问题，将实例分成正类(postive)或者负类(negative)。但是实际中分类时，会出现四种情况.

(1)若一个实例是正类并且被预测为正类，即为真正类(True Postive TP)

(2)若一个实例是正类，但是被预测成为负类，即为假负类(False Negative FN)

(3)若一个实例是负类，但是被预测成为正类，即为假正类(False Postive FP)

(4)若一个实例是负类，但是被预测成为负类，即为真负类(True Negative TN)

TP:正确的肯定数目

FN:漏报，没有找到正确匹配的数目

FP:误报，没有的匹配不正确

TN:正确拒绝的非匹配数目

由上表可得出横，纵轴的计算公式：

(1)真正类率(True Postive Rate)TPR: TP/(TP+FN),代表分类器预测的正类中实际正实例占所有正实例的比例。Sensitivity

(2)负正类率(False Postive Rate)FPR: FP/(FP+TN)，代表分类器预测的正类中实际负实例占所有负实例的比例。1-Specificity

(3)真负类率(True Negative Rate)TNR: TN/(FP+TN),代表分类器预测的负类中实际负实例占所有负实例的比例，TNR=1-FPR。Specificity

假设采用逻辑回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如0.6，概率大于等于0.6的为正类，小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。阈值最大时，对应坐标点为(0,0),阈值最小时，对应坐标点(1,1)。

如下面这幅图，(a)图中实线为ROC曲线，线上每个点对应一个阈值

横轴FPR:1-TNR,1-Specificity，FPR越大，预测正类中实际负类越多。

纵轴TPR：Sensitivity(正类覆盖率),TPR越大，预测正类中实际正类越多。

理想目标：TPR=1，FPR=0,即图中(0,1)点，故ROC曲线越靠拢(0,1)点，越偏离45度对角线越好，Sensitivity、Specificity越大效果越好。

二 如何画roc曲线

假设已经得出一系列样本被划分为正类的概率，然后按照大小排序，下图是一个示例，图中共有20个测试样本，“Class”一栏表示每个测试样本真正的标签（p表示正样本，n表示负样本），“Score”表示每个测试样本属于正样本的概率。

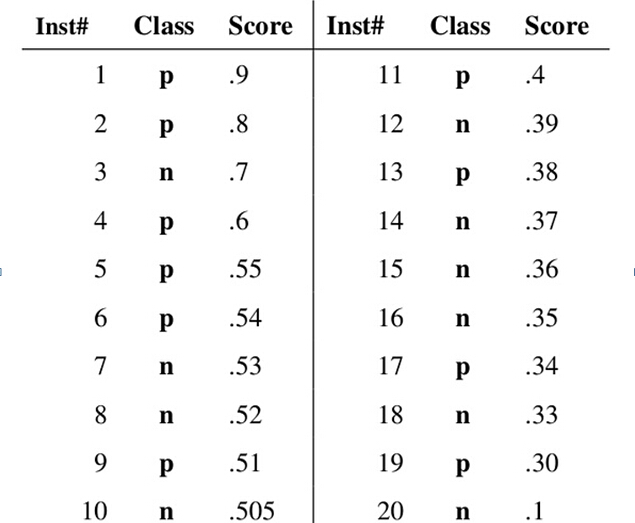
接下来，我们从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。举例来说，对于图中的第4个样本，其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本，因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本。每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值，将它们画在ROC曲线的结果如下图：

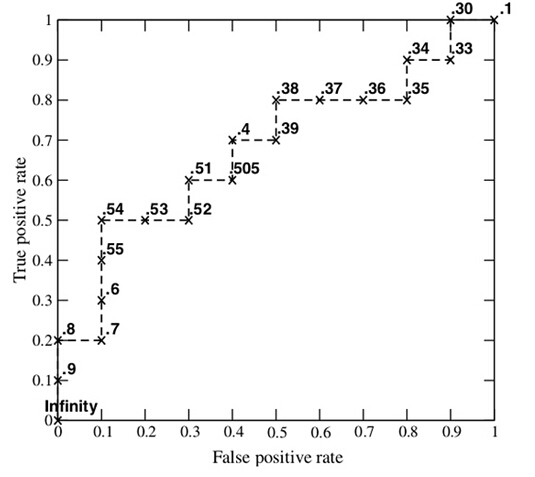
AUC(Area under Curve)：Roc曲线下的面积，介于0.1和1之间。Auc作为数值可以直观的评价分类器的好坏，值越大越好。

首先AUC值是一个概率值，当你随机挑选一个正样本以及负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值，AUC值越大，当前分类算法越有可能将正样本排在负样本前面，从而能够更好地分类。

 三.用R代码画ROC曲线

install.packages("pROC")
library(pROC)
plot.roc(bad_ind~p,train,col="")->r1
rocobjtr<- roc(train$bad_ind, train$p)
auc(rocobjtr)
lines.roc(bad_ind~p,test,col='')->r2
rocobjte <- roc(test$bad_ind, test$p)
auc(rocobjte)
roc.test(r1,r2)

自定义函数画ROC曲线，提升图，洛伦兹图，以及KS曲线

plot_roc<-function(pred,actual,data_name='data',col='black',add=FALSE,pos=c(0.7,0.2)){
  library(ROCR)
  actual<-factor(actual)
  if(length(pred)!=length(actual)){
    stop("Pred and actual must have the same length")
  }
  if(length(levels(actual))!=){
    stop("Only binary y supported")
  }
  index_set<-prediction(pred,actual)
  perf<-performance(index_set,'tpr','fpr')
  plot(perf,col=col,lty=,
       lwd=,
       add=add,
       main='ROC-Curve')
  abline(,,lty=,col='red')
  auc <- performance(index_set,"auc")@y.values[[]]
  lr_m_str<-paste0(data_name,"-AUC:",round(auc,))
  text(pos[],pos[],lr_m_str)
}

plot_lift<-function(pred,actual,data_name='data',col='black',add=FALSE,pos=c(0.8,1.5)){
  library(ROCR)
  actual<-factor(actual)
  if(length(pred)!=length(actual)){
    stop("Pred and actual must have the same length")
  }
  if(length(levels(actual))!=){
    stop("Only binary y supported")
  }
  index_set<-prediction(pred,actual)
  lift <- performance(index_set,measure='lift')@y.values[[]]
  depth <- performance(index_set,measure='rpp')@y.values[[]]
  if(add==FALSE){
    plot(depth,lift,type='l',col=col,
         lty=,lwd=,
         main='Lift-Curve')
  }
  else{
    lines(depth,lift,type='l',col=col,
          lty=,lwd=)
  }
  abline(h=,lty=,col='red')
  legend(pos[],pos[],data_name,fill=col,text.width=)
}

plot_Lorenz<-function(pred,actual,data_name='data',col='black',add=FALSE,pos=c(0.8,0.1)){
  library(ROCR)
  actual<-factor(actual)
  if(length(pred)!=length(actual)){
    stop("Pred and actual must have the same length")
  }
  if(length(levels(actual))!=){
    stop("Only binary y supported")
  }
  pred_Tr <- prediction(pred,actual)
  tpr <- performance(pred_Tr,measure='tpr')@y.values[[]]
  depth <- performance(pred_Tr,measure='rpp')@y.values[[]]
  if(add==FALSE){
    plot(depth,tpr,type='l',col=col,
         lty=,lwd=,
         main='Lorenz-Curve')
  }
  else{
    lines(depth,tpr,type='l',col=col,
          lty=,lwd=)
  }
  abline(,,lty=,col='red')
  legend(pos[],pos[],data_name,fill=col,text.width=)
}

plot_KS<-function(pred,actual,data_name='data',col='black',add=FALSE,pos=c(0.5,0.1)){
  library(ROCR)
  actual<-factor(actual)
  if(length(pred)!=length(actual)){
    stop("Pred and actual must have the same length")
  }
  if(length(levels(actual))!=){
    stop("Only binary y supported")
  }
  pred_Tr <- prediction(pred,actual)
  depth <- performance(pred_Tr,measure='rpp')@y.values[[]]
  tpr <- performance(pred_Tr,measure='tpr')@y.values[[]]
  fpr <- performance(pred_Tr,measure='fpr')@y.values[[]]
  ks<-(tpr-fpr)
  kslable<-paste0("KS:",max(ks))
  if(add==FALSE){
    plot(depth,ks,type='l',
         main='K-S-Curve',
         ylab='KS',xlab='depth')
    legend(pos[],pos[],paste0(kslable,'-',data_name),fill=col,text.width=)
  }
  else{
    lines(depth,ks,type='l',col=col,
          lty=,lwd=)
    legend(pos[],pos[],paste0(kslable,'-',data_name),fill=col,text.width=)
  }
}

thresholds<-function(pred,actual,method='best'){
  library(pROC)
  rocobjtr<- roc(actual,pred)
  thresholds<-rocobjtr$thresholds
  res<-coords(my_roc, method, ret = "threshold")
  return(res)
}

legend(0.3,0.2,paste('train:',auc(rocobjtr),sep=''),:)
legend(0.3,0.1,paste('test:',auc(rocobjte),sep=''),:)