Codeforces Round #420 (Div. 2) A,B,C

A. Okabe and Future Gadget Laboratory

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Okabe needs to renovate the Future Gadget Laboratory after he tried doing some crazy experiments! The lab is represented as an n by nsquare grid of integers. A good lab is defined as a lab in which every number not equal to 1 can be expressed as the sum of a number in the same row and a number in the same column. In other words, for every x, y such that 1 ≤ x, y ≤ n and ax, y ≠ 1, there should exist two indices s and t so that ax, y = ax, s + at, y, where ai, j denotes the integer in i-th row and j-th column.

Help Okabe determine whether a given lab is good!

Input

The first line of input contains the integer n (1 ≤ n ≤ 50) — the size of the lab.

The next n lines contain n space-separated integers denoting a row of the grid. The j-th integer in the i-th row is ai, j (1 ≤ ai, j ≤ 105).

Output

Print "Yes" if the given lab is good and "No" otherwise.

You can output each letter in upper or lower case.

Examples

input

3
1 1 2
2 3 1
6 4 1

output

Yes

input

3
1 5 2
1 1 1
1 2 3

output

No

Note

In the first sample test, the 6 in the bottom left corner is valid because it is the sum of the 2 above it and the 4 on the right. The same holds for every number not equal to 1 in this table, so the answer is "Yes".

In the second sample test, the 5 cannot be formed as the sum of an integer in the same row and an integer in the same column. Thus the answer is "No".

题意：

懒得说。

思路：

四重循环暴力；

实现代码：

#include<iostream>
using namespace std;

int main(){
    int m,i,j,k,l,a[][];
   cin>>m;
   for(i=;i<m;i++){
    for(j=;j<m;j++){
        cin>>a[i][j];
    }
   }
    int  flag = ;
   for(i=;i<m;i++){
    for(j=;j<m;j++){
        if(a[i][j]!=){
            flag  = ;
            for(k=;k<m;k++){
                for(l=;l<m;l++){
                    if(a[i][k]+a[l][j]==a[i][j])
                        flag = ;
                }
            }
            if(flag==){
                cout<<"No"<<endl;
                return ;
            }
        }
    }
   }
   cout<<"Yes"<<endl;
   return ;

}

B. Okabe and Banana Trees

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Okabe needs bananas for one of his experiments for some strange reason. So he decides to go to the forest and cut banana trees.

Consider the point (x, y) in the 2D plane such that x and y are integers and 0 ≤ x, y. There is a tree in such a point, and it has x + ybananas. There are no trees nor bananas in other points. Now, Okabe draws a line with equation 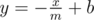. Okabe can select a single rectangle with axis aligned sides with all points on or under the line and cut all the trees in all points that are inside or on the border of this rectangle and take their bananas. Okabe's rectangle can be degenerate; that is, it can be a line segment or even a point.

Help Okabe and find the maximum number of bananas he can get if he chooses the rectangle wisely.

Okabe is sure that the answer does not exceed 1018. You can trust him.

Input

The first line of input contains two space-separated integers m and b (1 ≤ m ≤ 1000, 1 ≤ b ≤ 10000).

Output

Print the maximum number of bananas Okabe can get from the trees he cuts.

Examples

input

1 5

output

30

input

2 3

output

25

Note

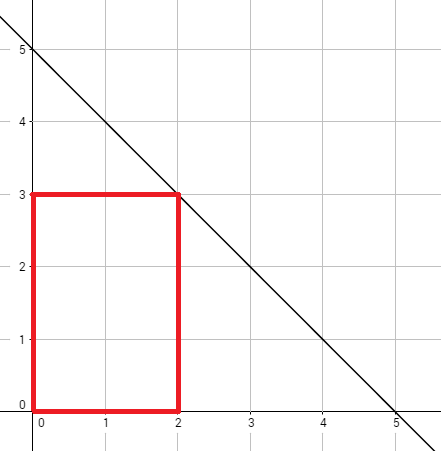
The graph above corresponds to sample test 1. The optimal rectangle is shown in red and has 30 bananas.

思路：

推公式。

实现代码：

#include<iostream>
using namespace std;
#define ll long long
ll m,b;
ll num(ll x){
   ll sum1 = ;
   //cout<<"x:"<<x<<endl;
   sum1 = (b-x/m)*(b-x/m+)/*(x+)+(b-x/m+)*(+x)*x/;
   return sum1;
}
int main(){
    ll sum=,maxx,i,j;
   cin>>m>>b;
   ll k = -m;
   ll maxn = -;
   while(k<=m*b){
        k+=m;
    if(num(k)>maxn){
        maxn = num(k);
   }
   }
   cout<<maxn<<endl;
   return ;
}

C. Okabe and Boxes

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Okabe and Super Hacker Daru are stacking and removing boxes. There are n boxes numbered from 1 to n. Initially there are no boxes on the stack.

Okabe, being a control freak, gives Daru 2n commands: n of which are to add a box to the top of the stack, and n of which are to remove a box from the top of the stack and throw it in the trash. Okabe wants Daru to throw away the boxes in the order from 1 to n. Of course, this means that it might be impossible for Daru to perform some of Okabe's remove commands, because the required box is not on the top of the stack.

That's why Daru can decide to wait until Okabe looks away and then reorder the boxes in the stack in any way he wants. He can do it at any point of time between Okabe's commands, but he can't add or remove boxes while he does it.

Tell Daru the minimum number of times he needs to reorder the boxes so that he can successfully complete all of Okabe's commands. It is guaranteed that every box is added before it is required to be removed.

Input

The first line of input contains the integer n (1 ≤ n ≤ 3·105) — the number of boxes.

Each of the next 2n lines of input starts with a string "add" or "remove". If the line starts with the "add", an integer x (1 ≤ x ≤ n) follows, indicating that Daru should add the box with number x to the top of the stack.

It is guaranteed that exactly n lines contain "add" operations, all the boxes added are distinct, and n lines contain "remove" operations. It is also guaranteed that a box is always added before it is required to be removed.

Output

Print the minimum number of times Daru needs to reorder the boxes to successfully complete all of Okabe's commands.

Examples

input

3
add 1
remove
add 2
add 3
remove
remove

output

1

input

7
add 3
add 2
add 1
remove
add 4
remove
remove
remove
add 6
add 7
add 5
remove
remove
remove

output

2

Note

In the first sample, Daru should reorder the boxes after adding box 3 to the stack.

In the second sample, Daru should reorder the boxes after adding box 4 and box 7 to the stack.

解题思路：

要按顺序输出1-n，那么当栈顶元素和当前要输出的相同时，直接输出就行，不同时，则需要进行排序操作，默认最优排序使栈中所有元素都可以按指定顺序输出，记一次操作，问需要几次操作。

实现代码：

#include<bits/stdc++.h>
using namespace std;
stack<int>sta;
int main()
{
    int m,i,x,ans = ;
    int sum = ;
    char s[];
    scanf("%d",&m);
    for(i=;i<m*;i++){
        scanf("%s",s);
        if(s[]=='a'){
            scanf("%d",&x);
            sta.push(x);
        }
        else{
                ans ++;
            if(sta.empty()==)
                continue;
            if(sta.top()!=ans){
                    sum++;
                while(sta.empty()==){
                sta.pop();}
            }
            else{
                sta.pop();
            }
        }
    }
    printf("%d\n",sum);
    return ;
}