【SCOI 2010】传送带

为了方便，我们不妨设$\rm P \lt Q,R$

我们发现，有$\rm E$点在$\rm AB$上，$\rm F$点在$\rm CD$上，最优解一定是$\rm AE\rightarrow EF\rightarrow FD$，因为若中途离开某个传送带再回来，显然是不优的。

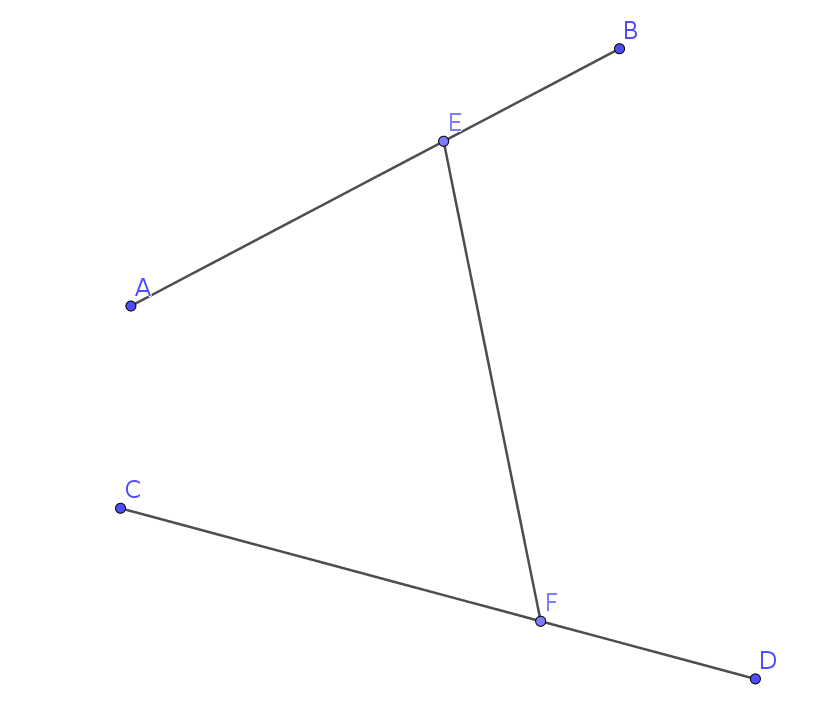
考虑固定点$E$，观察点$F$对答案造成的影响。

作过点$\rm E$作$\rm EG \perp CD$。

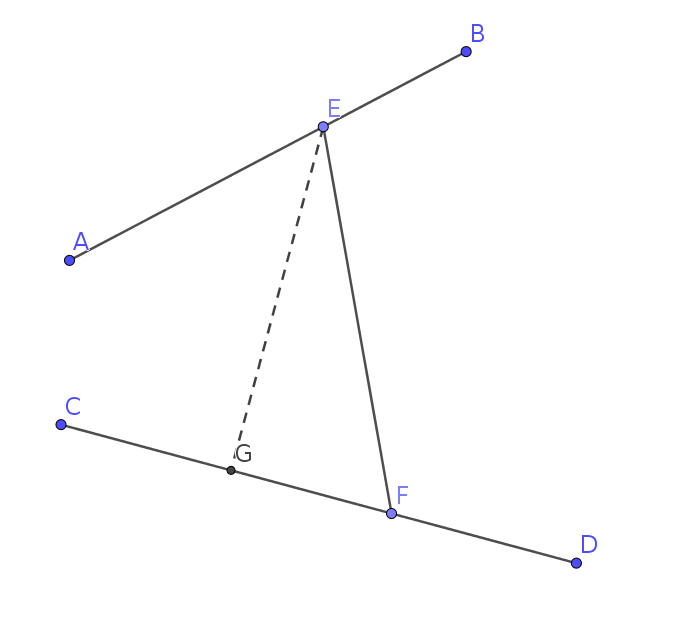
若$\rm F$在$\rm CG$上，单调性很显然。

若$\rm F$在$\rm GD$上，朝$\rm D$移动时。

　　由于$\rm |FD|$在减少，而$\rm |EF|$在增加，且越增加越快，所以$\rm |FD| + |EF|$会先减少，后增加。

所以当$\rm E$点固定的时候，$\rm AE\rightarrow EF\rightarrow FD$的长度是个凹的单峰函数，我们可以用三分解决。

我们可以先三分$E$，再三分$F$来解决这题。什么？证明？我真的不会。

至于三分的时候怎么选坐标，可以按照端点横坐标纵坐标直接取$\frac{1}{3}$。

比如下图我们要找到$\rm CB$的$\frac{1}{3}$处，直接是$\rm B$和$\rm C$横坐标纵坐标分别三分之一即可。

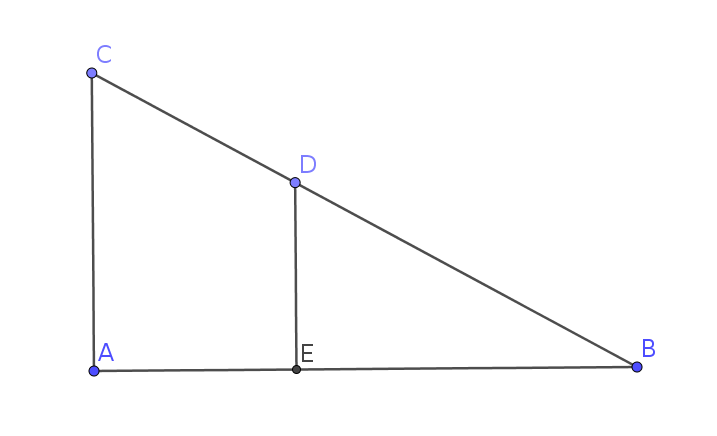
明显有$\rm \triangle ABC\sim \triangle BDE$

所以$\rm D$点也在线段的$\frac{1}{3}$

 #include <bits/stdc++.h>

 using namespace std;

 const double eps = 1e-;

 double x[], y[], p, q, r;

 double dist(double xa, double ya, double xb, double yb) {
     return sqrt((xa - xb) * (xa - xb) + (ya - yb) * (ya - yb));
 }

 double check(double ex, double ey) {
     double lx = x[], ly = y[], rx = x[], ry = y[];
     while(fabs(rx - lx) > eps || fabs(ry - ly) > eps) {
         double m1x = lx + (rx - lx) / , m1y = ly + (ry - ly) / ,
                m2x = rx - (rx - lx) / , m2y = ry - (ry - ly) / ;
         if(dist(ex, ey, m1x, m1y) / r + dist(m1x, m1y, x[], y[]) / q <
            dist(ex, ey, m2x, m2y) / r + dist(m2x, m2y, x[], y[]) / q)
             rx = m2x, ry = m2y;
         else lx = m1x, ly = m1y;
     }
     return dist(ex, ey, lx, ly) / r + dist(lx, ly, x[], y[]) / q;
 }

 int main() {
     for(int i = ; i < ; i++) cin >> x[i] >> y[i];
     cin >> p >> q >> r;
     double lx = x[], ly = y[], rx = x[], ry = y[];
     while(fabs(rx - lx) > eps || fabs(ry - ly) > eps) {
         double m1x = lx + (rx - lx) / , m1y = ly + (ry - ly) / ,
                m2x = rx - (rx - lx) / , m2y = ry - (ry - ly) / ;
         if(dist(x[], y[], m1x, m1y) / p + check(m1x, m1y) <
            dist(x[], y[], m2x, m2y) / p + check(m2x, m2y))
             rx = m2x, ry = m2y;
         else lx = m1x, ly = m1y;
     }
     printf("%.2lf\n", dist(x[], y[], lx, ly) / p + check(lx, ly));
     return ;
 }