P4285 [SHOI2008]汉诺塔 题解 （乱搞）

题目链接

P4285 [SHOI2008]汉诺塔

解题思路

提供一种打表新思路

先来证明一个其他题解都没有证明的结论：\(ans[i]\)是可由\(ans[i-1]\)线性递推的。

（\(ans[i]\)表示\(i\)个盘子全部移走的步数）

感谢keytoyzi神仙的神仙思路

---

首先，在最初两层移动的时候，遵循的移动顺序规则是题中所给的顺序。

在\(n\)个盘子都在\(A\)柱的时候，我们是怎么做的呢？

先把前\(n-1\)个盘子按照遵循初始顺序规则的方法移动到\(B\)或\(C\)；

再对第\(n\)个盘子进行操作；

再进行某些操作（后文会展开）；

最后所有盘子移动到\(B\)或者\(C\)。

这等价于：

每一层对应一个新规则，把前\(n-1\)层盘子看做一层，那就相当于按照这个新的规则移动一个两层的东西。

这个新规则是啥意思呢？光说理论太难以理解，上图：

---

解释一下：\(n-1\)代表前\(n-1\)个盘子，这些盘子根据初始规则可能移动到\(B\)或者\(C\)，而把他们看做一个整体后，相当于上图的遵循初始规则的移动方式，而这种新的移动方式，就是一个新的规则。

---

再来两张状态转移的图：

（单箭头表示这一步操作优先级高于另一侧）

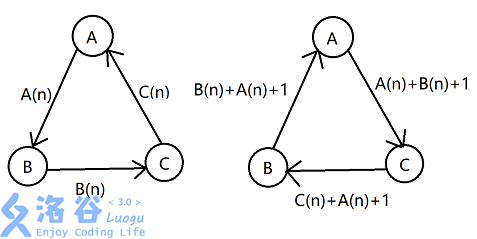
解释一下这张图。

刚开始对于前\(n\)个盘子形成的新规则：

\(AB>AC\)，\(BC>BA\)，\(CA>CB\)。

根据这个规则进行第\(n+1\)层的操作：（以\(A \to C\)为例）

先把\(A\)上的前\(n\)个盘子扔到\(B\)上；（\(A(n)\)）

再把\(A\)最底下的第\(n+1\)个盘子扔到\(C\)上；（\(1\)）

再把扔到\(B\)上的前\(n\)个盘子扔到\(C\)上。（\(B(n)\)）

故总步骤数为\(A(n)+1+B(n)\)。

同理，那么这就给出了一组递推关系。

易得，如果\(n\)满足左图，则\(n+1\)满足右图；

如果\(n\)满足右图，则\(n+1\)满足左图。

也就是说，这两张图中的状态可以互相转换。

又，\(ABC\)是等价的，故这张图对应了一种可能的答案（答案\(1\)）。

这张图更复杂一些，不过实质和刚刚的相同。

以\(A\to B\)为例。

先把\(A\)上的前\(n\)个盘子扔到\(B\)上；（\(A(n)\)）

再把\(A\)最底下的第\(n+1\)个盘子扔到\(C\)上；（\(1\)）

再把\(A\)上的这n个盘子扔回\(A\)上；（\(B(n)\)）

再把\(C\)上的第n+1个盘子扔到\(B\)上；（\(1\)）

再把\(A\)上的那\(n\)个盘子扔回\(B\)上。（\(B(n)\)）

故总步骤数为\(A(n)+1+B(n)+1+B(n)\)。

同理易得，如果n满足左图，则n+1满足右图；

如果\(n\)满足右图，则\(n+1\)满足左图。

也就是说，这两张图中的状态还是可以互相转换。

而在这张图上，\(AB\)是等价的，\(C\)是另一种情况，故这张状态图对应了两种可能的答案：

\(AB\)对应的状态为初始\(A\)柱（答案\(2\)）

或

\(C\)对应的状态为初始\(A\)柱（答案\(3\)）。

---

好，那么现在对应这三种情况做一种简单的分析。

对于第一种答案：

\(ABC\)等价，故\(A(n)=B(n)=C(n)=ans_1[n]\)

由图中的递推公式，\(ans_1[n+1]=ans_1[n]*2+1\)

对于第二种答案：

\(AB\)等价，\(A(n)=B(n)=ans_2[n]\)

\(ans_2[n+1]=ans_2[n]*3+2\)

对于第三种答案：

\(AB\)等价，\(A(n)=B(n)=ans_2[n]\)

\(ans_3[n+1]=ans_2[n]+ans_3[n]+1\)

这是一个线性表达式。

证毕。

---

所以，我们只需要知道移动一个盘子、两个盘子、三个盘子的情况，即可知道递推公式进而求解。

手动模拟打表，容易得到以下结果：

（\(ans[i]\)表示i个盘子全部移走的步数）

一个盘子：

\(ans[1]=1\)

两个盘子：

\((1)AB>AC\)

①\(BC>BA\)，\(ans[2]=3\)

②\(BC<BA\)，\(ans[2]=5\)

\((2)AB<AC\)

这里可以看做把\(BC\)柱子换了个位置

①\(ans[2]=3\)：原\(BC>BA\)，把\(BC\)换了个位置后变成\(CB>CA\)

②\(ans[2]=5\)：原\(BC<BA\)，同理变成\(CB<CA\)

三个盘子：

\((1)AB>AC\)

①\(BC>BA\)

\((i)CB>CA\)，\(ans[3]=9\)

\((ii)CB<CA\)，\(ans[3]=7\)

②\(BA>BC\)

\(ans[3]=17\)

\((2)AB<AC\)

同理，不再赘述

---

下附递推AC代码：

#include<stdio.h>
char a[4];
int seq[3][3];
long long ans[40];
int main(){
	int i,n;
	scanf("%d",&n);
	for(i=0;i<6;i++){
		scanf("%s",a);
		seq[a[0]-'A'][a[1]-'A']=6-i;
	}
	if(seq[0][1]>seq[0][2]){//AB>AC
		if(seq[1][2]<seq[1][0]){//BC<BA
			ans[2]=5;ans[3]=17;
		}else{
			if(seq[2][0]>seq[2][1]){//CA>CB
				ans[2]=3;ans[3]=7;
			}else{
				ans[2]=3;ans[3]=9;
			}
		}
	}else{//AB<AC
		if(seq[2][1]<seq[2][0]){//CB<CA
			ans[2]=5;ans[3]=17;
		}else{
			if(seq[1][0]>seq[1][2]){//BA>BC
				ans[2]=3;ans[3]=7;
			}else{
				ans[2]=3;ans[3]=9;
			}
		}
	}
	ans[1]=1;
	int b=(ans[2]*ans[2]-ans[1]*ans[3])/(ans[2]-ans[1]);
	int k=(ans[2]-b)/cnt1;
	for(i=4;i<=n;i++)ans[i]=ans[i-1]*k+b;
	printf("%lld",ans[n]);
	return 0;
}

---

其实，这已经没有必要写成递推形式了。我们在讨论三种答案的时候，其实已经可以手算算出三种情况的O(1)表达式了。

来一发最短AC代码

#include<stdio.h>
#include<math.h>
typedef long long ll;
char a[4];
int s[9],p,n,i=6;
ll f(int x){
	if(x==1)return (ll)2*pow(3,n-1)-1;
	if(x)return (ll)pow(2,n)-1;
	return (ll)pow(3,n-1);
}
int main(){
	scanf("%d",&n);
	while(i--)scanf("%s",a),s[(a[0]-'A')*3+a[1]-'A']=i;
	if(s[1]>s[2]){
		if(s[5]<s[3])p=1;
		else if(s[6]>s[7])p=2;
	}else if(s[7]<s[6])p=1;
	else if(s[3]>s[5])p=2;
	printf("%lld",f(p));
	return 0;
}