在Python里，用股票案例讲描述性统计分析方法（内容来自我的书）

描述性统计是数学统计分析里的一种方法，通过这种统计方法，能分析出数据整体状况以及数据间的关联。在这部分里，将用股票数据为样本，以matplotlib类为可视化工具，讲述描述性统计里常用指标的计算方法和含义。

1 平均数、中位数和百分位数

平均数比较好理解，是样本的和除以样本的个数。

中位数也叫中值，假设样本个数是奇数，那么数据按顺序排列后处于居中位置的数则是中位数，如果样本个数是偶数，那么排序后，中间两个数据的均值则是中位数。通俗地讲，在样本数据里，有一半的样本比中位数大，有一半比它小。

把中位数的概念扩展一下，即可得到百分位数。比如第25百分位数则表示，样本数据里，有25%的数据小于等于它，而75%的数据大于它。在实际项目里，还会把第25百分位数、中位数和第75百分位数组合起来形成四分位数，因为通过这些数，能把样本一分为四。其中第25百分位数也叫下四分位数，第75百分位数也叫上四分位数。

理解概念后，在如下的CalAvgMore.py范例中，将以股票收盘价为例，演示平均数、中位数和四分位数的求法。

1	#coding=utf-8
2	import pandas as pd
3	filename='D:\\work\\data\\ch9\\6007852019-06-012020-01-31.csv'
4	df = pd.read_csv(filename,encoding='gbk') #读取数据到DataFrame
5	print(df['Close'].mean()) #输出收盘价的平均值
6	print(df['Close'].median()) #输出收盘价的中位数
7	print(df['Close'].quantile(0.5)) #输出收盘价第50百分位数
8	print(df['Close'].quantile(0.25)) #输出收盘价第25百分位数
9	print(df['Close'].quantile(0.75)) #输出收盘价第75百分位数

在进行数据分析时，一般会先从csv文件等数据源里获取样本，获取后用表格类型的DataFrame对象来存储，所以在第3行和第4行里，演示从指定csv文件里得到数据并通过read_csv导入到DataFrame类型对象的做法，这里用到csv是由9.1.4部分的StoreStockToMySQL范例生成的。

Pandas库的DataFrame对象已经封装了求各种统计数据的方法，具体而言，能通过第5行的mean方法求平均值，在调用时，还可以用诸如df['Close']的样式，指定针对哪列数据计算。通过第6行的median方法，能计算指定列的中位数。

在第7行到第9行的代码里，是通过 quantile方法求百分位数，比如第7行的参数是0.5，则求第50的百分位数。运行本范例，能看到如下的输出结果，其中第2行输出的中位数和第3行输出的第50百分位数是一个结果。

2 用箱状图展示分位数

箱状图能以可视化的方式，形象地展示平均数和诸多分位数。在如下的BoxPlotDemo.py范例中，将还是以股票收盘价为例，展示箱状图的绘制技巧，从中大家能进一步了解分位数的概念。

1	#coding=utf-8
2	import pandas as pd
3	import matplotlib.pyplot as plt
4	filename='D:\\work\\data\\ch9\\6007852019-06-012020-01-31.csv'
5	df = pd.read_csv(filename,encoding='gbk') #读取数据到DataFrame
6	#绘制箱状图
7	df['Close'].plot.box(patch_artist=True,notch = True)
8	plt.show()

在代码的第5行里，还是通过read_csv方法把csv文件数据读到df对象，之后，是通过第7行的plot.box方法，绘制“收盘价”的箱状图，运行本范例后，能看到如下图所示的效果。

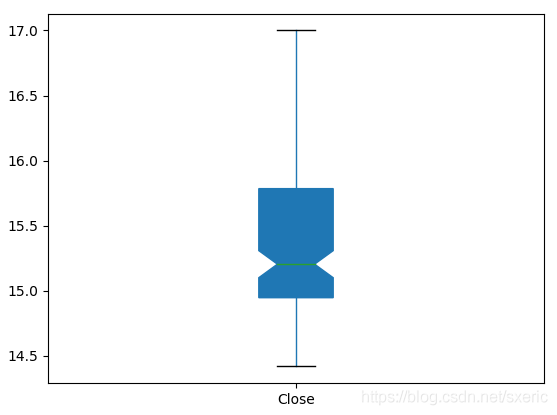
在第7行绘制箱状图时传入了两个参数，其中patch_artist=True表示需要填充箱体的颜色，用notch = True表示以凹口的方式展示箱状图。从上述箱状图里，能形象地看到最高和最低的值，以及第25、第50和第75百分位数的值，由此更能形象地看到“收盘价”样本数的聚集区间。

3 统计极差、方差和标准差

在统计学里，一般用这三个指标来衡量样本数据的离散度，即衡量样本数对于中心位置（一般是平均数）的偏离程度。

其中，极差的算法比较简单，是样本里最大值和最小值的差，而方差是每个样本值与全体样本值的平均数之差的平方值的平均数，标准差则是方差的平方根。在如下的CalAlias.py范例中，将演示这三个值的获取方式。

1	#coding=utf-8
2	import pandas as pd
3	filename='D:\\work\\data\\ch9\\6007852019-06-012020-01-31.csv'
4	df = pd.read_csv(filename,encoding='gbk') #读取数据到DataFrame
5	print(df['Close'].max() - df['Close'].min()) #求极差
6	print(df['Close'].var()) #求方差
7	print(df['Close'].std()) #求标准差

在第5行里，是通过最大值减最小值的方法算出了极差，在第6行里，通过var方法计算了方差，第7行则通过std方法求标准差。

本文出自我写的书： Python爬虫、数据分析与可视化：工具详解与案例实战，https://item.jd.com/10023983398756.html

请大家关注我的公众号：一起进步，一起挣钱，在本公众号里，会有很多精彩文章。